支持向量机系列四：Outliers

原文链接请点击这里

在最开始讨论支持向量机的时候，我们就假定，数据是线性可分的，亦即我们可以找到一个可行的超平面将数据完全分开。后来为了处理非线性数据，使用 Kernel 方法对原来的线性 SVM 进行了推广，使得非线性的的情况也能处理。虽然通过映射ϕ(⋅)将原始数据映射到高维空间之后，能够线性分隔的概率大大增加，但是对于某些情况还是很难处理。例如可能并不是因为数据本身是非线性结构的，而只是因为数据有噪音。对于这种偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support vector 里又存在 outlier 的话，其影响就很大了。例如下图：

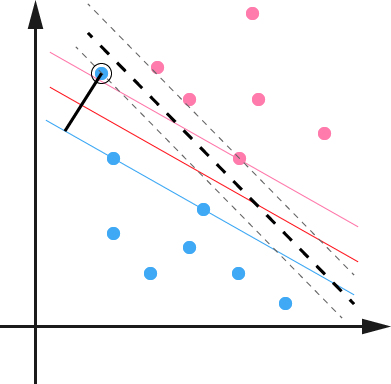
Optimal-Hyper-Plane-2

用黑圈圈起来的那个蓝点是一个 outlier ，它偏离了自己原本所应该在的那个半空间，如果直接忽略掉它的话，原来的分隔超平面还是挺好的，但是由于这个 outlier 的出现，导致分隔超平面不得不被挤歪了，变成途中黑色虚线所示（这只是一个示意图，并没有严格计算精确坐标），同时 margin 也相应变小了。当然，更严重的情况是，如果这个 outlier 再往右上移动一些距离的话，我们将无法构造出能将数据分开的超平面来。

为了处理这种情况，SVM 允许数据点在一定程度上偏离一下超平面。例如上图中，黑色实线所对应的距离，就是该 outlier 偏离的距离，如果把它移动回来，就刚好落在原来的超平面上，而不会使得超平面发生变形了。具体来说，原来的约束条件

yi(wTxi+b)≥1,i=1,…,n

yi(wTxi+b)≥1−ξi,i=1,…,n

其中ξi≥0称为松弛变量 (slack variable) ，对应数据点xi允许偏离的 functional margin 的量。当然，如果我们允许ξi任意大的话，那任意的超平面都是符合条件的了。所以，我们在原来的目标函数后面加上一项，使得这些ξi的总和也要最小：

min12‖

其中C是一个参数，用于控制目标函数中两项（“寻找 margin 最大的超平面” 和 “保证数据点偏差量最小”）之间的权重。注意，其中\xi是需要优化的变量（之一），而C是一个事先确定好的常量。完整地写出来是这个样子：

\begin{align} \min & \frac{1}{2}\|w\|^2 + C\sum_{i=1}^n\xi_i \\ s.t., & y_i(w^Tx_i+b) \geq 1-\xi_i, i=1,\ldots,n \\ & \xi_i \geq 0, i=1,\ldots,n \end{align}

用之前的方法将限制加入到目标函数中，得到如下问题：

\mathcal{L}(w,b,\xi,\alpha,r)=\frac{1}{2}\|w\|^2 + C\sum_{i=1}^n\xi_i – \sum_{i=1}^n\alpha_i \left(y_i(w^Tx_i+b)-1+\xi_i\right) – \sum_{i=1}^n r_i\xi_i

分析方法和前面一样，转换为另一个问题之后，我们先让\mathcal{L}针对w、b和\xi最小化：

\begin{align} \frac{\partial \mathcal{L}}{\partial w}=0 &\Rightarrow w=\sum_{i=1}^n \alpha_i y_i x_i \\ \frac{\partial \mathcal{L}}{\partial b} = 0 &\Rightarrow \sum_{i=1}^n \alpha_i y_i = 0 \\ \frac{\partial \mathcal{L}}{\partial \xi_i} = 0 &\Rightarrow C-\alpha_i-r_i=0, \quad i=1,\ldots,n \end{align}

将w带回\mathcal{L}并化简，得到和原来一样的目标函数：

\[ \max_\alpha \] \sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle x_i,x_j\rangle

不过，由于我们得到C-\alpha_i-r_i=0，而又有r_i \geq 0（作为 Lagrange multiplier 的条件），因此有\alpha_i \leq C，所以整个 dual 问题现在写作：

\begin{align} \[ \max_\alpha \] &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle x_i,x_j\rangle \\ s.t., &0 \leq \alpha_i\leq C, i=1,\ldots,n \\ &\sum_{i=1}^n\alpha_iy_i = 0 \end{align}

和之前的结果对比一下，可以看到唯一的区别就是现在 dual variable\alpha多了一个上限C。而 Kernel 化的非线性形式也是一样的，只要把 \langle x_i,x_j \rangle换成\kappa(x_i,x_j)即可。这样一来，一个完整的，可以处理线性和非线性并能容忍噪音和 outliers 的支持向量机才终于介绍完毕了。 😄

张驰原，网络 id pluskid，MIT 计算机博士在读，假装的 Julia 语言爱好者。