6

大角度非迭代的空间坐标旋转C#实现 - Aidan_Lee

 1 year ago
source link: https://www.cnblogs.com/AidanLee/p/16988300.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

大角度非迭代的空间坐标旋转C#实现

在前面文章中提到空间直角坐标系相互转换，测绘坐标转换时，一般涉及到的情况是：两个直角坐标系的小角度转换。这个就是我们经常在测绘数据处理中，WGS-84坐标系、54北京坐标系、80西安坐标系、国家2000坐标系之间的转换。

所谓小角度转换，指直角坐标系XOYXOY和直角坐标系X′O′Y′X′O′Y′之间，对应轴的旋转角度很小，满足泰勒级数展开后的线性模型。

1671185879422

常见的三维坐标转换模型有[1]：

  • 布尔沙模型
  • 莫洛琴斯基模型

但，当两个坐标系对应轴的旋转角度大道一定程度时，则无法使用低阶的泰勒级数展开，且迭代的计算量、精度、速度无法取得平衡[2]。存在以下缺点：

  1. 仅适用于满足近似处理的小角度转换
  2. 设计复杂的三角函数运算
  3. 需要迭代计算

罗德里格矩阵是摄影测量中的常见方法，在该方法中，不需要进行三角函数的计算和迭代运算。计算过程简单明了，易于编程实现。不仅适用于小角度的坐标转换，也适用于大角度的空间坐标转换。

本文将介绍罗德里格矩阵的基本原理和C#实现，并用实例证明解算的有效性。

2. 罗德里格矩阵坐标转换原理

2.1 坐标转换基本矩阵

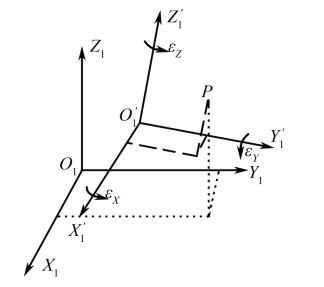
两个空间直角坐标系分别为XOYXOY和X′O′Y′X′O′Y′，坐标系原点不一致，存在三个平移参数ΔXΔX、ΔYΔY、ΔZΔZ。它们间的坐标轴也相互不平行，存在三个旋转参数ϵxϵx、ϵyϵy、ϵzϵz。同一点A在两个坐标系中的坐标分别为(X,Y,Z)(X,Y,Z)和(X′,Y′,Z′)(X′,Y′,Z′)。

显然，这两个坐标系通过坐标轴的平移和旋转变换可取得，坐标间的转换关系如下:

⎡⎣⎢XYZ⎤⎦⎥=λR⎡⎣⎢X′Y′Z′⎤⎦⎥+⎡⎣⎢ΔXΔYΔZ⎤⎦⎥(1)(1)[XYZ]=λR[X′Y′Z′]+[ΔXΔYΔZ]

其中，λλ是比例因子，R(εY)R(εX)R(εZ)R(εY)R(εX)R(εZ)分别是绕Y轴，X轴，Z轴的旋转矩阵。注意，旋转的顺序不同，RR 的表达形式不同。

R=R(εY)R(εX)R(εZ)=⎡⎣⎢cosεYcosεZ−sinεYsinεXsinεZcosεXsinεZsinεYcosεZ+cosεYsinεXsinεZ−cosεYsinεZ−sinεYsinεXcosεZcosεXcosεZ−sinεYsinεZ+cosεYsinεXcosεZ−sinεYcosεX−sinεXcosεYcosεX⎤⎦⎥R=R(εY)R(εX)R(εZ)=[cos⁡εYcos⁡εZ−sin⁡εYsin⁡εXsin⁡εZ−cos⁡εYsin⁡εZ−sin⁡εYsin⁡εXcos⁡εZ−sin⁡εYcos⁡εXcos⁡εXsin⁡εZcos⁡εXcos⁡εZ−sin⁡εXsin⁡εYcos⁡εZ+cos⁡εYsin⁡εXsin⁡εZ−sin⁡εYsin⁡εZ+cos⁡εYsin⁡εXcos⁡εZcos⁡εYcos⁡εX]

习惯上称RR为旋转矩阵，[ΔX,ΔY,ΔZ]T[ΔX,ΔY,ΔZ]T为平移矩阵。只要求出ΔXΔX、ΔYΔY 、ΔZΔZ，εXεX、εYεY、εZεZ，这7个转换参数,或者直接求出旋转矩阵和平移矩阵,就可以实现两个坐标系间的转换。

2.2 计算技巧-重心矩阵

为计算方便，对所用到的坐标进行重心化处理。将两个坐标系的公共点的坐标均化算为以重心为原点的重心化坐标。分别记为(X¯,Y¯,Z¯)(X¯,Y¯,Z¯) 和 (X¯′,Y¯′,Z¯′)(X¯′,Y¯′,Z¯′) 。两个坐标系的重心的坐标分别为 (Xg,Yg,Zg)(Xg,Yg,Zg) 和 (X′g,Y′g,Z′g)(Xg′,Yg′,Zg′) 。

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪Xk=∑ni=1Xin,Yk=∑ni=1Yin,Zk=∑ni=1ZinX′k=∑ni=1X′in,Y′k=∑ni=1Y′in,Z′k=∑ni=1Z′inX¯i=Xi−Xk,Y¯i=Yi−Yk,Z¯i=Zi−ZkX¯′i=X′i−X′k,Y¯′i=Y′i−Y′k,Z¯′i=Z′i−Z′k{Xk=∑i=1nXin,Yk=∑i=1nYin,Zk=∑i=1nZinXk′=∑i=1nXi′n,Yk′=∑i=1nYi′n,Zk′=∑i=1nZi′nX¯i=Xi−Xk,Y¯i=Yi−Yk,Z¯i=Zi−ZkX¯i′=Xi′−Xk′,Y¯i′=Yi′−Yk′,Z¯i′=Zi′−Zk′

因此，可以将式(1)变为：

⎡⎣⎢X¯Y¯Z¯⎤⎦⎥=λR⎡⎣⎢⎢X¯′Y¯′Z¯′⎤⎦⎥⎥(2)(2)[X¯Y¯Z¯]=λR[X¯′Y¯′Z¯′]
⎡⎣⎢ΔXΔYΔZ⎤⎦⎥=⎡⎣⎢XgYgZg⎤⎦⎥−λR⎡⎣⎢X′gY′gZ′g⎤⎦⎥(3)(3)[ΔXΔYΔZ]=[XgYgZg]−λR[Xg′Yg′Zg′]

因而，转换参数可分两步来求解。先用式(2)求出旋转参数和比例因子，再用式(,3)求出平移参数。

2.3 基于罗德里格斯矩阵的转换方法

对式(2)两边取2-范数，由于λ>0λ>0，旋转矩阵为正交阵的特性，可得:

∥[X¯,Y¯,Z¯]T∥=λ∥[X′¯,Y′¯,Z′¯]T∥(4)(4)‖[X¯,Y¯,Z¯]T‖=λ‖[X′¯,Y′¯,Z′¯]T‖

对于n个公共点，可得λλ的最小均方估计:

λ=∑ni=1(∥∥[X¯iY¯iZ¯i]T∥∥⋅∥∥∥[X¯′iY¯′iZ¯′i]T∥∥∥)∑ni(∥∥∥[X¯′′Y¯′iZ¯′i]T∥∥∥)2λ=∑i=1n(‖[X¯iY¯iZ¯i]T‖⋅‖[X¯i′Y¯i′Z¯i′]T‖)∑in(‖[X¯′′Y¯i′Z¯i′]T‖)2

得到比例因子的最小均方估计后，可将旋转矩阵 RR 表示为:

R=(I−S)−1(I+S)(5)(5)R=(I−S)−1(I+S)

其中，II为单位矩阵，SS为反对称矩阵。将式(5)带入式(3)，可得：

⎡⎣⎢⎢X¯−λX¯′Y¯−λY¯′Z¯−λZ¯′⎤⎦⎥⎥=⎡⎣⎢⎢⎢⎢0−(Z¯+λZ¯′)Y¯+λY¯′−(Z¯+λZ¯′)0X¯+λX¯′−(Y¯+λY¯′)X¯+λX¯′0⎤⎦⎥⎥⎥⎥⎡⎣⎢abc⎤⎦⎥(6)(6)[X¯−λX¯′Y¯−λY¯′Z¯−λZ¯′]=[0−(Z¯+λZ¯′)−(Y¯+λY¯′)−(Z¯+λZ¯′)0X¯+λX¯′Y¯+λY¯′X¯+λX¯′0][abc]

3. C#代码实现

矩阵运算使用MathNet.Numerics库，初始化字段MatrixBuilder<double> mb = Matrix<double>.Build和VectorBuilder<double> vb = Vector<double>.Build

3.1 计算矩阵重心坐标

Vector<double> BarycentricCoord(Matrix<double> coordinate){ Vector<double> barycentric = vb.Dense(3, 1); int lenCoord = coordinate.ColumnCount; if (lenCoord > 2) barycentric = coordinate.RowSums(); barycentric /= lenCoord; return barycentric;}

3.2 计算比例因子

取2-范数使用点乘函数PointwisePower(2.0)：

double ScaleFactor(Matrix<double> sourceCoord, Matrix<double> targetCoord){ double k = 0; double s1 = 0; double s2 = 0; Vector<double> sourceColL2Norm = sourceCoord.PointwisePower(2.0).ColumnSums(); Vector<double> targetColL2Norm = targetCoord.PointwisePower(2.0).ColumnSums(); int lenSourceCoord = sourceCoord.ColumnCount; int lenTargetCoord = targetCoord.ColumnCount; //只有在目标矩阵和源矩阵大小一致时，才能计算 if (lenSourceCoord == lenTargetCoord) { s1 = sourceColL2Norm.PointwiseSqrt().PointwiseMultiply(targetColL2Norm.PointwiseSqrt()).Sum(); s2 = sourceColL2Norm.Sum(); } k = s1 / s2; return k;}

3.3 计算罗德里格参数

这里的罗德里格参数就是式(6)中的[a,b,c]T[a,b,c]T。

Vector<double> RoderickParas(double scalceFactor, Matrix<double> sourceCoord, Matrix<double> targetCoord){ Vector<double> roderick = vb.Dense(new double[] { 0, 0, 0 }); int lenData = sourceCoord.ColumnCount; //常系数矩阵 var lConstant = vb.Dense(new double[3 * lenData]); //系数矩阵 var coefficient = mb.DenseOfArray(new double[3 * lenData, 3]); //构造相应矩阵 for (int i = 0; i < lenData; i++) { lConstant[3 * i] = targetCoord[0, i] - scalceFactor * sourceCoord[0, i]; lConstant[3 * i + 1] = targetCoord[1, i] - scalceFactor * sourceCoord[1, i]; lConstant[3 * i + 2] = targetCoord[2, i] - scalceFactor * sourceCoord[2, i]; coefficient[3 * i, 0] = 0; coefficient[3 * i, 1] = -(targetCoord[2, i] + scalceFactor * sourceCoord[2, i]); coefficient[3 * i, 2] = -(targetCoord[1, i] + scalceFactor * sourceCoord[1, i]); coefficient[3 * i + 1, 0] = -(targetCoord[2, i] + scalceFactor * sourceCoord[2, i]); coefficient[3 * i + 1, 1] = 0; coefficient[3 * i + 1, 2] = targetCoord[0, i] + scalceFactor * sourceCoord[0, i]; coefficient[3 * i + 2, 0] = targetCoord[1, i] + scalceFactor * sourceCoord[1, i]; coefficient[3 * i + 2, 1] = targetCoord[0, i] + scalceFactor * sourceCoord[0, i]; coefficient[3 * i + 2, 2] = 0; } roderick = coefficient.TransposeThisAndMultiply(coefficient).Inverse() * coefficient.Transpose() * lConstant; return roderick;}

3.4 解析罗德里格矩阵

此处，就是式(5)的实现。

/// <summary>/// 解析罗德里格矩阵为旋转矩阵和平移矩阵/// </summary>/// <param name="scaleFactor">比例因子</param>/// <param name="roderick">罗德里格矩阵</param>/// <param name="coreSourceCoord">原坐标系坐标</param>/// <param name="coreTargetCoord">目标坐标系坐标</param>/// <returns></returns>(Matrix<double>, Vector<double>) RotationMatrix(double scaleFactor, Vector<double> roderick, Vector<double> coreSourceCoord, Vector<double> coreTargetCoord){ Matrix<double> rotation = mb.DenseOfArray(new double[,] { {0,0,0 }, {0,0,0 }, {0,0,0 } }); //反对称矩阵 Matrix<double> antisymmetric = mb.DenseOfArray(new double[,] { { 0, -roderick[2], -roderick[1] }, {roderick[2], 0, -roderick[0] }, {roderick[1], roderick[0], 0 } }); // 创建单位矩阵 // 然后与式(5)的 S 执行 + 和 - 操作 rotation = (DenseMatrix.CreateIdentity(3) - antisymmetric).Inverse() * (DenseMatrix.CreateIdentity(3) + antisymmetric); translation = coreTargetCoord - scaleFactor * rotation * coreSourceCoord; return (rotation, translation);}

3.5 调用逻辑

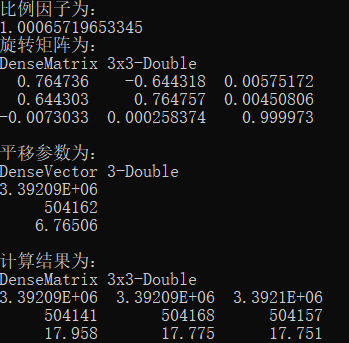
// 1. 字段值准备MatrixBuilder<double> mb = Matrix<double>.Build;VectorBuilder<double> vb = Vector<double>.Build; // 2. 写入源坐标系的坐标。注意这里的x,y,z输入顺序Matrix<double> source = mb.DenseOfArray(new double[,]{ {-17.968, -12.829, 11.058 }, {-0.019 , 7.117, 11.001 }, {0.019 , -7.117, 10.981 }}).Transpose(); // 3. 写入目标坐标系的坐标Matrix<double> target = mb.DenseOfArray(new double[,]{ { 3392088.646,504140.985,17.958 }, { 3392089.517,504167.820,17.775 }, { 3392098.729,504156.945,17.751 }}).Transpose(); // 4. 重心化var coreSource = BarycentricCoord(source);var coreTarget = BarycentricCoord(target); var sourceCoords = source - mb.DenseOfColumnVectors(coreSource, coreSource, coreSource);var targetCoords = target - mb.DenseOfColumnVectors(coreTarget, coreTarget, coreTarget); // 5. 求比例因子double k = ScaleFactor(sourceCoords, targetCoords); // 6. 解算咯德里格参数var roderick = RoderickParas(k, sourceCoords, targetCoords); // 7. 旋转(Matrix<double> ro, Vector<double> tran) = RotationMatrix(k, roderick, coreSource, coreTarget); Console.WriteLine("比例因子为：");Console.WriteLine(k); Console.WriteLine("旋转矩阵为：");Console.WriteLine(ro.ToString()); Console.WriteLine("平移参数为：");Console.WriteLine(tran.ToString()); Console.WriteLine("计算结果为：");Console.WriteLine(source2.ToString());

基于罗德里格矩阵的转换方法，在求解两个坐标系间的转换参数，特别是旋转角较大时，实现简单、快速。

1671195869776

  1. 朱华统,杨元喜,吕志平.GPS坐标系统的变换[M].北京:测绘出版社,1994. ↩︎

  2. 詹银虎,郑勇,骆亚波,等.无需初值及迭代的天文导航新算法0﹒测绘科学技术学报，2015,32(5):445-449. ↩︎


report

Recommend

About Joyk


Aggregate valuable and interesting links.
Joyk means Joy of geeK