【SVM】理论与实现

2017年09月28日

Author: Guofei

文章归类: 2-1-有监督学习，文章编号: 222

版权声明：本文作者是郭飞。转载随意，但需要标明原文链接，并通知本人
原文链接：https://www.guofei.site/2017/09/28/svm.html

Edit

本文涉及以下内容

SVM模型原理
confusion matrix的实现
用pickle保存和加载模型

简介

SVM的优势是可以解决小样本、非线性、高维模式识别的问题1

SVM建立在统计学习理论中的VC维理论和结构风险最小理论的基础上，根据有限样本信息在模型的复杂性（即对特定训练样本的学习精度）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折中
数据点是n维实空间的点，希望把这些点用一个n-1维的超平面分开。这类分类器叫做线性分类器
有很多分类器符合这种要求。但是我们还希望找到最佳分割平面，也就是使得两个类的数据点间隔最大的那个平面。

优缺点

小样本也可以
可以解决高维问题
可以解决非线性问题
鲁棒性：不需要微调
计算简单，理论完善：基于VC推广理论框架
与传统统计理论相比，统计学习理论基本不涉及概率测度的定义和大数定律
建立了有限样本学习问题的统一框架
避免了神经网络的网络结构选择、过学习、欠学习以及局部最小值问题

对缺失数据敏感
kernel 的选择

算法原理

1. 若干定义

feature vector: x∈X=Rn
target: y∈Y={+1,−1}

函数间隔给定数据集T和超平面(w,b),超平面(w,b)关于样本点(xi,yi)的函数间隔为:
ˆγi=yi(wxi+b)
超平面(w,b)关于数据集T的函数间隔为:
γ=mini=1,…,Nˆγi 几何间隔 γi=ˆγi∣∣w∣∣
γ=ˆγ∣∣w∣∣

2. 间隔最大化

svm1

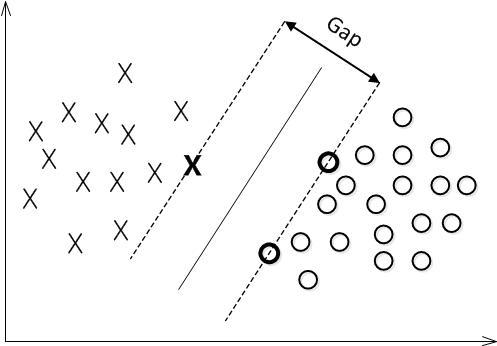
我们希望找到一条直线，使得 所有的间隔中最小的那些最大化
也就是：
maxw,bγ
s.t.yi(w∣∣w∣∣xi+b∣∣w∣∣)≥γ,i=1,2,…,N

等价于：
maxw,bˆγ∣∣w∣∣
s.t. yi(wxi+b)≥ˆγ,i=1,2,…,N

因为ˆγ和∣∣w∣∣可以等比例变化，所以取ˆγ=1，问题变成：
minw,b∣∣w∣∣2/2
s.t. yi(wxi+b)−1≥0,i=1,2,…N

可以证明，对于线性可分的样本集T, 最优解存在且唯一2。

3. 最优化求解

算法是 拉格朗日对偶法

Primal form(原问题)
minw,b∣∣w∣∣2/2
s.t. yi(w⋅xi+b)−1≥0,i=1,2,…,N

Dual from（对偶问题）
maxQ(α)=N∑i=1αi−0.5N∑i=1N∑j=1αiαjyiyj(xi⋅xj)
s.t. {N∑i=1αiyi=0αi≥0i=1,2,...,N

Decision function
f(x)=sgn(N∑i=1α∗yi(x⋅xi)+b∗)
w∗=N∑i=1α∗ixiyi
b∗=−0.5w∗⋅(xr+xs)

附：对偶问题的推导

原问题的拉格朗日函数是
L(w,b,α)=∣∣w∣∣2/2−N∑i=1αi[yi(wxi+b)−1]

问题转化为maxαminw,bL(w,b,α)

然后，求min那部分，用导数为0去算，然后带回去，就能得到对偶问题形式了。

trick

1. outlier

如果support vector 里存在 outlier 的话，其影响就很大3。
可能使超平面对于outlier非常敏感，甚至变成线性不可分问题。
为了处理这种情况，SVM 允许数据点在一定程度上偏离一下超平面。

对每个样本点(xi,yi)引入一个松弛变量ξi≥0,问题变成：
minw,b,ξ1/2∣∣w∣∣2+CN∑i=1ξi
s.t. {yi(w⋅xi+b)≥1−ξiξi≥0i=1,2,...,N

算法仍然是 拉格朗日对偶法
maxQ(α)=N∑i=1αi−0.5N∑i=1N∑j=1αiαjyiyj(xi⋅xj)
s.t. {N∑i=1αiyi=00≤αi≤Ci=1,2,...,N

2. hinge loss function

上面的优化问题等价于：
minw,bN∑i=1[1−yi(wxi+b)]++λ∣∣w∣∣2

其中，定义了合页损失函数(hinge loss function)：
[z]+={z,z>00,z≤0

从上面的推导可知，λ 越大，越倾向于把模型分开。λ越小，会有更多的跨越边界的点

3. 核函数

在解决非线性问题时，可以把数据映射到高维空间3, 并且用Kernel去做这个映射会比较方便。

核函数 X是输入空间，H是希尔伯特空间4,
存在映射ϕ(x):X→H，
使得∀x,z∈X, K(x,z)=ϕ(x)⋅ϕ(z)

在这种定义下，对偶问题变成：
maxQ(α)=N∑i=1αi−1/2N∑i=1N∑j=1αiαjyiyjK(xi,xj)
s.t. {N∑i=1αiyi=00≤αi≤C,i=1,2,...,N

Decision function
f(x)=sgn(w∗⋅Φ(x)+b∗)
=sgn(N∑i=1α∗yiΦ(xi)Φ(x)+b∗)
=sgn(N∑i=1α∗yiK(xi,x)+b∗)
w∗=l∑i=1α∗iyiΦ(xi)
b∗=yj−N∑i=1α∗yiK(xi,xj)

kernel有以下几种：

多项式核k(x1,x2)=(<x1,x2>+R)d
高斯核k(x1,x2)=exp(−||x1−x2||22σ2)
高斯核把原始空间映射到无穷维空间，
- σ很大时，高次特征衰减很快，近似相当于低维空间
- σ很小时，可以将任意数据线性可分，但会带来严重的过拟合问题
线性核k(x1,x2)=<x1,x2>，就是线性SVM，为了编程时形式上的统一

支持向量机与神经网络

（上文Kernel部分的 Decision Function抄录下来）
f(x)=sgn(w∗⋅Φ(x)+b∗)
=sgn(N∑i=1α∗yiΦ(xi)Φ(x)+b∗)
=sgn(N∑i=1α∗yiK(xi,x)+b∗)
w∗=l∑i=1α∗iyiΦ(xi)
b∗=yj−N∑i=1α∗yiK(xi,xj)

发现可以写成很像神经网络的形式

svm2

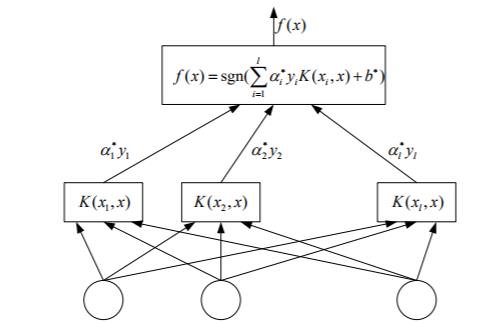
SVR

Vapnik等人在SVM分类的基础上引入了 不敏感损失函数 ，从而得到了回归型支持向量机（Support Vector Machine for Regression，SVR）。
SVM应用于回归拟合分析时，其基本思想不再是寻找一个最优分类面使得两类样本分开，而是寻找一个最优分类面使得 所有训练样本离该最优分类面的误差最小。

primal form
min0.5∣∣w∣∣2+CN∑i=1(ξi+ξ∗i)
s.t.{yi−w⋅Φ(xi)−b≤ε+ξi−yi+w⋅Φ(xi)+b≤ε+ξ∗iξi≥0ξ∗i≥0,i=1,2,...N

Dual form
maxα,α∗−0.5N∑i=1N∑i=1(αi−α∗i)(αj−α∗j)K(xi,xj)−N∑i=1(alphai+α∗i)ε+N∑i=1(αi−α∗i)yi
s.t.{N∑i=1(αi−α∗i)=00≤αi≤C0≤α∗i≤C,i=1,2,...N

Decision function
f(x)=N∑i=1(αi−α∗i)K(xi,x)+b∗
w∗=N∑i=1(αi−α∗i)Φ(xi)
b=…

Python示例

from sklearn import datasets
dataset=datasets.load_iris()

from sklearn import svm
clf=svm.SVC()
clf.fit(dataset.data,dataset.target)

clf.predict(dataset.data)#判断数据属于哪个类别
clf.score(dataset.data,dataset.target)#准确率
model.support_vectors_# get support vectors
model.support_# get indices of support vectors
model.n_support_# get number of support vectors for each class

model.decision_function_shape='ovo'
dec = model.decision_function([[0.6,1]])
#如果有n个类，那么上面的dec有n(n-1)/2列  

model.decision_function_shape='ovr'
dec = model.decision_function([[0.6,1]])
#dec有n列

Python 实现2

1. 生成数据

随机地生成数据5

import numpy as np
import pandas as pd
from scipy.stats import uniform
x1 = uniform.rvs(loc=0, scale=1, size=100)
x2 = uniform.rvs(loc=0, scale=2, size=100)
data = pd.DataFrame({'x1': x1, 'x2': x2})
data['y'] = (data['x1'] + 0.5 * data['x2'] < 1) * 1

2. 数据可视化

import matplotlib.pyplot as plt
plt.plot(data[data.y == 1]['x1'], data[data.y == 1]['x2'], '.')
plt.plot(data[data.y == 0]['x1'], data[data.y == 0]['x2'], '.')
plt.show()

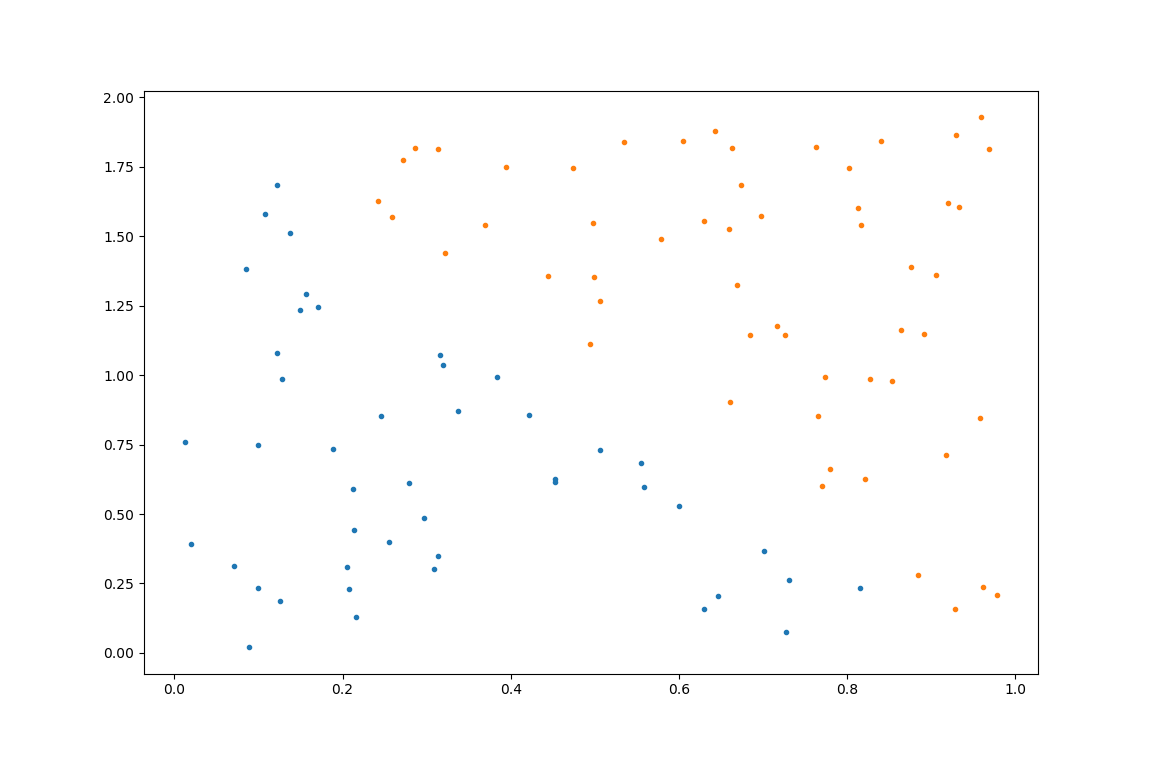
3. 选取训练集和测试集

from numpy.random import shuffle  # 引入随机函数
n=data.shape[0]
mac=np.arange(n)#掩码，用于随机打乱顺序
shuffle(mac)  # 随机打乱数据
data=data.loc[mac]
data_train = data.iloc[:int(0.8*n),:]  # 选取80%为训练数据
data_test = data.iloc[int(0.8*n):,:]  # 选取20%为测试数据

x_train = data_train.loc[:,['x1','x2']]
y_train = data_train.loc[:, 'y']#svm的y需要输入1darray
x_test = data_test.loc[:,['x1','x2']]
y_test = data_test.loc[:, ['y']]

这段代码不算太美丽，以后看看能不能改进

4. 模型计算

from sklearn import svm
model = svm.SVC()
model.fit(x_train, y_train)

5. 混淆矩阵

from sklearn import metrics

cm_train = metrics.confusion_matrix(y_train, model.predict(x_train))  # 训练样本的混淆矩阵
cm_test = metrics.confusion_matrix(y_test, model.predict(x_test))  # 测试样本的混淆矩阵
print(cm_train)
print(cm_test)

6. 模型保存

import pickle
pickle.dump(model, open('svm.model', 'wb'))
# 以后可以通过下面语句重新加载模型：
# model = pickle.load(open('../tmp/svm.model', 'rb'))

下次加载后，也不需要sklearn这个包了

一个多分类的案例

1. 随机生成数据并画图

import numpy as np
import pandas as pd
from scipy.stats import uniform
import matplotlib.pyplot as plt

x1 = uniform.rvs(loc=0, scale=1, size=1000)
x2 = uniform.rvs(loc=0, scale=2, size=1000)
data = pd.DataFrame({'x1': x1, 'x2': x2})
data['y'] = 0
data.loc[data['x1'] + 0.5 * data['x2'] > 0.7, 'y'] = 1
data.loc[data['x1'] + 0.5 * data['x2'] > 1.3, 'y'] = 2
plt.plot(data[data.y == 0]['x1'], data[data.y == 0]['x2'], '.')
plt.plot(data[data.y == 1]['x1'], data[data.y == 1]['x2'], '.')
plt.plot(data[data.y == 2]['x1'], data[data.y == 2]['x2'], '.')
plt.show()
print(data['y'].value_counts())

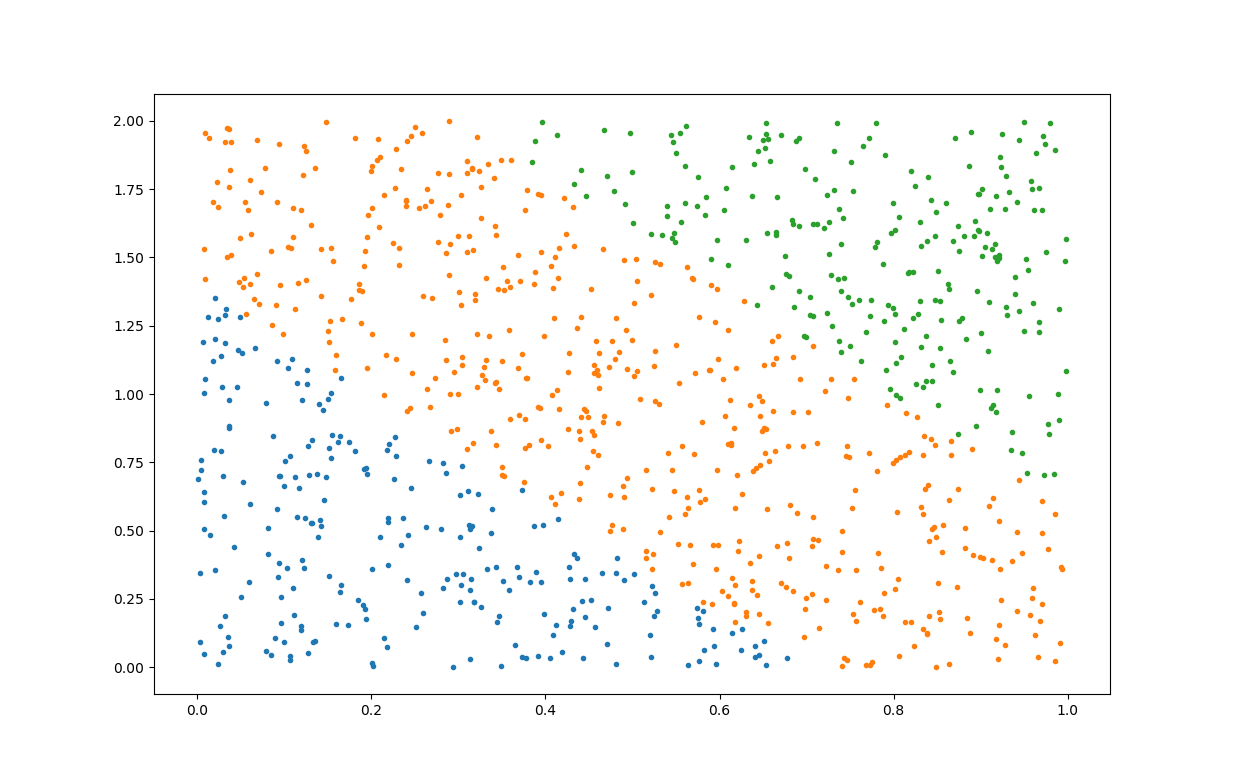
还有print的内容：

显示这个的原因是，有可能有某个类数量很少，导致test或train中没有这个类。
解决方法：

从业务或数据角度去解决。
每个类分别取test和train

2. 画图

3. 选取训练集和测试集

这里想保证每个类都有80%数据选入train，代码这样改：

from numpy.random import shuffle  # 引入随机函数
n=data.shape[0]
mac=np.arange(n)#掩码，用于随机打乱顺序
shuffle(mac)  # 随机打乱数据
data=data.loc[mac]

data_train=pd.DataFrame()
data_test=pd.DataFrame()
for i , t in data.groupby(data.loc[:,'y']):
    n_temp=t.shape[0]
    data_train=pd.concat([data_train,t.iloc[:int(0.8*n_temp)]])
    data_test=pd.concat([data_test,t.iloc[int(0.8*n_temp):]])

这里用了几个技巧，你可以想想自己能不能写出来

4. 模型计算

from sklearn import svm
model = svm.SVC()
model.fit(data_train.loc[:,['x1','x2']], data_train.loc[:,'y'])

5. 混淆矩阵

from sklearn import metrics

cm_train = metrics.confusion_matrix(data_train.loc[:,'y'], model.predict(data_train.loc[:,['x1','x2']]))  # 训练样本的混淆矩阵
cm_test = metrics.confusion_matrix(data_test.loc[:,'y'], model.predict(data_test.loc[:,['x1','x2']]))  # 测试样本的混淆矩阵
print(cm_train)
print(cm_test)

6. 模型保存

7. 模型应用

model.predict(data_test.loc[:,['x1','x2']])#预测

model.support_vectors_# get support vectors
model.support_# get indices of support vectors
model.n_support_# get number of support vectors for each class

model.decision_function_shape='ovo'
dec = model.decision_function([[0.6,1]])

如果有n个类，那么上面的dec有n(n-1)/2列

model.decision_function_shape='ovr'
dec = model.decision_function([[0.6,1]])

dec有n列

SVR

生成模拟数据

import sklearn.svm as svm
import numpy as np
from scipy import stats
rv=stats.uniform(loc=0,scale=9)
n_samples=1000
X=rv.rvs(size=(n_samples,1))
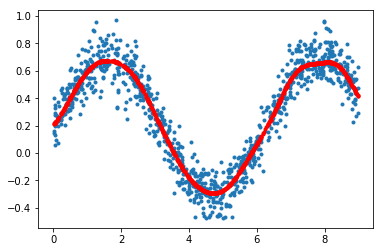
Y=0.5*np.sin(X[:,0])+0.2+stats.norm(loc=0,scale=0.1).rvs(size=n_samples)

model=svm.SVR(epsilon=0)#如果不确定epsilon大小，就设置为0
model.fit(X,Y)
y_hat=model.predict(X)

import matplotlib.pyplot as plt
plt.plot(X,Y,'.')
plt.plot(X,y_hat,'.r')
plt.show()

参考文献

您的支持将鼓励我继续创作！

【SVM】理论与实现

【SVM】理论与实现

Recommend

About Joyk