Implementing Dynamic Programming, ILP, Simulated Annealing and Genetic algorithms for TSP, 2-OPT Approximation Algorithm for Metric TSP and Polynomial-time DP algorithm for Bitonic TSP with python

In this blog we shall discuss on the Travelling Salesman Problem (TSP) — a very famous NP-hard problem and will take a few attempts to solve it (either by considering special cases such as Bitonic TSP and solving it efficiently or by using algorithms to improve runtime, e.g., using Dynamic programming, or by using approximation algorithms, e.g., for Metric TSP and heuristics, to obtain not necessarily optimal but good enough solutions, e.g., with Simulated Annealing and Genetic Algorithms) and work on the corresponding python implementations. Few of the problems discussed here appeared as programming assignments in the Coursera course Advanced Algorithms and Complexity and some of the problem statements are taken from the course.

Improving the runtime of the Travelling Salesman Problem with Dynamic Programming

In this problem we shall deal with a classical NP-complete problem called Traveling Salesman Problem. Given a graph with weighted edges, you need to find the shortest cycle visiting each vertex exactly once. Vertices correspond to cities. Edges weights correspond to the cost (e.g., time) to get from one vertex to another one. Some vertices may not be connected by an edge in the general case.

• Here we shall use dynamic programming to solve TSP: instead of solving one problem we will solve a collection of (overlapping) subproblems.
• A subproblem refers to a partial solution
• A reasonable partial solution in case of TSP is the initial part of a cycle
• To continue building a cycle, we need to know the last vertex as well as the set of already visited vertices
• It will be convenient to assume that vertices are integers from 1 to n and that the salesman starts his trip in (and also returns back to) vertex 1.
• The following figure shows the Dynamic programming subproblems, the recurrence relation and the algorithm for TSP with DP.

Implementation tips

• In order to iterate through all subsets of {1, . . . , n}, it will be helpful to notice that there is a natural one-to-one correspondence between integers in the range from 0 and 2^n − 1 and subsets of {0, . . . , n − 1}: k ↔ {i : i -th bit of k is 1}.
• For example, k = 1 (binary 001) corresponds to the set {0}, where k = 5 (binary 101) corresponds to the set {0,2}
• In order to find out the integer corresponding to S − {j} (for j ∈ S), we need to flip the j-th bit of k (from 1 to 0). For this, in turn, we can compute a bitwise XOR of k and 2^j (that has 1 only in j-th position)
• In order to compute the optimal path along with the cost, we need to maintain back-pointers to store the path.

The following python code shows an implementation of the above algorithm.

import numpy as np
from itertools import combinationsdef TSP(G):
   n = len(G)
   C = [[np.inf for _ in range(n)] for __ in range(1 << n)]
   C[1][0] = 0 # {0} <-> 1
   for size in range(1, n):
      for S in combinations(range(1, n), size):
	  S = (0,) + S
	  k = sum([1 << i for i in S])
	  for i in S:
	      if i == 0: continue
	      for j in S:
		 if j == i: continue
		    cur_index = k ^ (1 << i)
		    C[k][i] = min(C[k][i], C[cur_index][j]+ G[j][i])     
		                                       #C[S−{i}][j]
   all_index = (1 << n) - 1
   return min([(C[all_index][i] + G[0][i], i) \
                            for i in range(n)])

• The following animation shows how the least cost solution cycle is computed with the DP for a graph with 4 vertices. Notice that in order to represent C(S,i) from the algorithm, the vertices that belong to the set S are colored with red circles, the vertex i where the path that traverses through all the nodes in S ends at is marked with a red double-circle.
• The next animation also shows how the DP table gets updated. The DP table for a graph with 4 nodes will be of size 2⁴ X 4, since there are 2⁴=16 subsets of the vertex set V={0,1,2,3} and a path going through a subset of the vertices in V may end in any of the 4 vertex.
• The transposed DP table is shown in the next animation, here the columns correspond to the subset of the vertices and rows correspond to the vertex the TSP ends at.

Image by Author

• The following animation shows how the least cost solution cycle is computed with the DP for a graph with 5 nodes.

Image by Author

The following animation / figure shows the TSP optimal path is computed for increasing number of nodes (where the weights for the input graphs are randomly generated) and the exponential increase in the time taken.

Image by AuthorImage by Author

Solving TSP with Integer Linear Program

Solving with the mip package using the following python code, produces the output shown by the following animation, for a graph with randomly generated edge-weights.

from mip import Model, xsum, minimize, BINARY

def TSP_ILP(G):

start = time()
   V1 =  range(len(G))
   n, V = len(G), set(V1)
   model = Model()   # binary variables indicating if arc (i,j) is used 
   # on the route or not
   x = [[model.add_var(var_type=BINARY) for j in V] for i in V]   # continuous variable to prevent subtours: each city will have a
   # different sequential id in the planned route except the 1st one
   y = [model.add_var() for i in V]   # objective function: minimize the distance
    model.objective = minimize(xsum(G[i][j]*x[i][j] \
                               for i in V for j in V))

# constraint : leave each city only once
   for i in V:
      model += xsum(x[i][j] for j in V - {i}) == 1   # constraint : enter each city only once
   for i in V:
      model += xsum(x[j][i] for j in V - {i}) == 1   # subtour elimination
   for (i, j) in product(V - {0}, V - {0}):
      if i != j:
         model += y[i] - (n+1)*x[i][j] >= y[j]-n   # optimizing
   model.optimize()   # checking if a solution was found
   if model.num_solutions:
      print('Total distance {}'.format(model.objective_value))
      nc = 0 # cycle starts from vertex 0
      cycle = [nc]
      while True:
         nc = [i for i in V if x[nc][i].x >= 0.99][0]
	 cycle.append(nc)
	 if nc == 0:
	    break

return (model.objective_value, cycle)

The constraint to prevent the subtours to appear in the solution is necessary, if we run without the constraint, we get a solution with subtours instead of a single cycle going through all the nodes, as shown below:

Image by AuthorImage by Author

Comparing with Dynamic programming based solution, we can see that ILP is much more efficient for higher n values.

Image by AuthorImage by Author

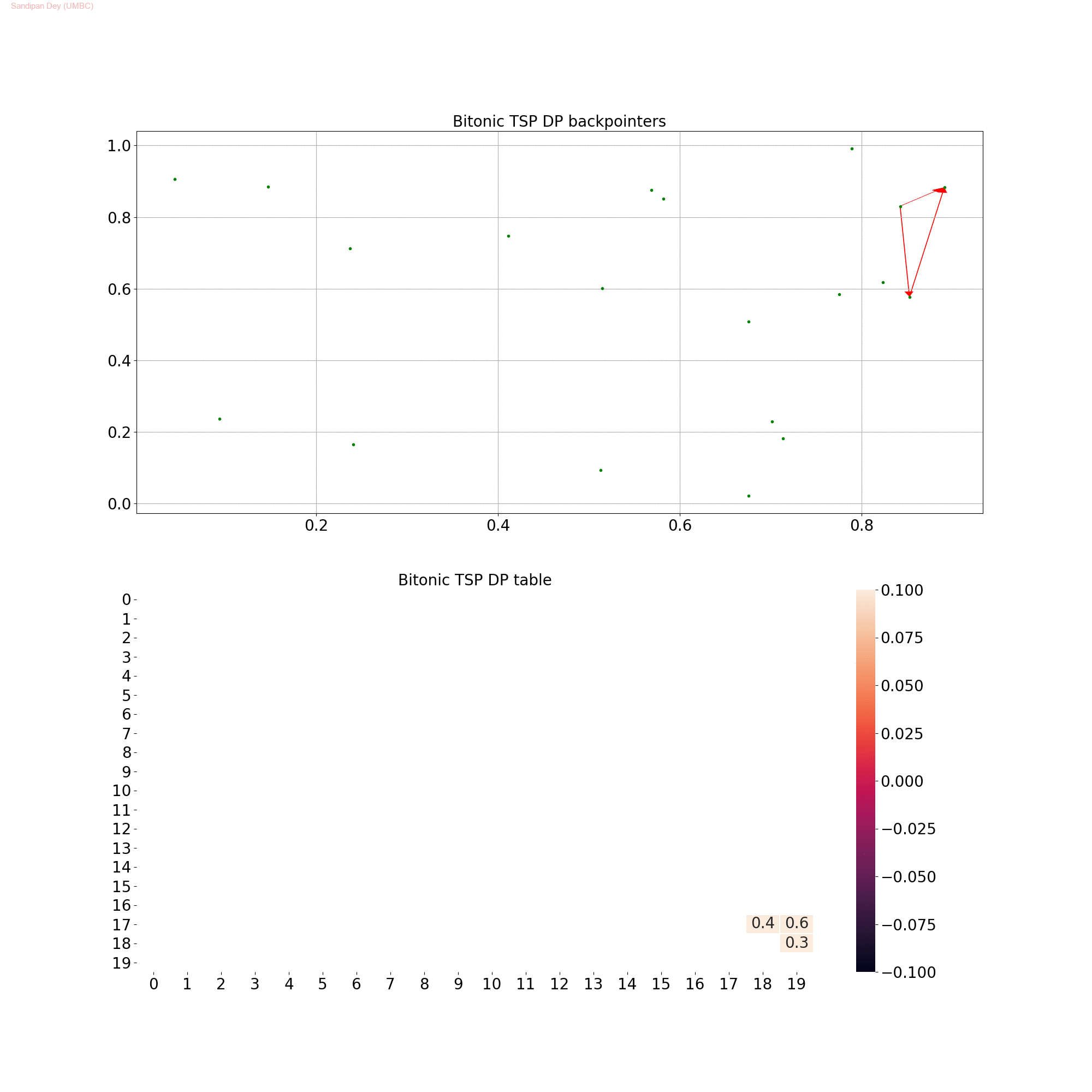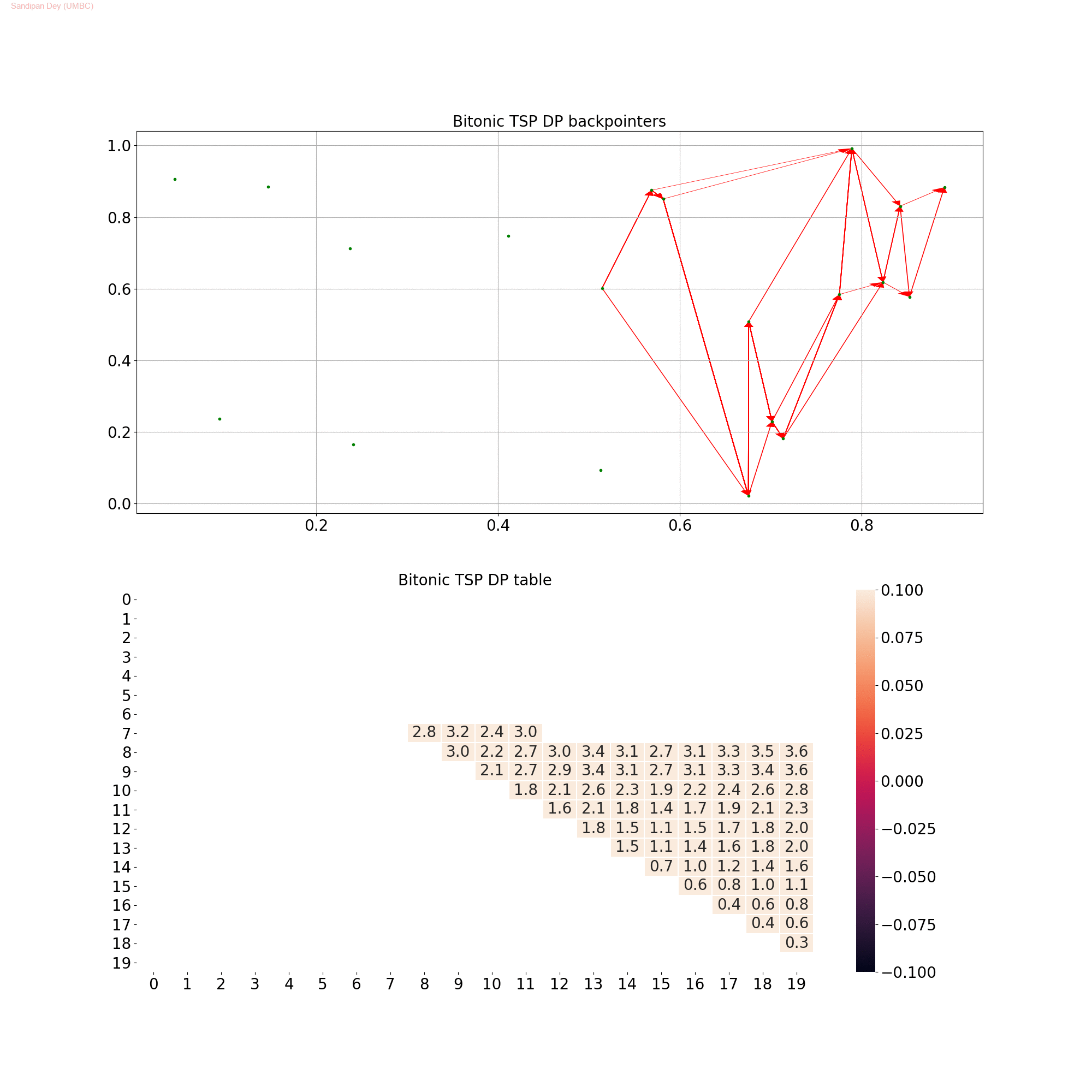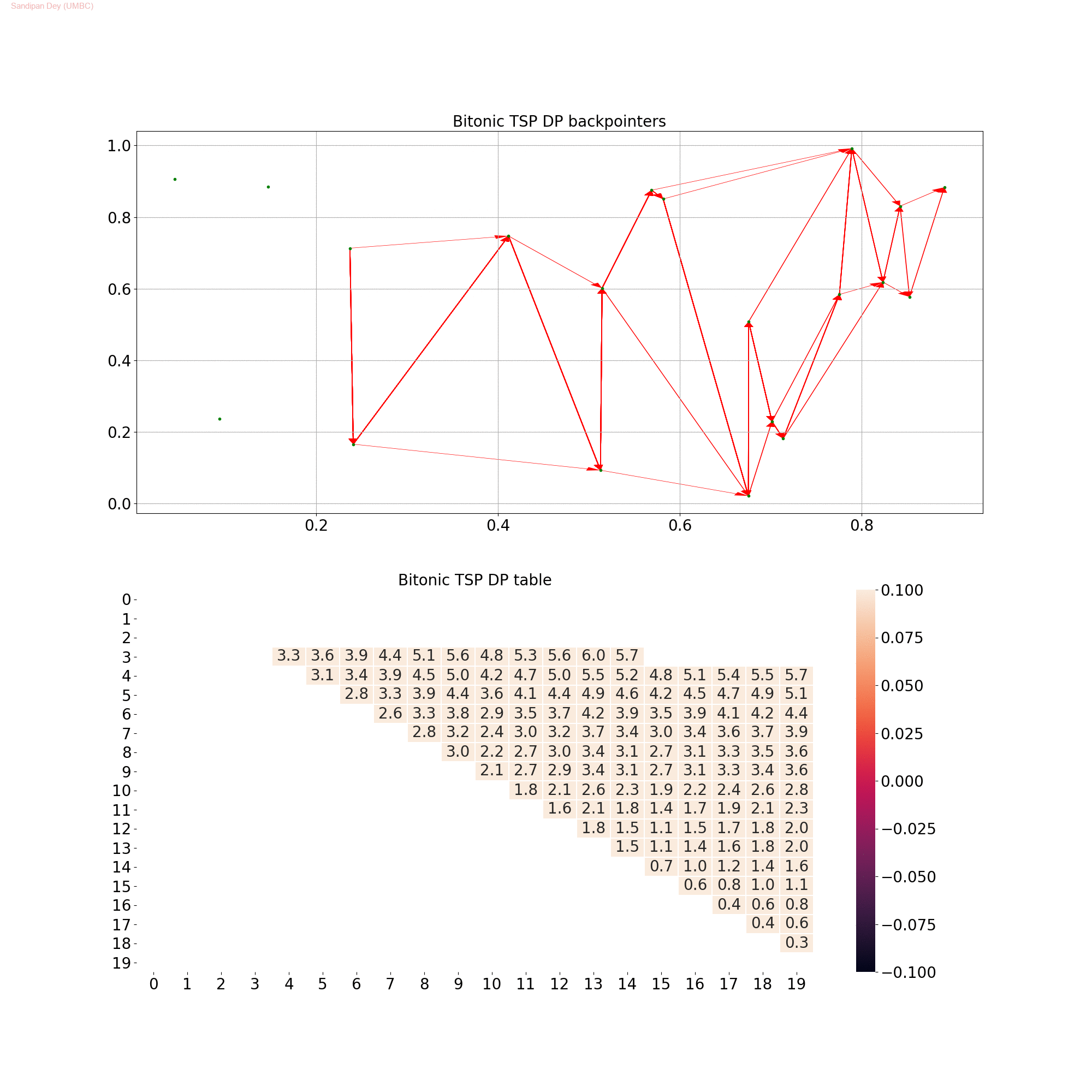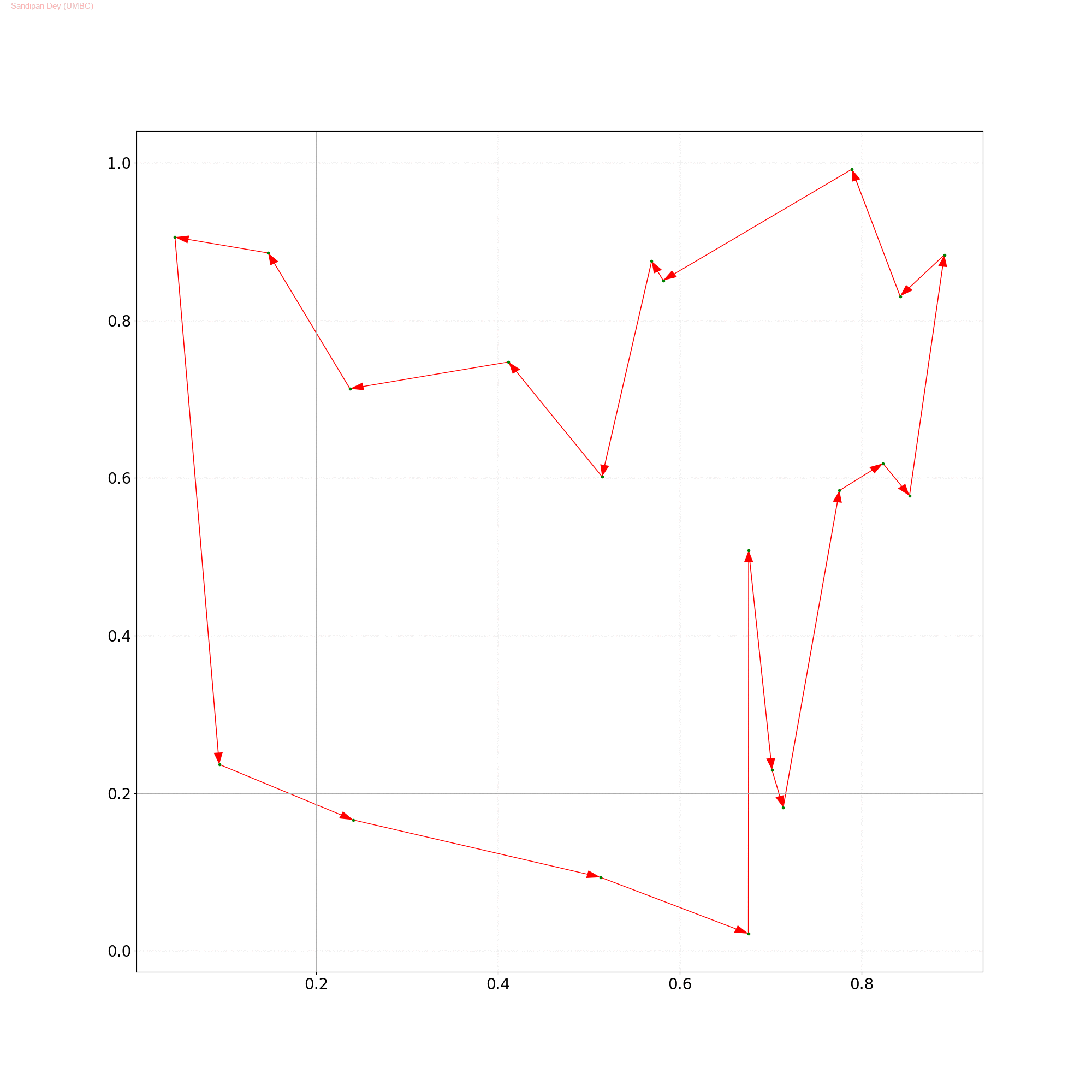
Bitonic TSP

Image by AuthorImage by Author

The following python code snippet implements the above DP algorithm.

def dist(P, i, j):
   return np.sqrt((P[i][0]-P[j][0])**2+(P[i][1]-P[j][1])**2)

def BTSP(P):
   n = len(P)
   D = np.ones((n,n))*np.inf
   path = np.ones((n,n), dtype=int)*(-1)
   D[n-2,n-1] = dist(P, n-2, n-1)
   path[n-2,n-1] = n-1
   for i in range(n-3,-1,-1):
      m = np.inf
      for k in range(i+2,n):
	 if m > D[i+1,k] + dist(P,i,k):
	    m, mk = D[i+1,k] + dist(P,i,k), k
      D[i,i+1] = m
      path[i,i+1] = mk
      for j in range(i+2,n):
	 D[i,j] = D[i+1,j] + dist(P,i,i+1)
	 path[i,j] = i+1	
      D[0,0] = D[0,1] + dist(P,0,1)
      path[0,0] = 1
      return D, path

def get_tsp_path(path, i, j, n):
    if n < 0:
	return []
    if i <= j:
 	k = path[i,j]
	return [k] + get_tsp_path(path, k, j, n-1)
    else:
	k = path[j,i]
	return get_tsp_path(path, i, k, n-1) + [k]

The following animation shows how the DP table is computed and the optimal path for Bitonic TSP is constructed. It also shows the final optimal path.

Image by AuthorImage by Author

2-OPT Approximation Algorithm for Metric TSP

The next code snippet implements the above 2-OPT approximation algorithm.

import numpy as np
import queue	def dfs(adj, x):
   visited = [False]*len(adj)
   stack = [x]
   visited[x] = True
   path = []
   while len(stack) > 0:
      u = stack.pop(-1)
      path.append(u)
      for v in adj[u]:
	 if not visited[v]:
	    stack.append(v)	
   	    visited[v] = True
	return pathdef mst(adj):
   inf = np.inf
   c = [inf]*n
   s = 0
   c[s] = 0
   visited = [False]*n
   parent = [None]*n
   h = queue.PriorityQueue()
   for v in range(n):
      h.put((c[v], v))
   edges = []
   while not h.empty():
      w, u = h.get()
      if visited[u]: continue
           visited[u] = True
	   if parent[u] != None:
		edges.append((parent[u], u))
		for v in range(n):
    		   if v == u: continue
		   if (not visited[v]) and (c[v] > adj[u][v]):
			c[v] = adj[u][v]
			parent[v] = u
			h.put((c[v], v))
   adj = [[] for _ in range(n)]
   for i in range(n):
      if parent[i] != None:
           adj[parent[i]].append(i)
   path = dfs(adj, 0)
   path += [path[0]]
   return path

The following animation shows the TSP path computed with the above approximation algorithm and compares with the OPT path computed using ILP for 20 points on 2D plane. The MST is computed with Prim’s algorithm.

Image by Author

TSP with Simulated Annealing

The following python code snippet shows how to implement the Simulated Annealing to solve TSP, here G represents the adjacency matrix of the input graph.

def TSP_SA(G):
   s = list(range(len(G)))
   c = cost(G, s)
   ntrial = 1
   T = 30
   alpha = 0.99
   while ntrial <= 1000:
      n = np.random.randint(0, len(G))
      while True:
         m = np.random.randint(0, len(G))
         if n != m:
            break
      s1 = swap(s, m, n)
      c1 = cost(G, s1)
      if c1 < c:
         s, c = s1, c1
      else:
         if np.random.rand() < np.exp(-(c1 - c)/T):
            s, c = s1, c1
      T = alpha*T
      ntrial += 1def swap(s, m, n):
   i, j = min(m, n), max(m, n)
   s1 = s.copy()
   while i < j:
      s1[i], s1[j] = s1[j], s1[i]
      i += 1
      j -= 1
   return s1

def cost(G, s):
   l = 0
   for i in range(len(s)-1):
      l += G[s[i]][s[i+1]]
   l += G[s[len(s)-1]][s[0]] 
   return l

The following animations show how the algorithm works:

Image by AuthorImage by Author

The following animation shows the TSP path computed with SA for 100 points in 2D.

Image by Author

TSP with Genetic Algorithm

Here in the following implementation of the above algorithm we shall have the following assumptions:

• We shall assume the crossover rate is 1.0, i.e., all individuals in a population participate in crossover. The mutation probability to be used is 0.1.
• With each crossover operation between two parent chromosomes, couple of children are generated, cant just swap portions of parents chromosomes, need to be careful to make sure that the offspring represents valid TSP path.
• Mutation is similar to swap operation implemented earlier.
• For each generation we shall keep a constant k=20 (or 30) chromosomes (representing candidate solutions for TSP).
• The fitness function will be the cost of the TSP path represented by each chromosome. Hence, we want to minimize the value of the fitness function — i.e., less the value of a chromosome, more fit is it to survive.
• We shall use rank selection, i.e., after crossover and mutation, only the top k fittest offspring (i.e., with least fitness function value) will survive for the next generation.
• The following python code shows the implementation of the above algorithm with the above assumptions.

import numpy as npdef do_crossover(s1, s2, m):
   s1, s2 = s1.copy(), s2.copy()
   c1 = s2.copy()
   for i in range(m, len(s1)): c1.remove(s1[i])
   for i in range(m, len(s1)): c1.append(s1[i])
   c2 = s1.copy()
   for i in range(m, len(s2)): c2.remove(s2[i])
   for i in range(m, len(s2)): c2.append(s2[i])	
   return (c1, c2)

def do_mutation(s, m, n):
   i, j = min(m, n), max(m, n)
   s1 = s.copy()
   while i < j:
	s1[i], s1[j] = s1[j], s1[i]
	i += 1
	j -= 1
   return s1

def compute_fitness(G, s):
   l = 0
   for i in range(len(s)-1):
	l += G[s[i]][s[i+1]]
	l += G[s[len(s)-1]][s[0]]	
   return l

def get_elite(G, gen, k):
   gen = sorted(gen, key=lambda s: compute_fitness(G, s))
   return gen[:k]

def TSP_GA(G, k=20, ntrial = 200):
    n_p = k
    mutation_prob = 0.1
    gen = []
    path = list(range(len(G)))
    while len(gen) < n_p:
  	path1 = path.copy()
	np.random.shuffle(path1)
	if not path1 in gen:
		gen.append(path1)

for trial in range(ntrial):
	gen = get_elite(G, gen, k)
	gen_costs = [(round(compute_fitness(G, s),3), s) \
                      for s in gen]
	next_gen = []
	for i in range(len(gen)):
   	   for j in range(i+1, len(gen)):
   	       c1, c2 = do_crossover(gen[i], gen[j], \
		        np.random.randint(0, len(gen[i])))
	       next_gen.append(c1)
	       next_gen.append(c2)
	   if np.random.rand() < mutation_prob:
	       m = np.random.randint(0, len(gen[i]))
	       while True:
	          n = np.random.randint(0, len(gen[i]))
		  if m != n:
		     break
	       c = do_mutation(gen[i], m, n)
	       next_gen.append(c)
	gen = next_gen

Image by Author

The following animation shows the TSP path computed with GA for 100 points in 2D.

Image by Author