

快速傅里叶变换FFT学习笔记 - DengDuck
source link: https://www.cnblogs.com/dengduck/p/FFT.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

点值表示法
我们正常表示一个多项式的方式,形如 A(x)=a0+a1x+a2x2+...+anxnA(x)=a0+a1x+a2x2+...+anxn,这是正常人容易看懂的,但是,我们还有一种表示法。
我们知道,n+1n+1个点可以表示出一个 nn 次的多项式。
于是,我们任意地取 n+1n+1 个不同的值,表示 xx ,求出的值与 xx 对应,形成 n+1n+1个点,这就可以表示。
一种表示坐标的方法,对于坐标 (x,y)(x,y),可写作 x+iyx+iy,其中xx为实部,yy为虚部。
C++中有复数的模板,complex,可以直接作为变量类型使用。
运算规则,自然不用多说了,也就是直接拿式子算即可。
如果你不会,可以看看百度百科。
我们将点至原点的距离称为模长,将其与原点相连之后与 xx 轴形成的一个夹角称为辐角,不过呢,对于第三第四象限的点,自然要加上一个 180°180°了。
我的表述自然不够专业,希望可以表述出这个意思吧。
复数的乘法可以理解为,模长相乘,辐角相加。
Tips:
此部分的证明来自 cjx 犇犇。
为啥是这样呢?证明如下:
那么这个点就是 (ac−bd,bc+ad)(ac−bd,bc+ad),其模长:
那么我们应该可以看出来这个模长相乘了。
接下来是辐角相加,我们设原来两个辐角为 θ1,θ2θ1,θ2,而模长为 t1,t2t1,t2。
我们知道分母是乘积的模长,分子是横坐标,所以这个式子恰好就是乘积辐角对应的 coscos 值。
那么显然,辐角的值就是 θ1+θ2θ1+θ2了。
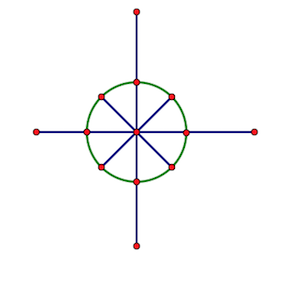
如图是坐标轴上一个以原点为圆心的半径为 11 的圆。
我们定义ωknωnk表示从(1,0)(1,0)开始,把圆均分为nn份的第kk个点的复数,其中(1,0)(1,0)为ω0nωn0。
那么,不难发现,ωknωnk表示的点为 (cos(2πkn),sin(2πnk))(cos(2πkn),sin(2πnk))。
这是为什么呢?我们考虑它的辐角,由于其平分了一整个圆,所以其辐角为 360kn°360kn°,转换为弧度后则为 2πkn2πkn,且模长为 11,利用三角函数易得其坐标了。
简单推推式子不难发现 (ω1n)k=ωkn(ωn1)k=ωnk,这是利用了模长相乘,辐角相加,因为模长是 11 ,怎么乘都是 11,于是辐角不断叠加,从定义上看是这样的。
- 性质1:ωdkdn=ωknωdndk=ωnk,根据定义可证。
- 性质2:ωk+n2n=−ωknωnk+n2=−ωnk,两点对称。
这个东西有什么用呢?
离散傅里叶变换
离散傅里叶变换(Discrete Fourier Transform,简称DFT)的思想是利用 ωknωnk将一个多项式转为点值表示法。
对于一个多项式A(x)=a0+a1x+a2x2+...+an−1xn−1A(x)=a0+a1x+a2x2+...+an−1xn−1,我们按照前文所云,将所有的 ωknωnk作为 xx 代入。
于是我们得到了 n−1n−1 个点,使用复数形式表示,成为一个数组 (y0,y1,y2,...,yn−1)(y0,y1,y2,...,yn−1)的。
这被称为 A(x)A(x) 的傅里叶变换。
傅里叶逆变换
我们再将其作为一个多项式 B(x)=y0+y1x+....+yn−1xn−1B(x)=y0+y1x+....+yn−1xn−1。
对于这个多项式B(x)B(x),代入所有的 ω−knωn−k,也就是ωknωnk的倒数,得到 (z0,z1,z2,...,zn−1)(z0,z1,z2,...,zn−1)。
关于后面那个等比数列,若 j=kj=k,可得 11,否则用等比数列式子可知为 00。
所以我们可以求出原来的多项式了。
快速傅里叶变换
快速傅里叶变换(Fast Fourier Transform,简称FFT),是在 DFT的基础上我们发现时间复杂度依然需要 O(n2)O(n2),没有含金量,所以我们要给他含金量!
我们可以使用分治的思想,使得时间复杂度降至O(nlogn)O(nlogn)。
对于A(x)=a0+a1x+a2x2+...+an−1xn−1A(x)=a0+a1x+a2x2+...+an−1xn−1,我们可以:
不错!利用这两个式子,我们可以在 O(nlogn)O(nlogn) 的时间复杂度求出 A(x)A(x)。
不过注意这里一直有一个除二操作,为了方便,我们需要把多项式补成一个次数为2x−12x−1 的多项式。
可以写一个递归来求解。
注意这个取倒可以利用共轭复数,对于 a+iba+ib,其共轭复数为 a−iba−ib。
由于此处 a2+b2=1a2+b2=1 ,因此其共轭复数为其倒数。
void FFT(cp *a,LL n,bool inv)//inv 表示omega是否取倒{ if(n==1)return; static cp buf[N]; LL m=n/2; for(int i=0;i<=m-1;i++)buf[i]=a[2*i],buf[i+m]=a[2*i+1];//奇偶分开 for(int i=0;i<=n-1;i++)a[i]=buf[i]; FFT(a,m,inv),FFT(a+m,m,inv); for(int i=0;i<=m-1;i++) { cp x=omega(n,i); if(inv)x=conj(x);//conj(x)求解共轭复数 buf[i]=a[i]+x*a[i+m],buf[i+m]=a[i]-x*a[i+m]; } for(int i=0;i<=n-1;i++)a[i]=buf[i];}
利用FFT求解多项式的乘积
这个还是十分简单的,直接把两个多项式转化为两个长度相同的次数为2x−12x−1的多项式。
求解出其傅里叶变换形式之后,对于每个点对应的复数,相乘即可。
为什么呢?
首先我们知道当前的 aiai表示的是 A(ωin)A(ωni),bibi表示的是 B(ωin)B(ωni),那么我们将两个值直接相乘。
因此多项式相乘以后,我们希望 ai=A(ωin)B(ωin)ai=A(ωni)B(ωni),那么就是直接相乘喽。
给一个简单的实现:
、#include<bits/stdc++.h>#define LL int#define cp complex<double>using namespace std;const double PI=acos(-1.0000);const int N=5e6+5;cp omega(LL n, LL k){ return cp(cos(2*PI*k/n),sin(2*PI*k/n));}LL n,x,len,ans[N];cp a[N],b[N];//上文的 FFT 实现省去int main(){ scanf("%d",&n); len=1; while(len<2*n)len*=2; for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x); for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x); FFT(a,len,0),FFT(b,len,0); for(int i=0;i<=len-1;i++)a[i]*=b[i]; FFT(a,len,1); for(int i=0;i<=len-1;i++)//进位 { ans[i]+=floor(a[i].real()/len+0.5); ans[i+1]+=ans[i]/10; ans[i]%=10; } int i=len; for(i;i>=0&&ans[i]==0;i--);//前导零 if(i==-1)len=0; for(;i>=0;i--)printf("%d",ans[i]); }
非递归FFT
这里有一个优化,我们发现每次递归有一个把 aiai 奇偶分开的过程,本质来看,就是将二进制末尾为 00 的数字与二进制末尾为 11 的数字分开。
我们不妨想一下,对于一个数 xx,其位置可以根据其二进制确定,就是其二进制倒过来的数字。
我们先将每个 aiai 放置在对应的位置,然后向上逐渐合并。
void FFT(cp *a,bool inv){ LL lim=0; while((1<<lim)<len)lim++; for(int i=0;i<=len-1;i++) { LL t=0; for(int j=0;j<lim;j++) if((i>>j)&1)t|=(1<<(lim-j-1));//处理其翻转后的值 if(i<t)swap(a[i],a[t]); } static cp buf[N]; for(int l=2;l<=len;l*=2) { LL m=l/2; for(LL j=0;j<=len-1;j+=l) { for(LL i=0;i<=m-1;i++) { cp x=omega(l,i+j); if(inv)x=conj(x); buf[i+j]=a[i+j]+x*a[i+j+m]; buf[i+j+m]=a[i+j]-x*a[i+j+m]; } } for(int j=0;j<=len-1;j++)a[j]=buf[j]; }}
这个东西其实就是想了个办法使得把工具人数组 buf 除掉了。
调调顺序即可。
void FFT(cp *a,bool inv){ LL lim=0; while((1<<lim)<len)lim++; for(int i=0;i<=len-1;i++) { LL t=0; for(int j=0;j<lim;j++) if((i>>j)&1)t|=(1<<(lim-j-1)); if(i<t)swap(a[i],a[t]); } for(int l=2;l<=len;l*=2) { LL m=l/2; for(LL j=0;j<=len-1;j+=l) { for(LL i=0;i<=m-1;i++) { cp x=omega(l,i+j); if(inv)x=conj(x); x*=a[i+j+m]; a[i+j+m]=a[i+j]-x; a[i+j]=a[i+j]+x; } } }}
一些小优化
对于 ii 的二进制翻转可以先预处理出来。
然后 ωknωnk 可以利用性质累乘,最后代码就长这样了:
#include<bits/stdc++.h>#define LL int#define cp complex<double>using namespace std;const double PI=acos(-1.0000);const int N=5e6+5;cp omega(LL n, LL k){ return cp(cos(2*PI*k/n),sin(2*PI*k/n));}LL n,len,lim,x,ans[N],r[N];cp a[N],b[N];void FFT(cp *a,bool inv){ for(int i=0;i<=len-1;i++) { LL t=r[i]; if(i<t)swap(a[i],a[t]); } for(int l=2;l<=len;l*=2) { LL m=l/2; cp omg=omega(l,1); for(LL j=0;j<=len-1;j+=l) { cp x(1,0); for(LL i=0;i<=m-1;i++) { cp t=x; if(inv)t=conj(t); t*=a[i+j+m]; a[i+j+m]=a[i+j]-t,a[i+j]=a[i+j]+t; x*=omg; } } }}int main(){ scanf("%d",&n); len=1; while(len<2*n)len*=2,lim++; for(int i=0;i<=len-1;i++) { LL t=0; for(int j=0;j<lim;j++)if((i>>j)&1)t|=(1<<(lim-j-1)); r[i]=t; } for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x); for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x); FFT(a,0),FFT(b,0); for(int i=0;i<=len-1;i++)a[i]*=b[i]; FFT(a,1); for(int i=0;i<=len-1;i++) { ans[i]+=floor(a[i].real()/len+0.5); ans[i+1]+=ans[i]/10; ans[i]%=10; } int i=len; for(i;i>=0&&ans[i]==0;i--); if(i==-1)len=0; for(;i>=0;i--)printf("%d",ans[i]);}
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK