

【LeetCode动态规划#05】背包问题的理论分析(基于代码随想录的个人理解,多图) - da...
source link: https://www.cnblogs.com/DAYceng/p/17258797.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

【LeetCode动态规划#05】背包问题的理论分析(基于代码随想录的个人理解,多图)
背包问题是一系列问题的统称,具体包括:01背包、完全背包、多重背包、分组背包等(仅需掌握前两种,后面的为竞赛级题目)
下面来研究01背包
实际上即使是最经典的01背包,也不会直接出现在题目中,一般是融入到其他的题目背景中再考察
因为是学习原理,所以先跳过最原始的问题模板来学。
01背包的原始题意是:(标准的背包问题)
有n件物品和一个最多能背重量为 w 的背包。第 i 件物品的重量是 weight[i] ,得到的价值是 value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
(01背包问题可以使用暴力解法,每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是O(2^n),这里的n表示物品数量。因为暴力搜索的时间复杂度是指数级别的,所以才需要通过dp来进行优化)
根据上面的描述可以举出以下例子
二维dp数组01背包
背包最大重量为4。
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
五部曲分析一波
1、确定dp数组含义
该问题中的dp数组应该是二维的,所以先定义一个dp[i][j]
该数组的含义是什么?
含义:任取编号(下标)为[0, i]之间的物品放进容量为j的背包里
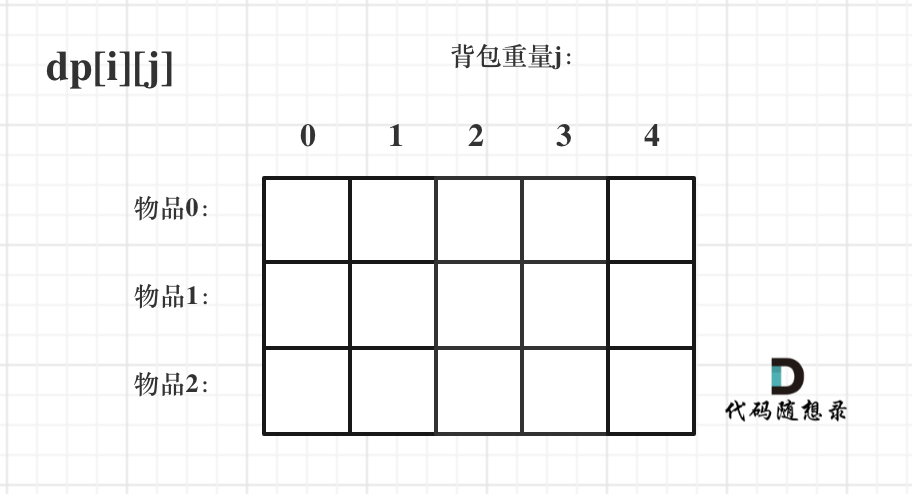
2、确定递推公式
确定递推公式之前,要明确dp[i][j]可以由哪几个方向推导出
当前背包的状态取决于放不放物品i,下面分别讨论
(1)不放物品i
dp[i - 1][j]
(2)放物品i
dp[i - 1][j - weight[i]] + value[i] (物品i的价值)
我来解释一下上面的式子是什么意思
先回顾一下dp[i][j]的含义:从下标为[0, i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有上述两个方向推出来dp[i][j]
情况1:不放物品i。此时我们已经认为物品i不会被放到背包中,那么根据dp[i][j]的定义,任取物品的范围应该变成[0, i-1]
也就是从下标为[0, i-1]的物品里任意取,放进容量为j的背包,价值总和最大是多少,即dp[i - 1][j]
再看情况2:放物品i。因为要放物品i,那就不需要再遍历到i了(相当于已经放入背包的东西下次就不遍历了)
根据dp[i][j]的定义,任取物品的范围也应该变成[0, i-1]
但是,因为情况2是要将物品i放入背包,此时背包的容量也要发生变化
根据dp[i][j]的定义,背包的容量应该要减去物品i的重量 weight[i] ,即dp[i - 1][j - weight[i]]
此时dp[i - 1][j - weight[i]]只是做好了准备放入物品i的工作,实际上物品i并没有放入,因此该式子的含义是:背包容量为j - weight[i]的时候不放物品i的最大价值
所以要再加上物品i本身的价值 value[i] ,才能求出背包放物品i得到的最大价值
即:dp[i - 1][j - weight[i]] + value[i]
根据dp[i][j]的定义,我们最后要求价值总和最大物品放入方式
因此递推公式应该是: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
从不放物品i和放物品i两个方向往dp[i][j]推,取最后结果最大的那种方式(即最优的方式)
3、确定dp数组初始化方式
可以把dp数组试着画出来,然后假设要求其中一个位置,思考可以从哪个方向将其推出,而这些方向最开始又是由哪些方向推得的,进而确定dp数组中需要初始化的部分
将本题的dp数组画出来如下:
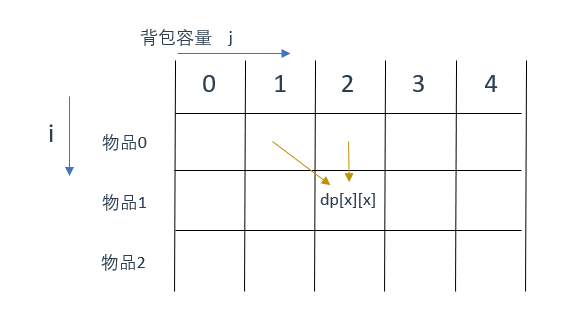
假设有一个要求的元素dp[x][x],根据前面对递推公式的讨论可知,该元素一定是由两个方向推过来求得的。
也就是情况1、情况2,那么对应到图中就是从上到下推过来的,是情况1(dp[i - 1][j])
情况2(dp[i - 1][j - weight[i]])在图中体现得不是十分确定,但是大致方向是从左上角往下推过来的
这两个方向的源头分别指向绿色区域和橙色区域
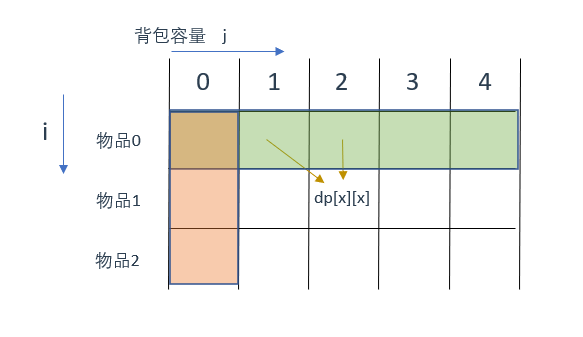
那么这两个区域就是要初始化的区域,怎么初始化呢?
先说橙色区域,从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
所以橙色区域区域需要初始化为0

再说绿色区域,状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出 i 是由 i-1 推导出来,那么 i 为 0 的时候就一定要初始化
dp[0][j],即:i 为0,存放 编号0 的物品的时候,各个容量的背包所能存放的最大价值。
很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是 value[0] ,因为背包容量放足够放编号0物品。
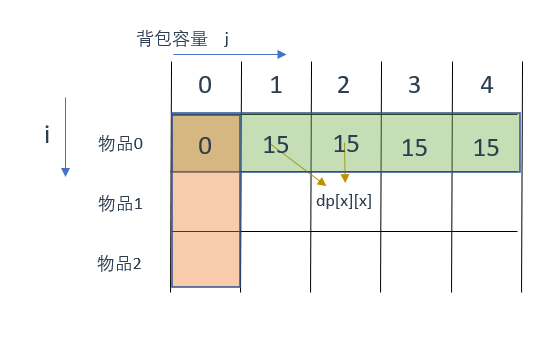
两个区域的初始化情况对应到图中如下:

初始化代码:
for (int j = 0 ; j < weight[0]; j++) { //橙色区域
dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {//绿色区域
dp[0][j] = value[0];
}
以上两个区域实际上属于“含0下标区域”,其他的“非0下标区域”也需要初始化(没想清楚为什么有时要初始化完整个dp数组,有时又不用)
“非0下标区域”初始化为任何值都可以
还是拿前面的图来看

以dp[x][x]这个位置为例,其初始化成100、200都无所谓,因为这个位置的dp值是由其上面和左上两个方向上的情况推导出来的,只取决于这里个方向最开始的初始化值。
(例如dp[x][x]这里初始化为100,我从上面推导下来之后会用推导值将100覆盖)
4、确定遍历方式
该问题中dp数组有两个维度:物品、背包容量,先遍历哪个呢?
直接说结论,都行,但是先遍历物品更好理解
(具体看代码随想录解释)
两种过程的图如下:
(这里需要重申一下背包问题的条件:每个物品只能用一次,要求的是怎么装背包里的价值最大)
先遍历物品再遍历背包容量(固定物品编号,遍历背包容量)
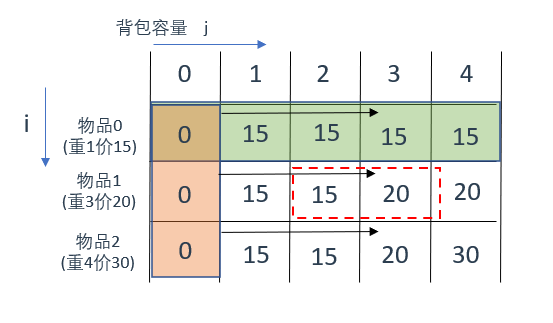
挑一个节点来说一下(图中的红框部分),此时的遍历顺序是先物后包,物品1(重3价20)在0~4种容量中放置的结果如图所示
因为固定了物品1,此时背包容量为0、1、2的情况都是放不下物品1的(又也放不下物品3),所以只能放物品0(此为最佳选择)
当遍历到背包容量为3时,可以放下物品1了,那此处的最佳选择就是放一个物品1,所以此处的dp数组值变为20
其余位置分析方法同理
先遍历背包容量再遍历物品(固定背包容量,遍历物品编号)
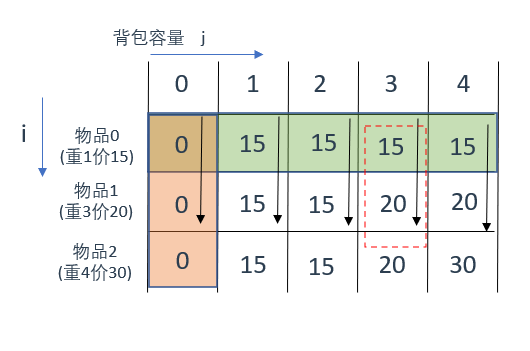
有了前面的例子,这里就很好理解了,就是从上往下遍历,固定住当前背包的容量,遍历物品,看看能不能放入,能放的话最优选择应该放哪个
还是拿红框部分来说,此时背包容量固定为3
第一次遍历,物品0可以装下,此时最优选择就是放物品0,背包总价是15;
第二次遍历,物品1可以装下,此时最优选择就是放物品1,背包总价是20;
第二次遍历,物品2装不下,此时最优选择就是放物品1,背包总价还是20;
其余位置分析方法同理
完整c++测试代码(卡哥)
void test_2_wei_bag_problem1() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK