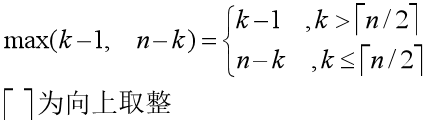线性时间选择(含平均O(n)和最坏O(n)算法) - Amαdeus
source link: https://www.cnblogs.com/MAKISE004/p/16920270.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
前言
本篇文章我将介绍 期望为线性时间 的选择算法和 最坏情况为线性时间 的选择算法,即分别为 平均情况下时间复杂度为O(n) 和 最坏情况下时间复杂度为O(n) 的线性时间选择。以下包含了我自己的全部思考和学习过程,参考书籍为 算法导论(第三版)。😊
线性时间选择问题
问题概述
线性时间选择 :一个由 n 个互异的数字构成的集合a,选择在这个集合中第 k 小的数 x,即集合中恰好有 k-1 个数字小于 x,并输出这个数字 x。
比如 我们有一个集合 {4, 2, 1, 7, 5},我们要找到集合中的第 3 小的元素,那么答案就是 4 。
解决思路
相信大部分童鞋都学习过了 快速排序算法 ,而我们的 线性时间选择算法 就是基于快速排序的。(如有对快速排序还不了解的童鞋,可以来看看这里哟~ 快速排序)🥰🥰🥰
在线性时间选择算法中,我们会延用快速排序中使用到的划分函数 Partition,我们将用这个 Partition 函数来递归划分数组。与快速排序不同的是,我们在调用这个 Partition 函数的时候,只会对数组的其中一边进行不断划分,而快速排序需要对两边都不断进行划分,最后得到正序序列。
在后面的分析中我们会发现,我们选择的第 k 小的元素,可能就是当前这个划分位置对应的元素,如果不在当前划分位置,要么就是在数组划分处的左半部分,要么就是在数组划分处的右半部分。所以我们只需要对一边进行操作,不断去判断当前划分位置的元素是否是我们要找的第 k 小元素 x 即可。
平均情况为O(n)的线性时间选择
算法步骤
1、我们将 Partition 函数进行一个小小的改进,采用随机取基准值的方式对数组进行划分,即 Randomized-Partition ,这样有可能避免一些极端的划分情况。(Partition 在后续的实现代码中,我将使用左右指针法)
2、得到当前基准值的划分位置 mid,定义一个 res 记录当前这个元素在 [left, right] 范围中是第几小元素。
3、如果 k == res,那么这个这个划分位置的元素就是我们要找的第 k 小的元素。
如果不是,有以下两种情况:
当 k < res 时,我们要从当前 [left, right] 的左半部分进行寻找,即 [left, mid - 1]。不难发现,之后我们依旧找的是此范围的第 k 小元素。
当 k > res 时,我们要从当前 [left, right] 的右半部分进行寻找,即 [mid + 1, right],但是要注意的是,对于整个集合范围的第 k 小元素,此时我们要找的应该是 [mid + 1, right] 中的第 k - res 小元素。🥺
程序实现
1|0源代码
#include<iostream> #include<algorithm> #include<ctime> using namespace std;
//原始划分函数 int Partition(int a[], int left, int right){ int i = left; int j = right; int key = a[left];
while(i != j){ while(i < j && a[j] >= key) //向左找到小于基准值的值的下标 j--; while(i < j && a[i] <= key) //向右找到大于基准值的值的下标 i++; swap(a[i], a[j]); } /* i等于j时跳出循环 当前基准值此时在下标为i的位置(合适的位置) */ swap(a[left], a[i]); //最左边的元素变为处于当前合适位置的元素,把基准值放在合适位置 return i; //返回合适位置(i,j都可以) }
//随机取基准值 划分函数 int Randomized_Partition(int a[], int left, int right){ int random = rand() % (right - left + 1) + left; swap(a[random], a[left]);
return Partition(a, left, right); }
//平均情况O(n²)的线性时间选择 int Randomized_Select(int a[], int left, int right, int k){ if(left == right) return a[left];
int mid = Randomized_Partition(a, left, right); int res = mid - left + 1; //res表示当前是范围内的第几小 if(k == res) return a[mid]; if(k < res) return Randomized_Select(a, left, mid - 1, k); else return Randomized_Select(a, mid + 1, right, k - res); }
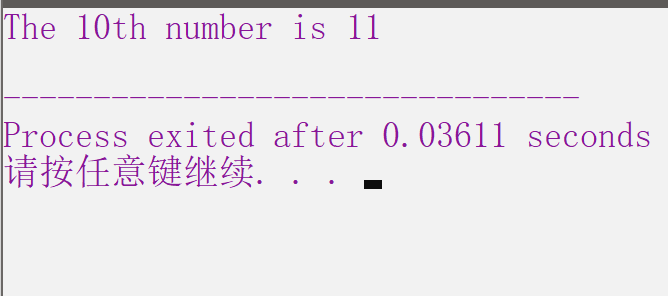
main(){ int a[27] = {25,11,9,1,13,21,3,10,27,15,19,8,30,35,22,12,31,2,7,23,26,5,14,37,4,34,17}; cout<<"The 10th number is "<<Randomized_Select(a, 0, 26, 10)<<endl; /* 作者 Amαdeus */ }
1|0运行结果图
时间复杂度分析
1|0最坏时间复杂度
假如我们每次划分的位置的元素恰好每次都不是当前的第 k 小元素,我们要进行 n - 1 的划分,而划分的时间复杂度为 O(n),所以我们可以得到此时的最坏时间复杂度为 O(n²) 。举个简单一点的例子,假如我们要找的是当前集合中的最小的元素,即第 1 小元素,若我们每次划分的位置的元素恰好是当前范围内的最大元素,那么可想而知我们的最坏时间复杂度就是 O(n²) 。
1|0平均时间复杂度
现在我们重点分析随机取基准值的线性时间选择的平均时间复杂度,即如何求得平均时间复杂度为 O(n)。🤔
在分析过程中,我们需要用到一些概率论的知识(概率论好难的额😭😭😭)。
我们可以假设这个算法在数组 a[left ... right] 上运行的时间是一个随机变量,记作 T(n) 。我们视每一次划分返回的基准值是等可能性的,由此我们可以得到对于每一个 k (0<k<=n),子数组 a[left, mid]恰好有 k 个元素小于基准值的概率为 1/n。我们可以得到下列关系式:
现在我们具体计算 T(n):
假设 T(n) 是单调递增的,我们可以评估得到其递归调用所需的上界。而对于我们之前设的随机变量 Xk,当 k 与 Xk 相对应时,Xk 取 1 ,在其他情况下都是取 0。当 Xk = 1 时,我们有可能要处理的是最半部分长度为 k - 1 的数组,也有可能是右半部分长度为 n - k 的数组,为了得到 T(n) 的上界,我们需要取两种可能中的较大时间。同时不要忘了划分本身消耗的时间。由此我们可以得到如下的关系式:
我们可以很容易发现,当 n 为偶数时,T(n/2) 到 T(n-1) 都各自出现了两次;如果 n 为奇数呢,除了偶数情况下各自出现两次之外,还有一个 T((n-1)/2) 出现了一次,但是并不影响上界的证明。我们总结之前得到的关系式,可以得到以下不等式:
此时,E(T(n)) 最多是 cn,当常数 c > 4a 时,n >= 2c/(c-4a)。由此可以得到,当 n < 2c/(c-4a) 时,T(n) = O(1),这就满足了我们在上面图中做出的存在常数时间复杂度的假设;同时,因为 E(T(n)) 最多是 cn,我们的常数 c 也存在,那么期望时间复杂度 E(T(n)) = O(n)。
综上,随机取基准值的线性时间选择的平均时间复杂度为 O(n)。
分析过程中的思考
1|0为什么 E(Xk) 与 T(max(k-1, n-k)) 相互独立
注意 Xk 表示的是子数组 a[left, mid] 恰好有 k 个元素的概率,而我们所设的 T(n) 是在这个长度的子数组上操作所运行的时间,这两者是有本质上差别的。通俗地来讲,我们可以把子数组 a[left, mid] 看成是长度为 mid-left+1 的一列地砖,地砖上只有前 k 个上有数字,我们现在要从当前起点匀速走过这些地砖,不会去看这些数字是什么和多少个,那么我们走过去的时间一定是一个常量,即我们走过去的时间就是速度×地砖长度。可见 Xk 和 T(n) 是毫不相干的两个量,所以自然是相互独立地咯~。
最坏情况为O(n)的线性时间选择
算法思考
先前我们已经知道了平均情况下时间复杂度为 O(n) 的线性时间选择算法,但是它的最坏时间复杂度是 O(n²),那么是否有方法可以使最坏时间复杂度降低到 O(n) 呢?🧐
接下来将介绍所谓的 最坏情况为O(n) 的选择算法,Select 选择算法。
算法步骤
1、我们将集合中的元素进行每 5 个进行分组,剩余于的 n mod 5 个元素组成单独一个组;
2、对每一组单独进行排序(比较简单的排序方式都可以),取出每一组的中位数,并和序列的前几个进行交换(为了后期方便);
3、将取出的所有组的中位数,递归调用 Select 函数,找出所有中位数的中位数 x;
4、按照这个中位数 x,对当前 [left, right] 范围序列进行划分;
5、定义 res = mid - left + 1 判断是否是当前的第 k 小元素,若是直接返回 a[mid];
否则,有以下两种情况:
若 k < res,就在左半部分递归调用 Select 函数,寻找 [left, mid - 1] 内的第 k 小元素;
若 k > res,就在右半部分递归调用 Select 函数,寻找 [mid + 1, right] 内的第 k-res 小元素。
动态演示
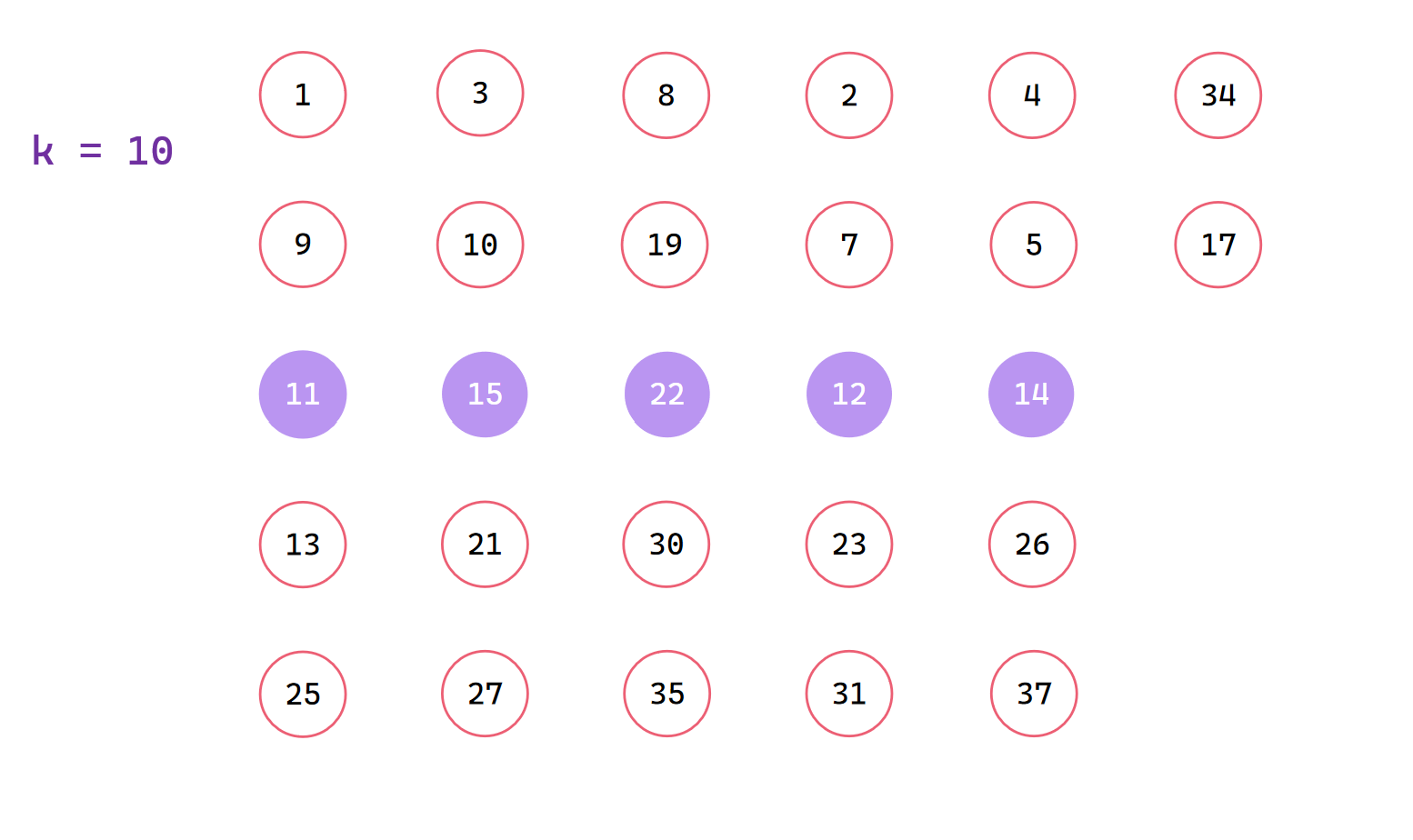
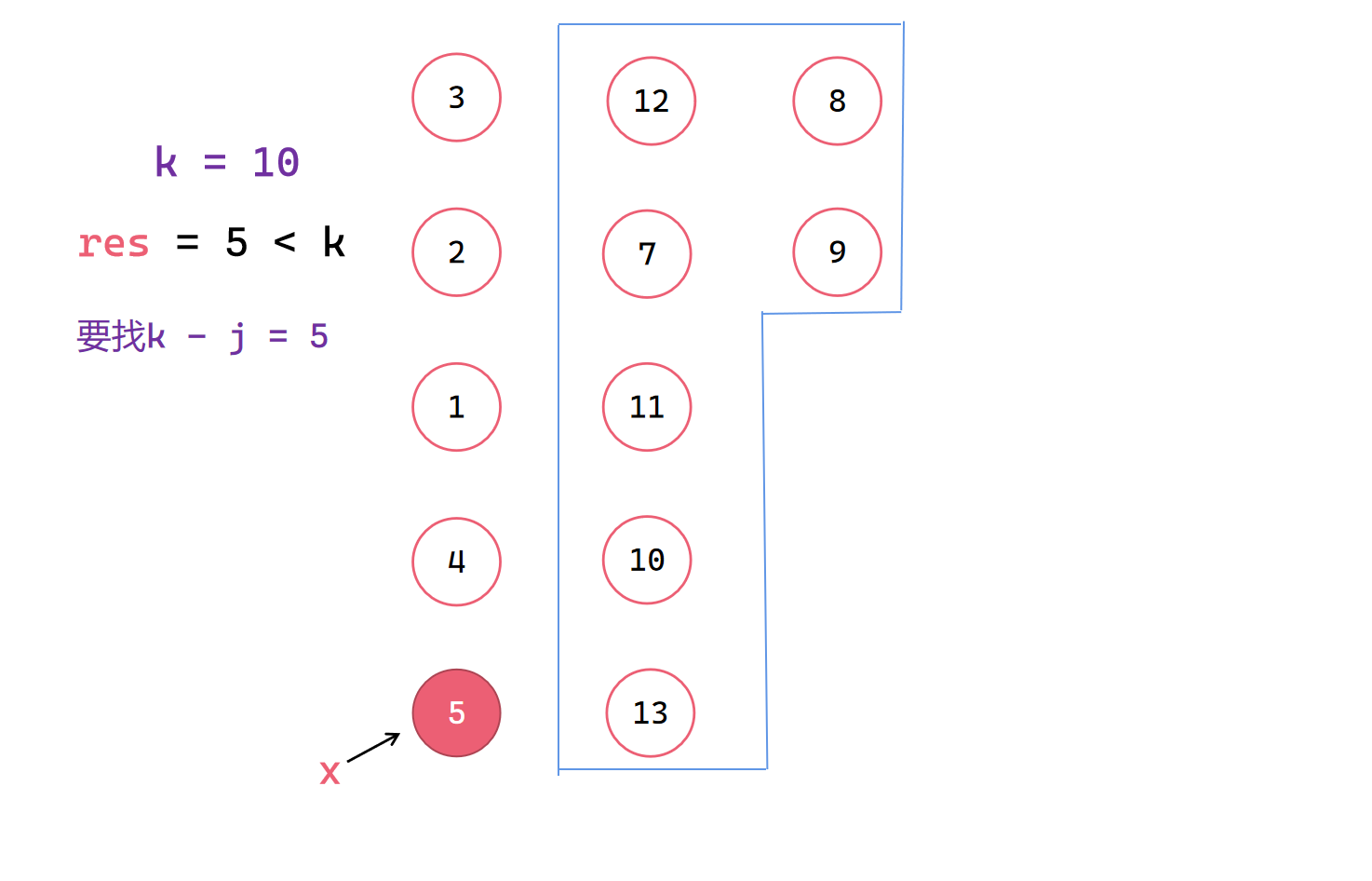
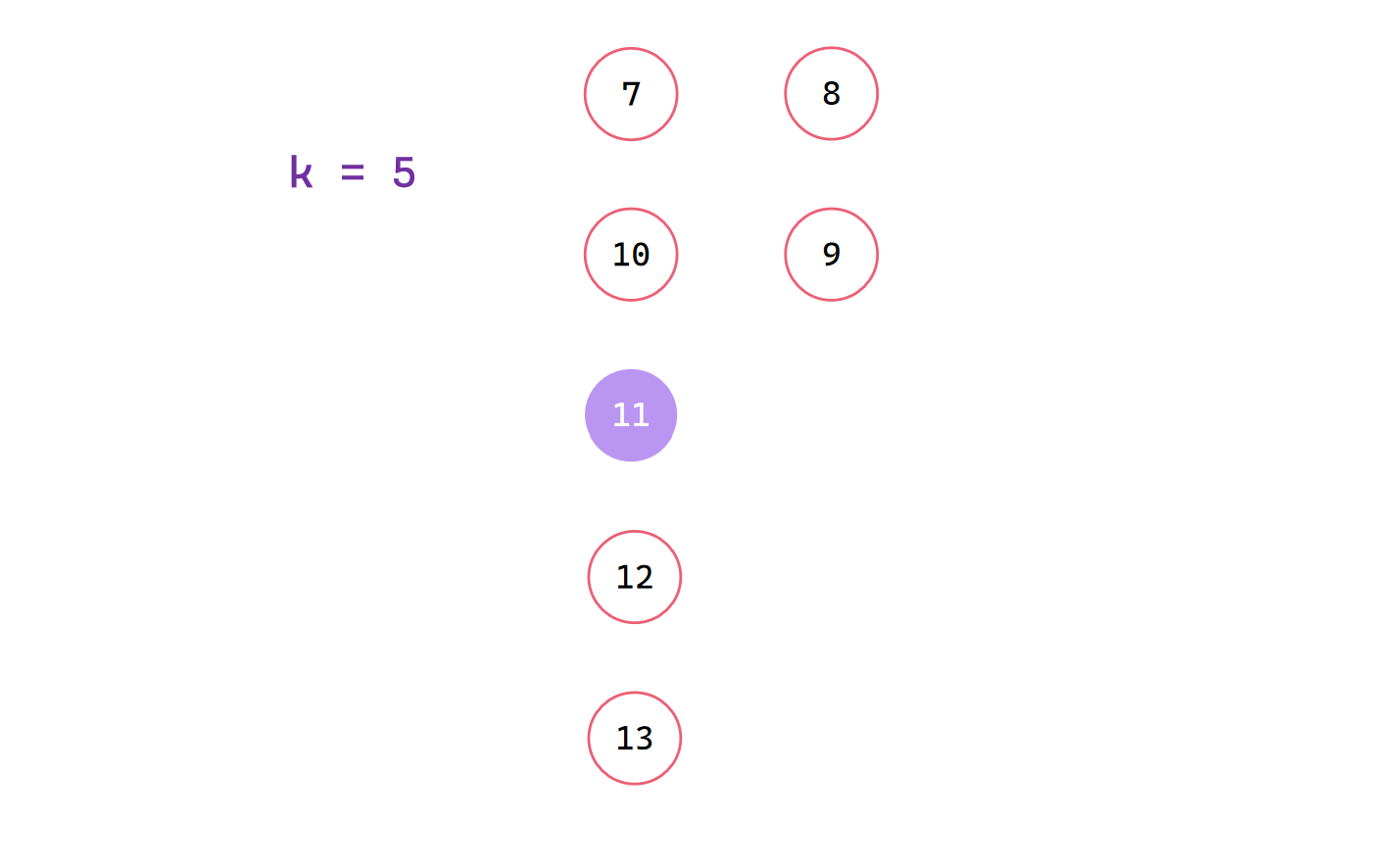
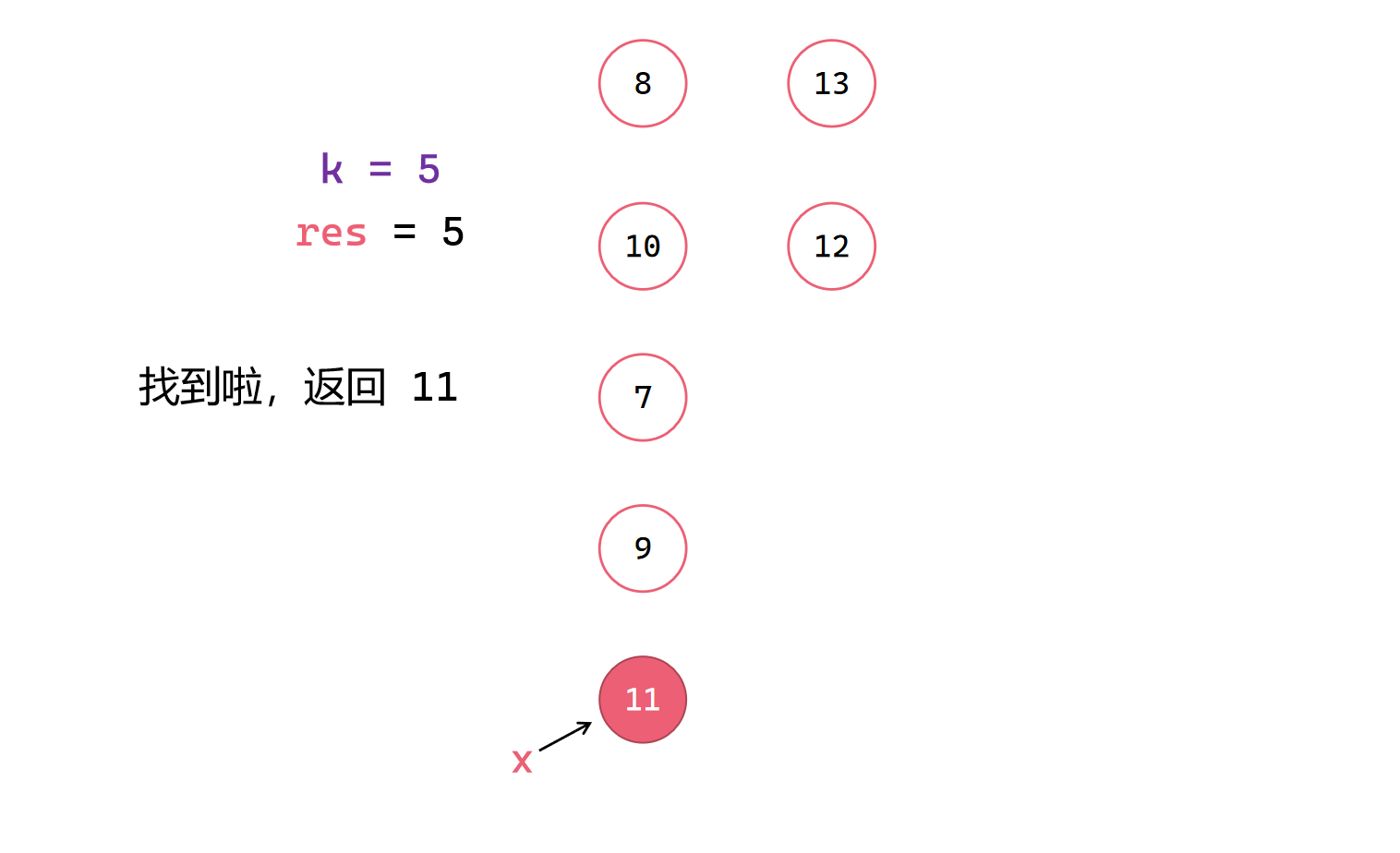
我们以集合 a[27] = {25,11,9,1,13,21,3,10,27,15,19,8,30,35,22,12,31,2,7,23,26,5,14,37,4,34,17}, k = 10为例
1|0初始元素,从左到右每五个分一组
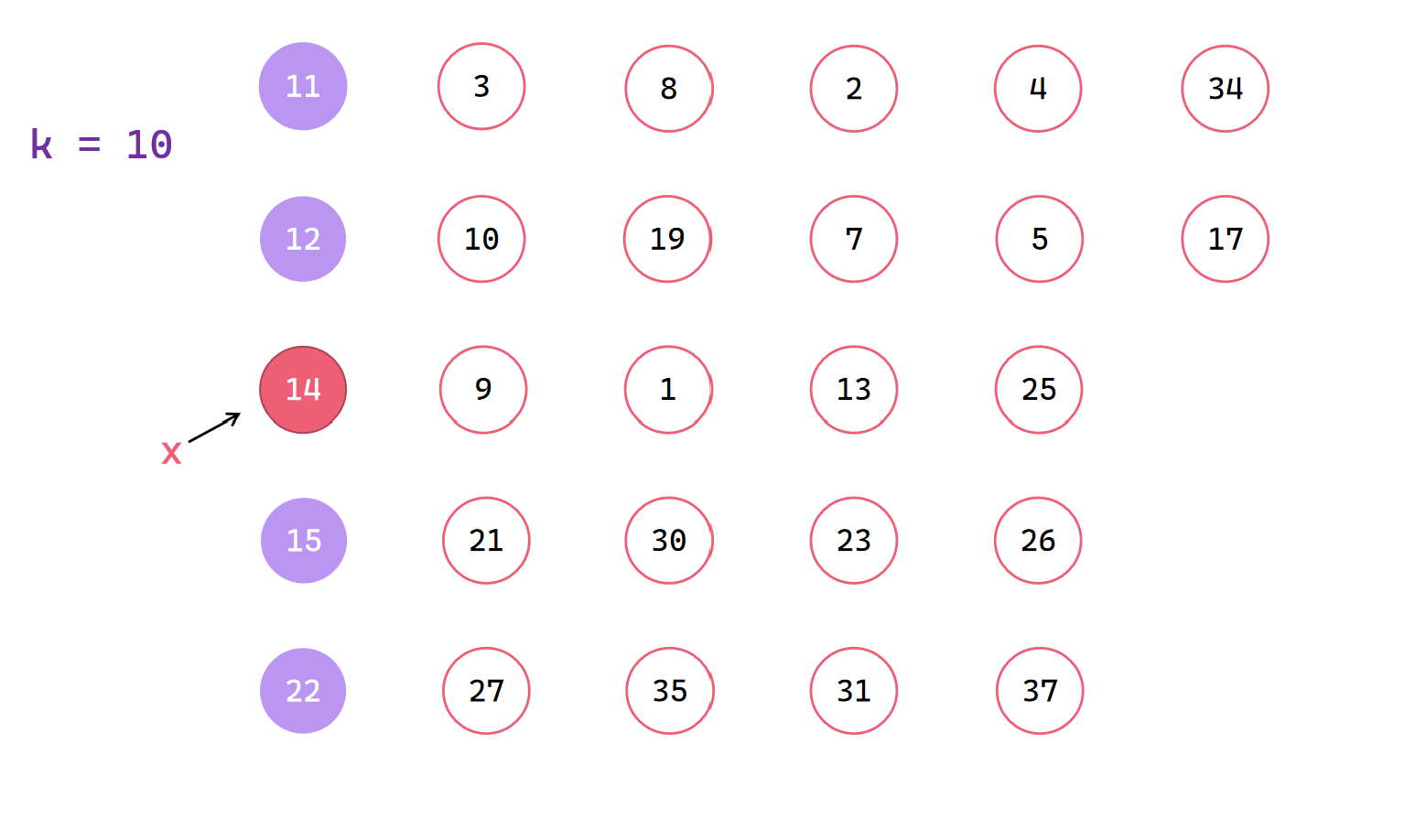
1|0每组排序找到中位数,最后一组不处理
1|0中位数和前面交换,找出中位数的中位数x
1|0按照x进行划分并判断
1|0递归调用找左半部分并找出中位数
1|0中位数和前面交换,找出此时的x
1|0中位数的中位数x进行划分
1|0递归调用找右半部分并找出中位数
1|0此时中位数就一个,作为x进行划分找到第10小元素
程序实现
1|0源代码
#include<iostream> #include<algorithm> #include<ctime> using namespace std;
//最坏情况O(n)的线性时间选择 划分函数 int Partition(int a[], int left, int right, int x){ //找到基准值并和第一个位置交换 for(int index = left; index <= right; index++){ if(a[index] == x){ swap(a[index], a[left]); break; } } //找到基准值位置确定划分处(左右指针法) int i = left, j = right; while(i != j){ while(i < j && a[j] >= x) j--; while(i < j && a[i] <= x) i++; swap(a[i], a[j]); } swap(a[left], a[i]); return i; }
//最坏情况O(n)的线性时间选择 int Select(int a[], int left, int right, int k){ //当小于五个元素时直接进行C++自带排序(其他排序方式也可以) if(right - left < 5){ sort(a + left, a + right + 1); //记得sort左闭右开 return a[k + left - 1]; }
//每五个一组,找到各组中位数,并存储到前(r-l-4)/5的位置 for(int i = 0; i <= (right - left - 4)/5; i++){ //当前 有(r-l-4)/5向下取整+1个 中位数 sort(a + left + i * 5, a + left + i*5 + 4 + 1); //每组的中位数交换到前面 swap(a[left + i], a[left + i*5 + 2]); }
//递归调用Select找出所有中位数的中位数 x int x = Select(a, left, left + (right-left-4)/5, (right-left-4)/10 + 1);
//以 x 为基准值找到所在的划分位置 int mid = Partition(a, left, right, x); int res = mid - left + 1; if(k == res) return a[mid]; //找到第 k 小该元素 if(k < res) return Select(a, left, mid - 1, k); //继续在左半部分寻找 else return Select(a, mid + 1, right, k - res);//继续在右半部分寻找 }
main(){ int a[27] = {25,11,9,1,13,21,3,10,27,15,19,8,30,35,22,12,31,2,7,23,26,5,14,37,4,34,17}; cout<<"第 10 小元素为: "<<Select(a, 0, 26, 10)<<endl;
/* 作者 Amαdeus */ }
1|0运行结果图
时间复杂度分析
1|0最坏情况时间复杂度
我们需要求得最坏时间复杂度,就是需要求得这个时间复杂度 T(n) 的上界。在确定了一个划分基准值 x 时,我们不难发现,这个时候的 n/5向上取整 组中,除了那个不满五个元素的组 和 x 自己所在的组,我们至少有一半的组有 三个元素 大于 x。那么减去这两个特殊的组,只算那至少一半的组,我们可以得到大于 x 的元素的个数如下:
那么由这个上界,在之前的 算法步骤 5 中,我们递归调用的最大时间是 T(7n/10 + 6) 。
这个时候我们整理一下每个步骤需要的时间:
首先,之前的 算法步骤 1 中,我们分组的时间复杂度很明显是 O(n);
其次 算法步骤 2 对每组的五个元素进行排序,我们视其为对相对于整个问题(可以把整个问题看成有非常多的元素,例如一亿个数据)为 O(1) 规模大小的每组进行排序,对此我们要进行 O(n) 时间复杂度次数的排序,那么我们在此步骤中相对于整个问题而言时间复杂度也是同级的O(n);
然后是 算法步骤 3,递归调用 Select,以为有 n/5向上取整 个中位数,显然我们要消耗 T(n/5向上取整);
那么综合上面的几个时间复杂度,我们可以得到如下关系式:
现在我们要再次用到先前在 平均情况O(n)的线性时间选择 板块所用到的假设法来证明这个关系式最后解出的 T(n) 是线性的。🤔
我们假设存在足够大的常数 c 使得对所有 n>0 有 T(n)<=cn,还要假设某个小于常数的 n 使得T(n) = O(1);同时还需要选择一个常数 a,使得对所有 n>0,关系式中的 O(n) 存在上界 an。由此我们可以得到如下不等式:
综上,我们可以得到当前算法的 最坏时间复杂度 为 O(n),也许上面的证明有一些颠覆人们的认知,然后事实就是如此。😉
程序改进
1|0程序改进点
我们在上面得到了当 n > 70 时的时间复杂度为 O(n);当 n <= 70 的时候只要 O(1) 的时间。
当我们解决问题的规模非常大时,假如有100000个互异的元素,我们不妨定一个数字,若当前数组范围小于这个数字时,直接进行简单的排序,返回这个第 k 小的元素。我们之前得到的 n < 70,那么我们可以用一个与之相近并大于它的数字来替代这个 70,就比如 75 吧。当数据规模小于 75 时,我们直接进行排序即可。
1|0改进程序源代码
下面是改进后的实现代码,测试用例规模 100000 。对于元素互异的问题,我们由于数据量较大,所以可以假设元素都是互异的。
#include<iostream> #include<algorithm> #include<ctime> using namespace std;
//最坏情况O(n)的线性时间选择 划分函数 int Partition(int a[], int left, int right, int x){ //找到基准值并和第一个位置交换 for(int index = left; index <= right; index++){ if(a[index] == x){ swap(a[index], a[left]); break; } } //找到基准值位置确定划分处(左右指针法) int i = left, j = right; while(i != j){ while(i < j && a[j] >= x) j--; while(i < j && a[i] <= x) i++; swap(a[i], a[j]); } swap(a[left], a[i]); return i; }
//最坏情况O(n)的线性时间选择 int Select(int a[], int left, int right, int k){ //当g规模小于 75 时直接进行排序(其他排序方式也可以) if(right - left < 75){ sort(a + left, a + right + 1); //记得sort左闭右开 return a[k + left - 1]; }
//每五个一组,找到各组中位数,并存储到前(r-l-4)/5的位置 for(int i = 0; i <= (right - left - 4)/5; i++){ //当前 有(r-l-4)/5向下取整+1个 中位数 sort(a + left + i * 5, a + left + i*5 + 4 + 1); //每组的中位数交换到前面 swap(a[left + i], a[left + i*5 + 2]); }
//递归调用Select找出所有中位数的中位数 x int x = Select(a, left, left + (right-left-4)/5, (right-left-4)/10 + 1);
//以 x 为基准值找到所在的划分位置 int mid = Partition(a, left, right, x); int res = mid - left + 1; if(k == res) return a[mid]; //找到第 k 小该元素 if(k < res) return Select(a, left, mid - 1, k); //继续在左半部分寻找 else return Select(a, mid + 1, right, k - res);//继续在右半部分寻找 }
int *a = new int[1000 * 100]; //全局变量,防止栈溢出 main(){ srand((int)time(0)); int index = 0; while(index < 100000){ int num = rand() % RAND_MAX * (rand() % 100); //生成大随机数 a[index++] = num; }
for(int i = 0; i < 100000; i++) cout<<a[i]<<" "; cout<<endl<<endl;
cout<<"第 66666 小元素为: "<<Select(a, 0, 99999, 66666)<<endl;
/* 作者 Amαdeus */ }
1|0程序运行结果图
__EOF__
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK