支持向量机系列五：Numerical Optimization

原文链接请点击这里

作为支持向量机系列的基本篇的最后一篇文章，我在这里打算简单地介绍一下用于优化 dual 问题的 Sequential Minimal Optimization (SMO) 方法。确确实实只是简单介绍一下，原因主要有两个：第一这类优化算法，特别是牵涉到实现细节的时候，干巴巴地讲算法不太好玩，有时候讲出来每个人实现得结果还不一样，提一下方法，再结合实际的实现代码的话，应该会更加明了，而且也能看出理论和实践之间的差别；另外（其实这个是主要原因）我自己对这一块也确实不太懂。先回忆一下我们之前得出的要求解的 dual 问题：

maxαn∑i=1αi–12n∑i,j=1αiαjyiyjκ(xi,xj)s.t.,0≤αi≤C,i=1,…,nn∑i=1αiyi=0

对于变量 α 来说，这是一个 quadratic 函数。通常对于优化问题，我们没有办法的时候就会想到最笨的办法——Gradient Descent ，也就是梯度下降。注意我们这里的问题是要求最大值，只要在前面加上一个负号就可以转化为求最小值，所以 Gradient Descent 和 Gradient Ascend 并没有什么本质的区别，其基本思想直观上来说就是：梯度是函数值增幅最大的方向，因此只要沿着梯度的反方向走，就能使得函数值减小得越大，从而期望迅速达到最小值。当然普通的 Gradient Descent 并不能保证达到最小值，因为很有可能陷入一个局部极小值。不过对于 quadratic 问题，极值只有一个，所以是没有局部极值的问题。

另外还有一种叫做 Coordinate Descend 的变种，它每次只选择一个维度，例如α=(α1,…,αn)，它每次选取αi 为变量，而将α1,…,αi−1,αi+1,…,αn都看成是常量，从而原始的问题在这一步变成一个一元函数，然后针对这个一元函数求最小值，如此反复轮换不同的维度进行迭代。Coordinate Descend 的主要用处在于那些原本很复杂，但是如果只限制在一维的情况下则变得很简单甚至可以直接求极值的情况，例如我们这里的问题，暂且不管约束条件，如果只看目标函数的话，当α只有一个分量是变量的时候，这就是一个普通的一元二次函数的极值问题，初中生也会做，带入公式即可。

然而这里还有一个问题就是约束条件的存在，其实如果没有约束条件的话，本身就是一个多元的 quadratic 问题，也是很好求解的。但是有了约束条件，结果让 Coordinate Descend 变得很尴尬了：比如我们假设 α1是变量，而α2,…,αn是固定值的话，那么其实没有什么好优化的了，直接根据第二个约束条件∑ni=1αiyi=0，α1的值立即就可以定下来——事实上，迭代每个坐标维度，最后发现优化根本进行不下去，因为迭代了一轮之后会发现根本没有任何进展，一切都停留在初始值。

所以 Sequential Minimal Optimization (SMO) 一次选取了两个坐标维度来进行优化。例如（不失一般性），我们假设现在选取α1和 α2为变量，其余为常量，则根据约束条件我们有：

n∑i=1αiyi=0⇒α2=1y2(n∑i=3αiyi−α1y1)≜y2(K−α1y1)

其中那个从 3 到 n 的作和由于都是常量，我们统一记作K，然后由于y∈{−1,+1}，所以y2和1/y2是完全一样的，所以可以拿到分子上来。将这个式子带入原来的目标函数中，可以消去α2，从而变成一个一元二次函数，具体展开的形式我就不写了，总之现在变成了一个非常简单的问题：带区间约束的一元二次函数极值问题——这个也是初中就学过求解方法的。唯一需要注意一点的就是这里的约束条件，一个就是α1本身需要满足0≤α1≤C，然后由于α2也要满足同样的约束，即：

0≤y2(K−α1y1)≤C

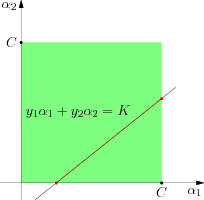
也可以得到α1的一个可行区间，同[0,C]交集即可得到最终的可行区间。这个问题可以从图中得到一个直观的感觉。原本关于α1 和α2的区间限制构成途中绿色的的方块，而另一个约束条件y1α1+y2α2=K实际上表示一条直线，两个集合的交集即是途中红颜色的线段，投影到α1轴上所对应的区间即是α1的取值范围，在这个区间内求二次函数的最大值即可完成 SMO 的一步迭代。

同 Coordinate Descent 一样，SMO 也会选取不同的两个 coordinate 维度进行优化，可以看出由于每一个迭代步骤实际上是一个可以直接求解的一元二次函数极值问题，所以求解非常高效。此外，SMO 也并不是依次或者随机地选取两个坐标维度，而是有一些启发式的策略来选取最优的两个坐标维度，具体的选取方法（和其他的一些细节），可以参见 John C. Platt 的那篇论文 Fast Training of Support Vector Machines Using Sequential Minimal Optimization 。关于 SMO ，我就不再多说了。如果你对研究实际的代码比较感兴趣，可以去看 LibSVM 的实现，当然，它那个也许已经不是原来版本的 SMO 了，因为本来 SVM 的优化就是一个有许多研究工作的领域，在那些主要的优化方法之上，也有各种改进的办法或者全新的算法提出来。

除了 LibSVM 之外，另外一个流行的实现 SVMlight 似乎是用了另一种优化方法，具体可以参考一下它相关的论文 Making large-Scale SVM Learning Practical 。

此外，虽然我们从 dual 问题的推导中得出了许多 SVM 的优良性质，但是 SVM 的数值优化（即使是非线性的版本）其实并不一定需要转化为 dual 问题来完成的，具体做法我并不清楚，不过这方面的文章也不少，比如 2007 年 Neural Computation 的一篇 Training a support vector machine in the primal 。如果感兴趣可以参考一下。 😄

张驰原，网络 id pluskid，MIT 计算机博士在读，假装的 Julia 语言爱好者。