共轭梯度法计算回归 | 统计之都

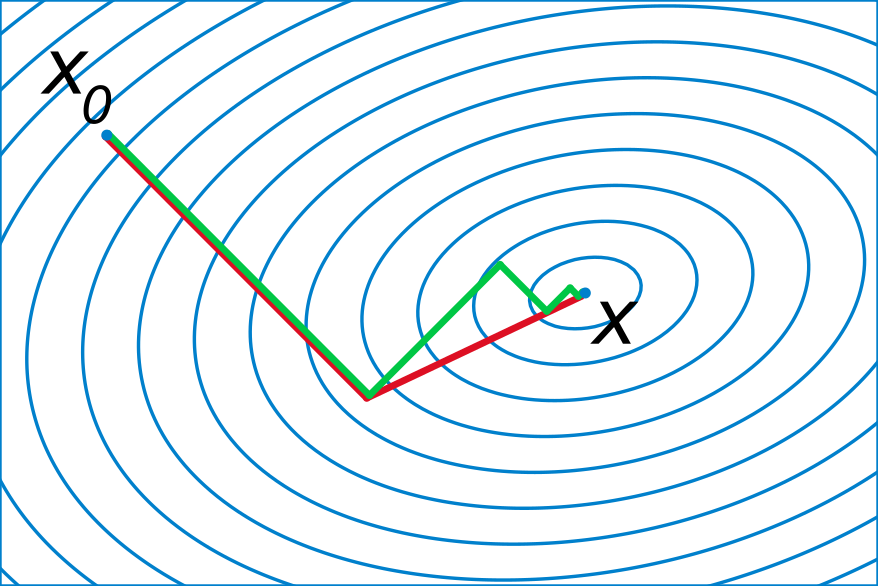
共轭梯度示意图（图片来源：维基百科）

轮回眼共轭梯度示意图（图片来源：维基百科）

之所以写这篇文章，是因为前几天统计之都的微信群里有同学提了一个问题，想要对一个很大的数据集做回归。然后大家纷纷给出了自己的建议，而我觉得共轭梯度算回归的方法跟这个背景比较契合，所以就正好写成一篇小文，与大家分享一下。

说到算回归，或许大家都会觉得这个问题太过简单了，如果用 X 表示自变量矩阵，y 表示因变量向量，那么回归系数的最小二乘解就是 ˆβ=(X′X)−1X′y。（本文完）

哎等等，别真走啊，我们的主角共轭梯度还没出场呢。前面的这个算系数的公式确实非常简洁、优雅、纯天然、不做作，但要往里面深究的话，还是有很多问题值得挖掘的。

最简单暴力的方法，就是从左向右，依次计算矩阵乘法，矩阵求逆，又一个矩阵乘法，最后是矩阵和向量的乘法。如果你就是这么算的，那么可以先默默地去面壁两分钟了。

更合理的方法，要么是对 X′X 进行 Cholesky 分解，要么是对 X 进行 QR 分解，它们基本上是现在算回归的软件中最常见的方法。关于暴力方法和矩阵分解方法的介绍和对比，可以参见这个 B 站上的视频。（什么？你问我这么严肃的话题为什么要放 B 站上？因为大部分时间都是在吐槽啊）

好，刚才去面壁的同学现在应该已经回来了，我们继续。前面这些通过矩阵运算求回归系数的方法，我们可以统称为直接法。叫这个名字，是因为它们都可以在确定数目的步骤内得到最终的结果。而与之相对的，则叫做迭代法，意思是通过不断更新已经得到的结果，来逐渐逼近真实的取值。打个比方，你想要知道一瓶 82 年的拉菲值多少钱，直接法就是去做调研，原料值多少，品牌值多少，加工费多少，运输费多少…… 然后加总起来得到最终的定价；而迭代法就是去问酒庄老板，你先随便蒙一个数，然后老板告诉你高了还是低了，反复循环，总能猜个八九不离十。

说到这里，你自然要问了，既然算回归的软件大都是用直接法，为什么还要考虑迭代法？莫非直接法有什么不好的地方？这就说到问题的点子上了。

首先，如果我们假设数据有 n 行 p 列，那么我们会发现，X′X 的维度就是 p×p，而如果变量数特别多，那么这个矩阵就会以平方的速度增大，那时候不要说算矩阵分解，即使是要存储这个大矩阵，可能都会遇到很多麻烦。

第二点，往好的方面讲，直接法给出的结果精度一般非常高，但在许多实际问题中，可能小数点后面三位保证正确就足够了，而直接法可能会为了保证十三位的精度而多出非常多的计算量。用直接法得到高精度的结果，再舍入成低精度的实际需求，总有一种买椟还珠的感觉。相反，迭代法是一个向真相逐渐靠近的过程，如果在中途已经可以保证需要的精度，那么就随时可以停止，节省计算时间。

第三点就更偏技术层面一点。通常而言，如果数据很大，那么很有可能矩阵 X 会带有某种稀疏特性，也就是说其中会有非常多的零元素。稀疏矩阵具有一些高效的存储方法和矩阵运算算法，但用直接法得到 X′X 之后，它就往往不再是稀疏矩阵了，于是存储量和计算量都会陡增。换言之，本来具有计算优势的稀疏矩阵，在直接法中却并不能发挥出它的优势来。

那么是不是有某种迭代法可以克服这些缺点呢？巧的是，本文要介绍的共轭梯度法就是其中之一。（哎说实话写这句的时候我自己都不信有多巧，前面铺垫这么多 + 设问句 + 巧合明显是作者刻意安排的啊，太明显了……）

什么是共轭梯度法？

共轭，其实是线性代数里面的一个概念。给定一个正定矩阵 A，如果两个向量 u 和 v 满足 u′Av=0，就说 u 和 v 是关于 A 共轭的。一个 m×m 的正定矩阵，最多可以有 m 组相互共轭的向量，而它们就组成了 m 维向量空间里的一组基 {p1,p2,…,pm}。通过线性代数的知识我们知道，给定了一组基后，向量空间里的任何一个元素就可以写成这组基的线性组合，比如

x=m∑i=1αipi.

在回归模型中，回归系数 ˆβ 正是线性方程组 Ax=b 的解，其中 A=X′X，b=X′y。而共轭梯度法（Conjugate gradient, CG），就是想像上面这个式子一样，把解 x 表达成共轭向量基的线性组合：只要依次算出所有的共轭向量 pi 和对应的系数 αi，就可以得出 x。而在实际情况中，有可能用更少数目的 pi 就能得到对 x 的良好近似，于是在这个意义上 CG 就是一种迭代法了。

那么为什么要叫共轭 “梯度” 呢？这是因为前面的这个公式还有另一种理解。考虑一个函数 f(x)=12x′Ax−b′x，我们很容易发现它取最小值的点正是方程 Ax=b 的解。如果我们用最优化的思路去解 Ax=b，就是要找到一个 x 使得 f(x) 达到最小。一般情况下，我们会采用 “最速下降” 的算法，即给定一个初始值 x0，计算当前的梯度，然后沿着该梯度方向移动到下一个更新值 x1，再计算梯度，如此反复循环。而共轭梯度法，则是说我们并不是沿着梯度走，而是沿着所谓的 “共轭梯度”，即 pi，进行移动。

至于为什么应该用共轭梯度而不是梯度，我建议感兴趣的读者看一看文章最后的那篇参考文献，其中对共轭梯度的优势进行了非常详细的阐述。一个直观的理解就是，普通的梯度法往往会有重复移动的方向（如文首图片中的绿线），而共轭梯度保证了每次移动的方向是共轭的（即关于 A 是正交的，如文首图片中的红线），因此不会有重复的劳动。关于 CG 的理论说来那个话就长了，因此本文不在这方面做过多的论述（其实是因为作者太懒），我在这里更想强调的其实是它的计算过程，参见图 1。

图 1：共轭梯度法算法流程

神奇在哪里？

图 1 所示的算法基本上可以展现出 CG 最重要的几个特性。

首先第一点，从图 1 可以看出，与 A 有关的运算只是一个矩阵乘法 Apk，剩下的部分都是向量之间的运算，没有任何其他更复杂的操作。而我们知道，矩阵与向量的乘法是很容易编程实现的，而且即使当矩阵很大的时候，它的内存占用量也非常小。纵观整个算法，基本上只需要存储若干个向量，所以在这个层面上，共轭梯度法非常适合内存受限的情形。

然后第二点，就如之前所说，共轭梯度法是一种迭代法，但它最奇特的一点在于，它同时又能保证在 m 步内完成计算。所以从某种层面上说，它兼具了直接法和迭代法的优点，好的情形下可以提前终止，最差的情况也能在 m 步内完成。

第三点，由于共轭梯度法中的大矩阵只参与乘法运算，所以稀疏矩阵的高效算法就可以派上用场了。可能你会说，A=X′X 不是已经破坏了稀疏性了吗？但实际上，在计算 Apk 的时候，可以先计算 v=Xpk，再计算 Apk=X′v，这样两步分开来都是稀疏矩阵的运算。

如前所说，CG 的一大优势在于编程实现非常简单。不依赖于任何附加包，我们就可以用几十行 R 代码搞定其核心算法。

## Target: solve linear equation Ax = b. A is positive definite
## Ax      -- A function to calculate the matrix-vector product
##            `A * x` given a vector `x` as the first argument
## b       -- Vector of the right hand side of the equation
## x0      -- Initial guess of the solution
## eps     -- Precision parameter
## verbose -- Whether to print out iteration information
cg = function(Ax, b, x0 = rep(0, length(b)), eps = 1e-6,
              verbose = TRUE, ...)
{
    m = length(b)
    x = x0
    r = b - Ax(x0, ...)
    p = r
    r2 = sum(r^2)
    for(i in 1:m)
    {
        Ap = Ax(p, ...)
        alpha = r2 / sum(p * Ap)
        x = x + alpha * p
        r = r - alpha * Ap
        r2_new = sum(r^2)
        err = sqrt(r2_new)

        if(verbose)
            cat(sprintf("Iteration %d, err = %.8f\n", i, err))

        if(err < eps)
            break
        beta = r2_new / r2
        p = r + beta * p
        r2 = r2_new
    }
    x
}

或许会有读者疑问，为什么我要把矩阵乘法定义成一个函数参数 Ax，而不是直接在算法过程中写矩阵乘法。这是因为，某些情况下矩阵乘法可能有特殊的实现，用户只需要定义好相应的函数，就可以直接调用上面的这段程序，而不需要去修改算法的细节。使用上面的程序，一个简单的模拟例子如下：

## Simulation example
set.seed(123)
n = 10000
p = 1000
x = matrix(rnorm(n * p), n)
b = rnorm(p)
y = x %*% b

beta_direct = solve(crossprod(x), crossprod(x, y))

mat_vec_mult = function(x, mat)
{
    as.numeric(crossprod(mat, mat %*% x))
}
xy = as.numeric(crossprod(x, y))
beta_cg = cg(mat_vec_mult, xy, mat = x)

max(abs(beta_direct - beta_cg))
## [1] 7.422063e-12

其中 CG 程序打印出了如下的信息：

Iteration 1, err = 80261.88521243
Iteration 2, err = 24276.83688338
...
Iteration 21, err = 0.00000622
Iteration 22, err = 0.00000197
Iteration 23, err = 0.00000062

可以看出，CG 在第 23 步迭代后就收敛了，在我的机器上耗时约 0.82 秒，而直接法总共耗时约 5.3 秒，是 CG 的将近 6.5 倍。

真有这么神奇？

看到这个结果，我估计小伙伴们都惊呆了。如果效果真这么好，那赶紧拿它去跑跑回归试试啊。于是我到 UCI 机器学习数据库上找了一个中等大小的数据集，包含 53500 个观测和 384 个自变量，然后兴冲冲地跑了个 CG（这里完全只是为了演示算法，实际处理数据时，请千万千万先对数据的背景有所了解，然后再考虑建模，切记切记）：

dat = read.csv("slice_localization_data.csv")
n = nrow(dat)
y = dat$reference
x = as.matrix(dat[, -c(1, ncol(dat))]) / sqrt(n)
xy = as.numeric(crossprod(x, y))

coeffs = cg(mat_vec_mult, xy, mat = x)
## Iteration 1, err = 11262.97730747
## Iteration 2, err = 4471.54099614
## Iteration 3, err = 1783.28640925
## ...
## Iteration 100, err = 2.94723420
## Iteration 101, err = 4.60232106
## Iteration 102, err = 4.02014578
## ...
## Iteration 200, err = 0.63018214
## Iteration 201, err = 1.67568741
## Iteration 202, err = 0.49243538
## ...
## Iteration 382, err = 0.16954617
## Iteration 383, err = 1.05050962
## Iteration 384, err = 0.11322079

纳尼？？怎么跟剧本写的不一样啊？说好的提前收敛呢？就算不提前不是说最多 m 步就收敛吗？我文章都写到这里了突然被打脸还怎么圆场啊？

（此处过去了半个小时……）

当崩塌的三观逐渐恢复的时候，就开始回过头来反思哪儿出了问题。其实，本文在之前有个非常重要的细节非常容易被忽视掉，大家把文章翻回第二节的第一句话，那里对矩阵 A 加了一个定语：正定。正定的代数意义表现在矩阵所有的特征值都大于 0，而在回归中，它等价于数据矩阵 X 是满秩的，换言之，没有多重共线性的存在。而如果我们检查一下这个数据中 X′X 的行列式，就会发现它等于 0，也就是说有多重共线性的存在——原来我们之前兴冲冲地犯了一个美丽的错误。

知道哪儿出错了就好办了，对于多重共线性，其中的一种应对办法就是给 X′X 的对角线上加上一个很小的常数 λ，这也就是我们常说的岭回归。我们重新修改一个岭回归版的矩阵运算函数，设定好 λ 参数和精度，再放到 CG 中去运行：

ridge = function(x, mat, lambda = 0.01)
{
    as.numeric(crossprod(mat, mat %*% x)) + lambda * x
}
coeffs_ridge = cg(ridge, xy, eps = 1e-3, mat = x, lambda = 0.01)
## Iteration 1, err = 11256.55983300
## Iteration 2, err = 4455.13459864
## Iteration 3, err = 1767.78523995
## ...
## Iteration 61, err = 0.00164239
## Iteration 62, err = 0.00127173
## Iteration 63, err = 0.00092021

这一回迭代 63 次就以 0.001 的精度收敛了，耗时约 4.2 秒。而更进一步，如果查看原始数据就会发现，这个数据的稀疏比例非常大，所以我们可以把矩阵转换成稀疏格式，再来尝试运行 CG：

library(Matrix)
xsp = as(x, "sparseMatrix")
coeffs_sparse_ridge = cg(ridge, xy, eps = 1e-3, mat = xsp, lambda = 0.01)

最后耗时约 2.6 秒。

前面那个错误使用 CG 的例子并不是我杜撰的，而是我在准备这篇文章的时候真实发生的事情。对于我自己而言也是一个教训：跑算法跑模型的时候，一定要仔细检查假定条件，然后对数据要有充分的了解，否则前方的终点就会跟非正定的 CG 一样，不收敛啊。

相信通过模拟和实际数据的例子，读者可以更直观地感受到 CG 的如下一些优点：

实现简单，会矩阵乘法就行，不会的话请会的人吃顿饭就够了；
内存占用小，妈妈再也不用担心花钱给我加内存了；
可以控制收敛精度，想到哪儿停就到哪儿停；
可以充分利用稀疏矩阵或者其他特殊的矩阵构造加快运算，激发小宇宙潜能。

本文的代码可以在 Github 上查看和下载。

参考文献：An Introduction to the Conjugate Gradient Method without the Agonizing Plain

普渡大学统计系博士，现为卡耐基梅隆大学博士后，感兴趣的方向包括计算统计学、机器学习、大型数据处理等，参与翻译了《应用预测建模》《R 语言编程艺术》《ggplot2：数据分析与图形艺术》等经典书籍，是 showtext、RSpectra、recosystem、prettydoc 等流行 R 软件包的作者。邱怡轩