False In-Sample Predictability?

摘要：Martin and Nagel (2019) 指出投资者 high-dimensional learning 有可能造成样本内虚假的可预测性。

01

让我们从两组实证结果说起。

下图是 Fama and French (2015) 五因子（除了 SMB）和 Carhart (1997) 动量因子在 1963 到 2008 年之间的表现，无一例外的，它们都获得了显著的超额收益。由于时间跨度和相关论文所涉及的实证区间接近，我们可以把它们视作样本内的表现。

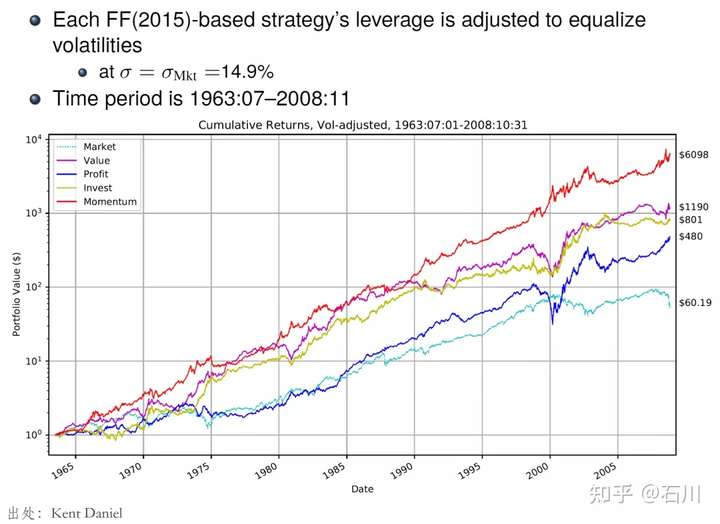
再来看看样本外……

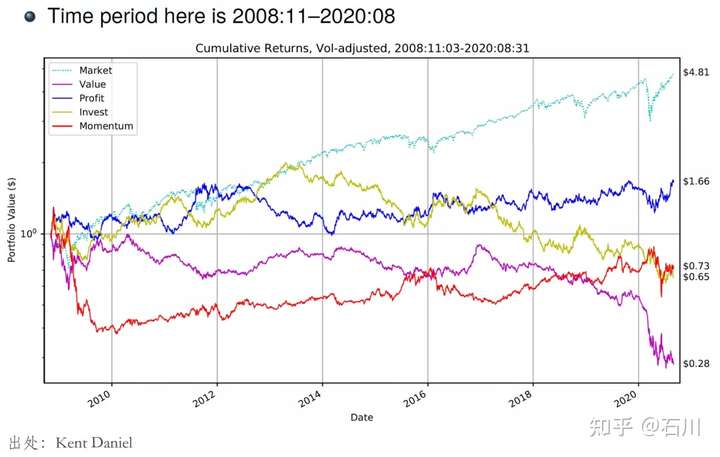
怎么说呢？“此时无声胜有声”。

看完了美股，再来看看 A 股上中国版四因子的表现。下图统计了市场、SMB、VMG（基于 Earnings-to-Price ratio 构造的价值因子）以及 PMO 四因子在样本内、外以及全样本的表现（样本的划分是根据该模型的论文）。

Again，“此时无声胜有声”。

此处无意进一步探讨因子的表现，只是想通过这两个例子引出本文要探讨的内容。在过去的 30 年，学术界提出了大量样本内显著的因子和异象（zoo of factors），然而绝大多数在样本外都无法持续。至于这背后的原因，目前有两种主流看法。一种是由于多重假设检验，大多数因子都是 p-hacking 的结果（Harvey, Liu, and Zhu (2016)）；另一种则是因子在样本外之所以变差是因为套利者把它们交易了（McLean and Pontiff (2016)）。

而今天要解读的 Martin and Nagel (2019) 则给出了第三种可能。该文题目是 Market Efficiency in the Age of Big Data，作者是 Ian Martin 和 Stefan Nagel。看过上期推文的小伙伴会知道这就是我说的 Stefan Nagel 的背靠背的第二篇。针对大量样本内显著样本外消失的可预测性，该文提出了一个新颖的视角 —— high-dimensional investor learning。

正如下图所描绘的，在大数据时代，人们面对着指数级增长的数据量，而能够影响公司未来基本面的变量也在无限扩张（例如会计报表数据，公司财报中的措辞，分析师一致预期，量价数据，公司所处行业的景气度，以及各种宏观经济变量和其他另类数据）。在这个背景下，传统的实证资产定价检验受到了巨大的挑战。

传统实证资产定价假设理性预期（rational expectation），即假设投资者知道哪些变量影响公司基本面以及它们和基本面的关系，即基本面预测变量 对投资者是已知的，并在这个前提下通过历史数据（在样本内）检验市场有效性。一旦原假设被拒绝便认为变量获得的超额收益代表着风险补偿或定价错误。

然而，Martin and Nagel (2019) 指出，在大数据时代，投资者根本无法知道到底哪些变量能够影响公司基本面，以及变量和基本面之间的关系 到底是什么样。取而代之的是在高维参数空间的学习问题，即估计 到底长什么样、参数是多少。在理性预期范式下，不存在投资者对 的学习问题，因此样本内检验发现的可预测性可以直接推广到样本外。然而，一旦投资者需要估计 且估计存在误差时，通过样本内检验发现的可预测性则无法再保证样本外的可预测性。

从直观上来理解，这是因为投资者高维学习问题会导致均衡状态下资产的价格和理性预期情况下相比出现偏差；该偏差的存在将造成事后（ex post）从计量经济学家的视角来看，已实现收益率不再随机，而是包含了一部分可预测的成分；因此当人们事后用统计检验分析变量和收益率的关系时，会误以为某些变量对收益率有预测性（且在高维问题下，即变量越来越多时，这个偏差造成的影响愈加明显）。

但实际的情况是，对投资者来说，这种可预测性在事前（ex ante）是感知不到的；对进行事后检验的计量经济学家来说，样本内的可预测性仅仅是源自由投资者学习 而导致的资产定价的偏差，因而是虚假的，这些变量在样本外并不能预测收益率。

因此，该文主张 high-dimensional investor learning 是诸多样本内 false discoveries 的另一个潜在原因，而唯有样本外的可预测性才真正代表风险补偿或错误定价。下图高度总结了该文。

下面就来深度解读这篇文章。

02 Model Setup

本节介绍 Martin and Nagel (2019) 使用的模型。

令 代表资产数，代表投资者用来预测资产未来现金流的变量（firm characteristics）的个数，令 （ 阶矩阵）表示 个公司的 个变量。不失一般性且为了简化推导，假设 。进一步假设代表资产的分红，而分红高低是投资者对资产估值的依据。模型假设 dividend growth 和 满足如下线性模型：

由上式可知，模型中假设 不随时间变化。在现实世界中，firm characteristics 当然会随时间发生变化，且 dividend growth 也完全有可能是 的非线性函数，但是允许 时变或考虑非线性将会使得研究 learning 问题的难度陡然增加（就现在这个简单的设定而言，问题本身已经十分复杂）。由于 Martin and Nagel (2019) 是第一篇通过建模研究 investor learning 对 asset pricing 和 return predictability 影响的文章，因此他们决定尽量简化模型[1]。

在模型中，参数向量 决定了变量如何影响资产未来 dividend growth 的变化，而它也正是投资者在高维变量空间中需要估计的（learning）。模型假设 满足多元正态分布：

其中 是一个常数，是 阶单位矩阵。这个假设的核心是 的方差和 （变量的个数）成反比。它对模型尽可能贴合现实世界至关重要。这是因为上述假设保证了无论 怎么变，模型中的信噪比都是不变的。如果没有这个约束，则随着使用的变量越来越多，中可解释的部分将会越来越大，远超过噪音 ，这显然是不切实际的。以上就是关于资产基本面的建模。

接下来是关于投资者的设定。该文假设投资者是风险中性（risk-neutral）以及同质的（homogeneous）。此外，他们还假设无风险收益率为 0。在风险中性 + 无风险收益率为 0 下，资产的 risk premium 为零，因此稍后对模型求解时发现的任何 in-sample return predictability 都不应归结为 risk premium（因为 risk premium 已经在模型中被排除了）。同质性则意味着所有投资者对于 的估计是一样的，不会因人而异，且投资者之间不会相互学习。

有了资产和投资者，接下来就要开始研究投资者如何对资产估值、确定其均衡状态下的价格，以及在这个过程中造成的资产收益率的可预测性。为了简化，Martin and Nagel (2019) 使用了单期估值模型。由于投资者是风险中性且利率为零，因此 期资产的价格等于 期分红在 时刻的期望：

由上式可知，均衡状态下资产的价格 取决于投资者如何形成 的预期，即由投资者如何形成关于 的预期决定。而由于 ，因此 最终和投资者如何在高维变量空间估计 密切相关。从计量经济学家事后检验的角度出发，投资者在高维空间下对 的（不准确）估计如何影响资产的价格，以及这种影响是否能够造成任何样本内（虚假的）可预测性呢？这就是 Martin and Nagel (2019) 想要回答的问题。

03 Rational Expectation

在探讨 investor learning 之前，我们先来看基准，即理性预期的情况。

理性预期下假设投资者知道真实的 （即无需估计），因此有 ，以及。利用下期 和理性预期下的资产价格 ，就可以计算出realized price change，即收益率（Martin and Nagel (2019) 将 realized price change 称作“收益率”，本文遵循这一术语使用）：

在理性预期下，由于投资者无需估计 ，因而有 。这意味着哪怕是事后检验来看，样本内也没有任何可预测性。为说明这一点，假设事后使用 对 进行截面回归，得到回归系数向量：

由于 ，将其代入有：

从实证资产定价检验的角度来说，我们关注的是事后联合检验 是否显著偏离零 —— 显著偏离零意味着有（样本内）的可预测性。利用统计检验，满足 分布，因此只要利用实际的样本数据就可以对其检验。由 的定义可知，在理性预期下，任何偏离零都是由于噪音 造成的。

除了直接联合检验 ，我们也可以从另一个角度理解。令 ，并考虑以 为权重构造的投资组合（这对应了常用的样本内构造投资组合并检验其收益率）。该投资组合的收益率为：

由 满足 分布可知，该投资组合的预期收益为：

在没有任何可预测性的原假设下，该投资组合在样本内的预期收益为 ，它之所以大于零仅是因为对样本内噪音的过拟合。在事后检验中，常规操作就是考察该投资组合的收益率是否显著的偏离 。如果发现显著的偏离，人们会认为 可以预测 ，并把可预测性归结于风险补偿或投资者的系统性偏误。然而，若投资者不知道真实的 ，而是需要对它估计（learning）时又会怎样呢？估计的不准确是否会造成上述原假设被错误地拒绝呢（即样本内虚假的可预测性）？

04 OLS Learning

首先来看最简单（但稍微不太满足实际）的情况 —— 投资者直接使用 OLS 来估计 ，即 OLS learning。至于为什么说它稍微不满足现实，我们放到第 5 节介绍 Bayesian Learning 时讨论。

为估计 ，假设投资者首先计算全部 期 dividend growths 的均值：

然后用 对 回归有：

和理性预期（上一节）不同，由于投资者不知道真实的 ，而是通过 OLS 估计，因此这将影响他们对资产未来 dividend growth 的估计 。在这个情况下，均衡状态下资产的价格为：

而 realized return 为：

站在投资者在 时刻的视角，他们是无法察觉对的估计有偏误的，因此对于投资者来说， 依然是不可预测的，正如理性预期一样。然而，对于事后进行统计检验来说，上述通过 OLS 估计的 是否影响检验结果呢？

定义 ，因而有 。将该式代入 的表达式并进行简单代数运算有：

将其代入 的表达式可得：

怎么样，在 OLS learning 下， 看着和理性预期下不一样了。下表对它们进行了对比：

和理性预期相比，投资者对 的 OLS 估计造成 realized return 中多出了一项，即 。因此，当我们如常进行事后统计检验时，收益率对 的回归系数 就变成了：

与理性预期相比，OLS learning 造成事后检验的回归系数 中也多了一项（上式中第一项）。观察该项，从直觉上可知，如果 中的某些 firm characteristics 和误差 正相关或者负相关时，就很有可能造成 联合起来显著偏离零且原假设被（错误地）拒绝。

如果我们仍然从投资组合收益率的视角来解读，那么在 OLS learning 下，可以推导出该投资组合的预期收益中同样包含两项，较理性预期的情况下多了一项：

没有可预测性的原假设下， 的预期是 （理性预期的情况）。然而，由于 OLS learning 造成了额外的一项 。当 很小，或者 （用来预测 dividend growth 的变量的个数）非常大的时候（即 high-dimensional learning 问题）， 这一项将会造成 相对 的显著偏离，使得事后统计检验拒绝原假设，认为 中有某些变量能够预测 [2]。

让我们串一下上面“可预测性”产生的逻辑。该逻辑是因为投资者不知道 ，而是通过 OLS 来估计 ，并根据 对资产估值，产生均衡状态下资产的价格。它进而造成了和理性预期相比，已实现收益率中出现额外一项，而这个额外项继而造成了回归系数 显著地联合偏离零或投资组合预期收益显著的偏离 ，让人们（错误地）拒绝原假设。由于在模型中已经排除了 risk premium，因此该样本内的可预测性仅仅是 investor learning 造成的。

05 Bayesian Learning

通过上一节的介绍，希望各位小伙伴搞清楚 Martin and Nagel (2019) 想要干什么了。但是我负责的说，OLS learning 因为有些问题，并不是他们关注的重点。下面就来上点“硬货”—— Bayesian learning。

好消息是，有了 OLS learning 做铺垫，本节的内容会容易理解地多（我写起来也容易的多）。

为了简化模型，Martin and Nagel (2019) 假设投资者的先验是 的真实分布，即 。经过推导，可以得到投资者对 的后验估计：

和 OLS learning 相比，Bayesian learning 下的 是先验和 OLS 估计之间的贝叶斯收缩。为了更直观的理解往先验的收缩，上述 又可以写作：

其中 是收缩系数，而往先验收缩的程度满足如下性质（都非常复合直觉）：

1. 越小，越往先验收缩（样本点的时间跨度越短，误差越大）；

2. 越小，越往先验收缩（ 决定了先验中 相对零的偏离程度）；

3. 越大，越往先验收缩（变量个数越多，越有可能对着样本内过拟合，因此更需要压缩）。

比较 Bayesian learning 和 OLS learning 可知二者的差异就体现在 上。数学运算可知，当先验是扩散的时候（ ），收敛到单位矩阵。因此，OLS learning 是 Bayesian learning 的一个特例。现在我们就可以回答前面遗留的问题：为什么 OLS learning 不太合理。由 的定义可知，变量偏离零的程度由 确定。如果 非常大，则意味着 dividend growth 的信噪比非常高（有很大一部分可以通过 来预测），这显然与真实世界不符。由于在真实世界中投资者通常不会认为 dividend growth 中有很大一部分能够被预测，因此 Bayesian learning 比 OLS learning 更符合实际。

在 Bayesian learning 下，投资者通过 来判断 dividend growth 并对资产估值。在均衡状态下，收益率满足：

毫无疑问，和理性预期以及 OLS learning 相比，这个 看着更复杂了。不用慌，我们再放在一起对比一下：

在上表中，我特地使用了相同的颜色圈出了相似的项。和 OLS learning 相比，Bayesian learning 中又多了额外的一项（第一项），而它的第二项则对应 OLS learning 的第一项，其中的差异是，Bayesian Learning 的第二项中多了收缩系数 。Bayesian learning 下 中的三项可以解读为：

1. 第一项是因为往先验收缩，因此投资者对基本面信息 的“反应不足”（如果不收缩，即 ，这一项就会消失）。

2. 第二项和 OLS learning 类似，是噪声对投资者估计的影响。不过 的存在意味着先验使得投资者对噪音的反应没那么强烈，因此从一定程度上降低了这部分对估计的影响；在 Bayesian learning 下， 在前两项误差之间实现了最优的权衡。

3. 最后一项和理性预期一样，为 。

接下来如法炮制，利用上述 来估计并检验 ，以及检验利用它构造的投资组合的预期收益。和 一样，由于 Bayesian learning， 也有三项，分别对应 的三项（不再赘述）。而该投资组合的预期收益为：

当 时，上式收敛到 OLS learning 的情况，即 。下图给出了 OLS learning 和 Bayesian learning（informative prior）两种情况下，该投资组合预期收益如何随 的增加而变化。当没有先验时，OLS learning 更容易过拟合，因此其预期收益随 升高的更快。使用贝叶斯收缩之后，会从一定程度上减弱这个情况，但却无法从根本上消除样本内的可预测性。

最后，我们再来回顾下“可预测性”产生的原因。投资者通过 Bayesian learning 估计并根据对资产估值，产生均衡状态下资产的价格。这造成了和理性预期相比，已实现收益率中的额外的两项，而这两项进而造成利用 构造的投资组合的预期收益显著的偏离 ，让人们（错误地）拒绝原假设。因此，该样本内的可预测性仅仅是 investor learning 造成的。

哪怕是采用了更加接近现实的 Bayesian learning，投资者的 high-dimensional learning 依然会产生样本内虚假的可预测性。

06 Out-Of-Sample

以上就是关于投资者的 high-dimensional learning 如何影响事后样本内统计检验的研究。在该文的后半部分，Martin and Nagel (2019) 也详细讨论了样本外的可预测性。结论就是，investor learning 不会产生样本外的可预测性，这显然非常符合逻辑。按照投资组合的视角，它可以表述为：

假设有两个互不重叠的时间窗口。如果我们使用窗口 1 来检验 并发现了一些虚假的可预测性，则使用它们作为系数的投资组合在窗口 2 内的预期收益为零；唯有当窗口 1 内发现的可预测性是真实的（即不是由 investor learning 造成的虚假的可预测性），通过它们才能在窗口 2 内（样本外）获得显著大于零的超额收益。

就我个人的看法，Martin and Nagel (2019) 的发现对学术界的意义重大。在实证资产定价研究中，学术界通常假设理性预期（即投资者不存在学习问题），因而无一例外都是事后通过样本内的数据来检验某个异象或者因子的超额收益是否显著大于零。这一惯例在过去 30 年内产生了大量样本内显著的异象，但是其中的绝大多数在样本外压根不好使或者无法被复现（Hou, Xue, and Zhang (2020)）。而究其原因，除了 p-hacking 以及被套利走之外，Martin and Nagel (2019) 给出了另一个解释。

在大数据时代，我们有了过去无可比拟的数据量。然而，投资者面临更加复杂的高维预测和估计问题。大数据如何影响投资者的估计，如何影响均衡状态下资产的价格，如何影响市场的有效性？这些都是等待回答的问题。毫无疑问，Martin and Nagel (2019) 是一个有益和大胆的尝试，而它提出的 investor learning 问题也足以引起人们的重视。

所有历史数据都是样本内[3]。

备注：

1. 但这丝毫不影响这是一个很好的开端，我们也有理由期待今后拓展的模型会有更深入的发现。
2. 如果很小，则 即使造成了偏离也并不大，因此这一项在 high-dimensional learning 中才格外重要。
3. 见《所有历史数据都是样本内》。

参考文献

• Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.
• Fama, E. F. and K. R. French (2015). A five-factor asset pricing model.Journal of Financial Economics 116(1), 1 – 22.
• Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5 – 68.
• Hou, K., C. Xue, and L. Zhang (2020). Replicating anomalies. Review of Financial Studies 33(5), 2019 – 2133.
• McLean, R. D. and J. Pontiff (2016). Does academic research destroy stock return predictability? Journal of Finance 71(1), 5 – 32.
• Martin, I. and S. Nagel (2019). Market efficiency in the age of big data. Working paper, available at: https://ssrn.com/abstract=3511296.

免责声明：入市有风险，投资需谨慎。在任何情况下，本文的内容、信息及数据或所表述的意见并不构成对任何人的投资建议。在任何情况下，本文作者及所属机构不对任何人因使用本文的任何内容所引致的任何损失负任何责任。除特别说明外，文中图表均直接或间接来自于相应论文，仅为介绍之用，版权归原作者和期刊所有。

原创不易，请保护版权。如需转载，请联系获得授权，并注明出处。已委托“维权骑士”(维权骑士-版权保护 版权知识 原创检测 识别字体 著作权登记) 为进行维权行动。