【Complex Analysis3】共形映射

基本定义

w=f(z)把曲线C映射到曲线Γ,z0∈C,w0∈Γ,w0=f(z0)
把邻域映射到邻域z=z0+∣Δz∣eiθ,w=w0+∣Δw∣eiϕ
如果limz→z0∣w−w0∣∣z−z0∣存在，那么这个极限值叫做曲线C经函数w=f(z)映射后在z0处的 伸缩率
如果limz→z0(ϕ−θ)存在，那么这个极限值叫做曲线C经函数w=f(z)映射后在z0处的 旋转角

（保角性（conformal） 也可以这么理解：任意过z0的两条曲线有一个夹角，曲线经过f映射后的两条曲线也有一个夹角。对于任意两条曲线，f映射前后的这两个夹角都相等。）

（TH：if f is analytic and f′(z0)≠0 then f is conformal at z0）
如果w=f(z)在D内解析，那么f′(z0)=limΔz→0ΔwΔz=limΔz→0∣Δw∣∣Δz∣ei(ϕ−θ)
limΔz→0∣Δw∣∣Δz∣=∣f′(z0)∣，也就是说，对于任何过z0的曲线C，伸缩率都不变，这种性质叫做 伸缩率不变性
limΔz→0(ϕ−θ)=argf′(z0)，也就是说，对于任何过z0的曲线C，旋转角都不变，这种性质叫做 旋转角不变性
（f′(z0)≠0是必要的，否则保角性将不成立）

共形映射

对于D内的映射w=f(z),如果它在任一点都具有 伸缩率不变性 和 旋转角不变性 称w=f(z)是 第一类保角映射
如果伸缩率不变，保持角度不变但方向相反，称为 第二类保角映射
（根据上一部分的分析，如果w=f(z)在D内解析，那么一定在D内是保角映射）

共形映射 w=f(z)是区域D内的 第一类保角映射，并且当z1≠z2，有f(z1)≠f(z2)

Möbius transformations

Möbius transformations（分式线性映射）定义为这样的映射： w=az+bcz+d,(ad−bc≠0)
性质（定义ˆC=C∪{∞}）：

• 在ˆC上是一一映射
• 是ˆC→ˆC的包角映射，也是唯一的满足ˆC→ˆC的包角映射
  （保角性很好证明，解析、非0 必保角）
• 保圆性，也就是把圆映射到圆（把直线看成无限大的圆）
• Given three distinct points z1,z2,z3∈ˆC, there exists a unique Möbius transformation f such that f(z1)=0,f(z2)=1,f(z3)=∞.

分式线性映射可以分解成以下4种简单函数

1. w=z+b（b是复数），是平移映射（translation）
2. w=zeiθ,(θ∈R),是旋转映射（rotation）
3. w=rz,(r>0,r∈R),是相似映射（把曲线放大）（dilation）
4. w=1z,是反演映射，（可以理解关于单位圆做一个对称）（inversion）

（为了形象理解反演映射，写了个动画程序,可以自行运行试试看）

# 复变函数1/z的可视化动画
import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(5, 5))
ax = fig.subplots(1, 1)

line1, line2 = ax.plot(0, 0, 'bo'), ax.plot(0, 0, 'ro')

circle = np.exp(1j * 2 * np.pi * np.linspace(0, 1, 100))
line3 = ax.plot(circle.real, circle.imag)

ax.set_xlim(-1, 5)
ax.set_ylim(-1, 5)
plt.ion()  # 第一个重要的点
p = plt.show()  # 第二个重要的点

for r in np.linspace(0.2,5,200):
    z = r * np.exp(np.linspace(0, 1, 10) * 2 * np.pi * 1j)
    w = 1 / z
    plt.setp(line1, 'xdata', z.real, 'ydata', z.imag)  # 第三个重要的点
    plt.setp(line2, 'xdata', w.real, 'ydata', w.imag)  # 第三个重要的点
    plt.pause(0.1)  # 第四个重要的点

TH1 分式线性映射是共形映射

Möbius transformations 的保圆性

TH2 Möbius transformations 有保圆性。
所谓保圆性，是把圆映射到圆。（可以把直线也看成是无穷大的圆）

证明：（假设∣z−O∣=r,w=f(z)）

• 对于前三种映射，可以这样证明保角性 w=az+b⟹z=(w−b)/a⟹∣(w−b)/a−O∣=r
• 对于inversion，用同样的方法可以证明保圆性

直观理解如下：

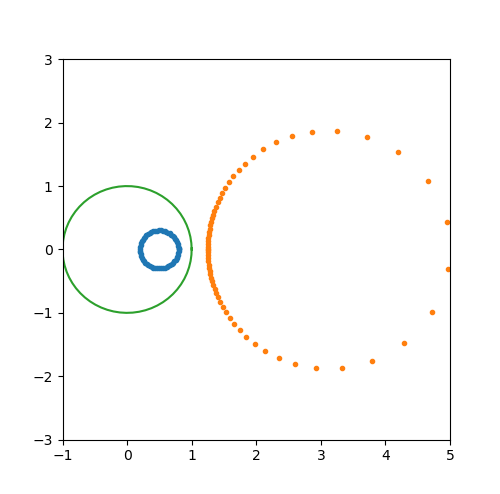
# 保圆性的可视化
import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(5, 5))
ax = fig.subplots(1, 1)
unit_circle = np.exp(1j * np.linspace(0, 2 * np.pi, 30))
z = 1 + 1j + unit_circle * 0.5
w = 1 / z

line1 = ax.plot(z.real, z.imag, '.r')
line2 = ax.plot(w.real, w.imag, '.b')
line3 = ax.plot(unit_circle.real, unit_circle.imag)
plt.show()

Möbius transformations 的性质3

TH3 Given three distinct points z1,z2,z3∈ˆC, there exists a unique Möbius transformation f such that f(z1)=0,f(z2)=1,f(z3)=∞.

In fact,
f(z)=z−z1z−z3z2−z3z2−z1

其它性质

• TH4 The composition of two Möbius transformations is a Möbius transformation, and so is the inverse.
• TH5 Given three distinct points z1,z2,z3 and three distinct points w1,w2,w3, there exists a unique Möbius transformation f:ˆC→ˆC that maps zj to wj, j = 1, 2, 3. （用TH3和TH4可证明）

The Riemann Mapping Theorem

wiki, coursera

If D is a simply connected domain (= open, connected, no holes) in the complex plane, but not the entire complex plane, then there is a conformal map ( = analytic, one-to-one, onto) of D onto the open unit disk D.

参考资料

coursera:Introduction to Complex Analysis
李红：《复变函数与积分变换》高等教育出版社
“十五”国家规划教材《复变函数与积分变换》高等教育出版社
钟玉泉：《复变函数论》高等教育出版社