动态规划算法有什么用？使用C语言编程解决一个实际问题，通俗易懂的学习动态规划法

上一节讨论了程序开发中常用的分治算法，我们总结出使用该算法的其中一条“适用条件”为：原始问题可以拆分为**彼此独立**的子问题。这个条件其实不是使用“分治算法”的必要条件，只不过若子问题有重叠，分治算法会做许多不必要的重复工作，它会反复的求解那些公共的重叠子子问题。因此，如果子问题有重叠，一般不再推荐使用分治算法，可以考虑动态规划。

动态规划的基本思想

动态规划与分治算法相似，都是通过组合子问题的解来获得原始问题的解。只不过与分治算法不同，动态规划特别适合应用于子问题重叠的情况，它对每个子子问题只求解一次，并将解保存，之后求解其他依赖该子子问题的问题时，只需要从保存的结果中找出对应的解即可，这样就避免了反复求解公共的重叠子问题。

由此可以看出，动态规划算法本质上是牺牲部分空间换取时间效率。

钢条切割问题

上面的内容有些枯燥，来看一个实际问题：某公司的主营业务是购买长钢条，将其切割成短钢条出售。已知切割工序本身的成本可以忽略不计，不同长度单位的钢条价格如下表：

假设有一段长度为 n 的钢条，问怎样切割才能获得最大的收益？

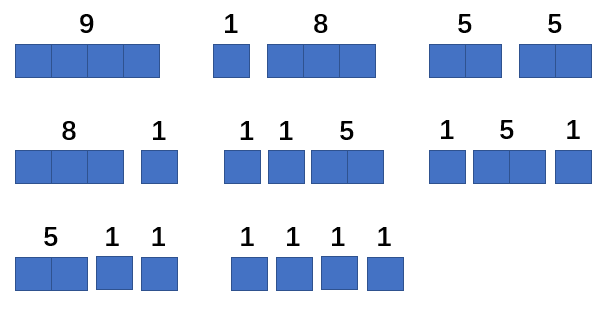
从钢条价格表可以看出，切割方案都是整数单位切割，对于长度为 n 的钢条，每个单位位置处都有 2 种可能（切，不切），因此总共有 2n-1 种切割方案，以 n=4 为例，共有以下 8 种切割方案：

8 种切割方案

容易看出，把长为 4 的钢条切割成 2 个长为 2 的钢条时，能够获得最大的收益为 5+5=10。

暴力穷举法

暴力穷举法的确能够解决问题，但是却不一定能够获得满意的效率。前面提到，对于长度为 n 的钢条有 2n-1 种切割方案，当 n 足够大时，“指数爆炸效应”很容易让这种解决方案难以在可接受时间内给出结果。

令最优解为收益最大，为了便于讨论，我们使用加法符号“+”表示切割方案，例如 4 = 2+1+1 表示将长度为 4 的钢条切割为三段长分别为 2、1、1的短钢条。因此对于长度为 n 的钢条，假设一个最优解是将钢条切割为 k 段，那么对应的切割方案为：

n = i1 + i2 +...+ ik

最优切割方案确定后，最大的收益也就确定了——直接查表即可，设长度为 n 的钢条对应的最大收益为 mpn，则：

mpn = pi1 + pi2 +...+ pik

一个容易想到的解决方法是：从钢条左边切割下长度为 i 的一段，右边余下的钢条长度为 n-i，左边的钢条不再分割，只对右边的钢条递归继续分割。然后我们让 i 从 1 遍历到 n，也就遍历了所有的分割方案，遍历过程中，保存最大收益，即可得到解，使用数学公式描述这一过程，也即：

mpn = max(pi + mpn-i)，其中 1≤i≤n

现在我们使用C语言编写程序来实现上述算法，使用递归是方便的：

int p[N] = {0,1,5,8,9,10,17,17,20,24,30...
int max_price(int n)
{
    if (0==n)
        return 0;

    int mp = -1, i;
    for (i=1; i<=n; i++) {
        mp = max(mp, p[i]+max_price(n-i));
    }
    return mp;
}

如果读者读过我之前的文章，就应该明白对于C语言中的递归函数，我们更应该从实际需求角度分析它。max_price() 函数接收整数 n，返回长度为 n 的钢条的最大收益。若 n=0，不可能有任何收益，所以直接返回 0。接着，我们定义了变量 mp 用于存放最大收益，因为接下来要取它和分割方案对应的收益（大于0），所以给 mp 赋了负值作为初值。接下来的 for() 循环其实就是在描述公式 mpn = max(pi + mpn-i)。

读者可自行编写 main() 函数测试 max_price()，会发现 max_price(n) 函数的确能够正确计算长度为 n 的钢条最大收益值，例如 max_price(4)=10，max_price(10)=30。

不过解决问题倒不难，难点在于要“有效率”的解决问题，读者可自行测试，随着输入给 max_price() 的参数值逐渐增大，函数执行消耗时间急剧增加。在我的电脑上，max_price(16) 消耗 112ms 的时间，max_price(17) 消耗 332ms 的时间，每将 n 提升 1，函数执行时间就翻一倍多，当 n=30 时，我甚至没有耐心等下去了（我等了10多分钟，函数还没有执行完成）。

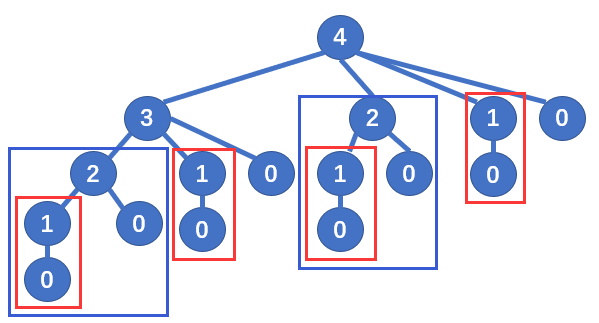
可见，暴力穷举法容易想到，也容易实现，但是却往往不能带来足够令人满意的效率。仔细考虑一下，应该不难发现，暴力穷举法的效率之所以如此低下，主要是因为中间产生了很多不必要的重复计算。请看下图：

有很多重复计算

以 n=4 规模的求解为例，n=2 规模（蓝框）的求解会被更大规模（n=3、4）的求解重复计算，同理，n=1 规模（红框）的求解则会重复更多次。当 n 更大时，这些重复计算会越来越多，不难证明，随着 n 的增加，max_price() 函数的工作量会指数爆炸式的增长。

动态规划法

前文分析到，暴力穷举法之所以效率低下，根本原因在于执行了许多不必要的重复计算，如果能够避免这些重复计算，那么算法的效率必定会得到大大的提升。一个容易想到的方法是每计算一个子问题，就把该子问题的解存储起来，下次需要求解该子问题时，直接查询即可，从而避免重复计算。这其实就是动态规划法的基本思想。

时间效率对比

为了有更直观的感受，下面将对比本文实现的三种算法的时间效率，读者应该将注意力放在算法消耗时间的相对值上，绝对值在不同机器上是没有意义的。

三种算法的时间效率差异已经一目了然了我使用的计量单位最小为 1ms，在 n 等于 30 时，暴力穷举法的时间超过 2 分钟是因为我等待了两分钟还没有结果，我没有耐心，提前结束它了，实际的时间应该远大于 2 分钟。

另外，动态规划法 1 由于使用了递归处理，所以当 n 很大时，将消耗完堆栈空间，导致程序出现段错误。

无论是上一节介绍的分治算法，还是本节讨论的动态规划算法，都是再程序开发中设计高效算法的基础。其实稍稍思考一下，应该不难发现，我们在获得时间高效率的时，通常都是要付出消耗更多空间的代价的，“天下没有免费的午餐”，这样的思想其实也可以应用于程序开发中。在之后的学习中，我们将对此观点的认识更加清晰。

max_price() 函数仅给出了最大的收益，如何添加代码输出对应的分割方案，留个读者自己考虑了。