计算机图形学基础（2）——变换

上一篇文章我们介绍了计算机图形学中的线性代数基础，包括：点、向量、矩阵等。本文，我们将介绍向量和矩阵的进一步应用——变换。

计算机图形学中，我们可能会对图形进行各种变换（Transform），如：

• 缩放（Scale）
• 平移（Transation）
• 旋转（Rotation）
• 切变（Shear）

首先，我们来介绍一下 2D 变换，以便了解变换是如何通过矩阵变换来实现的。

对于缩放变换，它主要包含两种：等比例缩放、非等比缩放。

等比例缩放

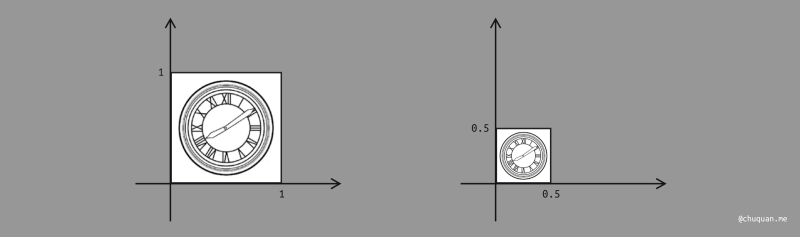
上图所示，为等比例缩放的示意图。根据等比例缩放的规则，我们可以根据缩放前 x 和 y 的值，得到一组关系式，如下所示。

x′=sxy′=sy

根据此关系式，我们可以进一步推导出缩放矩阵及关系式，如下所示。

(x′y′)=(s00s)(xy)

非等比缩放

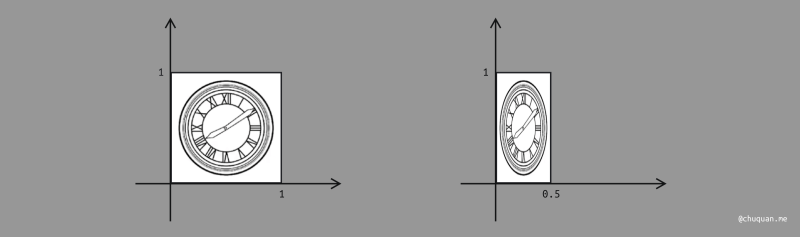
上图所示，为非等比缩放的示意图。根据非比缩放的规则，我们可以根据缩放前 x 和 y 的值，得到另一组关系式，如下所示。

x′=sxxy′=syy

根据此关系式，我们可以进一步推导出缩放矩阵及关系式，如下所示。对比一下，非等比缩放与等比例缩放的关系式非常相似。

(x′y′)=(sx00sy)(xy)

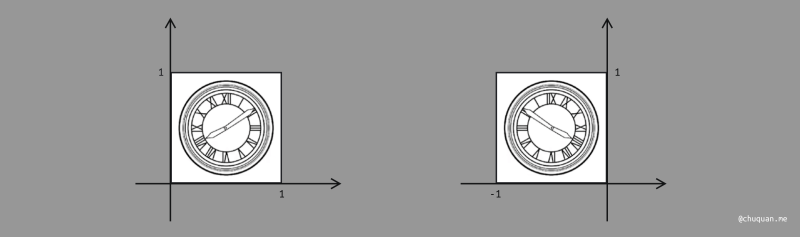
上图所示，为镜像变换的示意图。我们可以根据原始的 x 和 y 的值，得到一组关系式，如下所示。

x′=−xy′=y

根据此关系式，我们可以进一步推导出镜像矩阵及关系式，如下所示。本质上，镜像变换是一种特殊的缩放变换。

(x′y′)=(−1001)(xy)

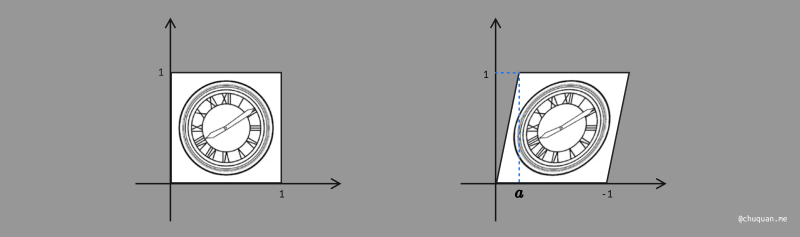
上图所示，为切变变换的示意图。切变变换相对复杂一点，其 y 坐标值与 x 坐标值成一个比例关系。不过，我们仍然可以根据原始的 x 和 y 的值，得到一组关系式，如下所示。

x′=x+ayy′=y

根据此关系式，我们可以进一步推导出镜像矩阵及关系式，如下所示。本质上，镜像变换是一种特殊的缩放变换。

(x′y′)=(1a01)(xy)

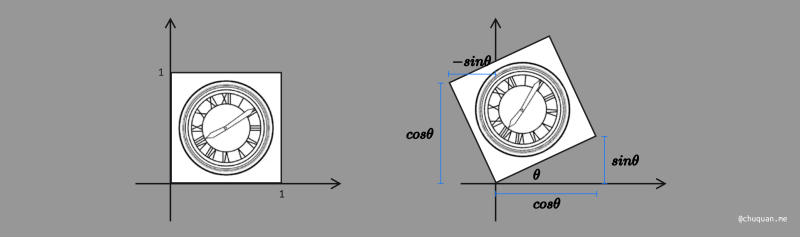
上图所示，为旋转变换的示意图。旋转变换的坐标推导需要借助三角函数，最终可得到如下一组关系式。

x′=cosθx−sinθyy′=sinθx+cosθy

根据此关系式，我们可以进一步推导出旋转矩阵及关系式，如下所示。

(x′y′)=(cosθ−sinθsinθcosθ)(xy)

截止目前位置，所有的的变换都可以通过推导得出一个变换矩阵，以此矩阵乘以任意点（以矩阵表示），都可以得到转换后的点（以矩阵表示），符合线性变换。

下面，我们来看一下比较特殊的平移变换。

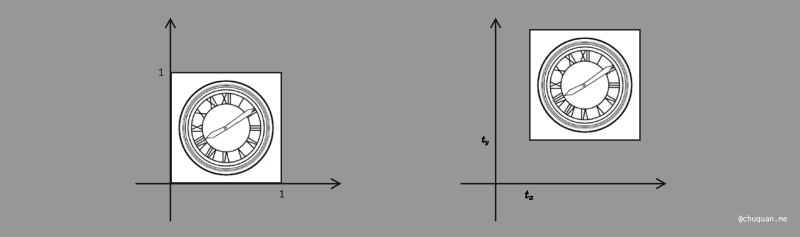
上图所示，为平移变换的示意图，同样，我们也可以可得到如下一组关系式。

x′=x+txy′=y+ty

但是，我们进一步推导，得到的关系式与之前的变换不同，它有额外的偏移量，不符合线性变换，如下所示。

(x′y′)=(1001)(xy)+(txty)

我们总是希望能使用一个统一的关系式来描述各种变换，然而，平移变换打破了我们的美好预期。那么该如何解决呢？为此，我们引入了齐次坐标。

为了能够统一表示所有变换，我们引入了 齐次坐标（Homogenous Coordinates）。这里的核心思想是为每一个点或向量添加一个额外的 w 坐标。

点的齐次坐标表示：向量的齐次坐标表示：2D点的齐次坐标表示：(xy1)2D向量的齐次坐标表示：(xy0)

此时，我们再来尝试推导平移变换矩阵以及其关系式，可以得到如下所示内容。很显然，原来关系式中的偏移量没有了。

(x′y′w′)=(10tx01ty001)(xy1)=(x+txy+ty1)

仿射变换与线性变换

我们将线性变换和平移变换的组合，称为 仿射变换（Affine Transform），如下所示。在未引入齐次坐标之前，我们推导出来的平移变换就是一种仿射变换。

(x′y′)=(abcd)(xy)+(txty)

当引入齐次坐标之后，所有的变换都可以统一使用线性变换来表示，如下所示。

(x′y′1)=(abtxcdty001)(xy1)

如下所示，是引入齐次坐标后，缩放变换，旋转变换，平移变换所对应的变换矩阵。

缩放变换：旋转变换：平移变换：缩放变换：S(sx,sy)=(sx000sy0001)旋转变换：R(α)=(cosα−sinα0sinαcosα0001)平移变换：T(tx,ty)=(10tx01ty001)

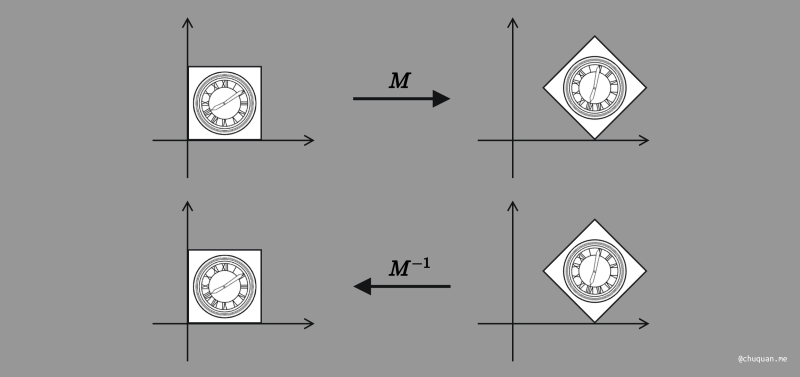
我们将所有的反向变换都称为 逆变换（Inverse Transform），比如：我们将从 A 平移到 B 称为平移变换，那么从 B 平移到 A 则可称为逆变换，其他的缩放变换、旋转变换同样如此。

上一节，我们引入了齐次坐标后，所有的变换都可以转换成线性变换，其中以 M 为变换矩阵。而这些变换的逆变换，同样可以使用线性变换来表示，并以 M 的逆矩阵 M−1 为变换矩阵。

在真实情况下，我们遇到的变换大多数都是组合变换，也就是同时包含了缩放、旋转、平移等多种变换。

多种变换组合时，变换的顺序其实是非常重要的，我们以如下一个例子来进行介绍。

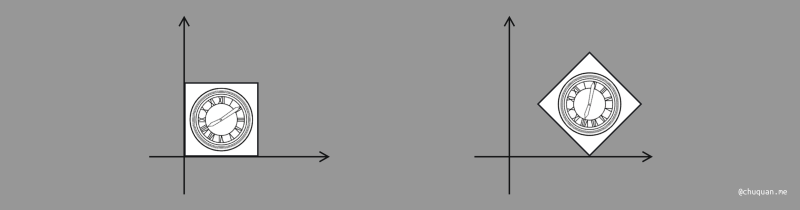
对于上面这种变换，如果我们先平移，再旋转，那么最终会变成如下所示的。这里的根本原因在于旋转变换时，仍然是以坐标原点为锚点进行旋转。

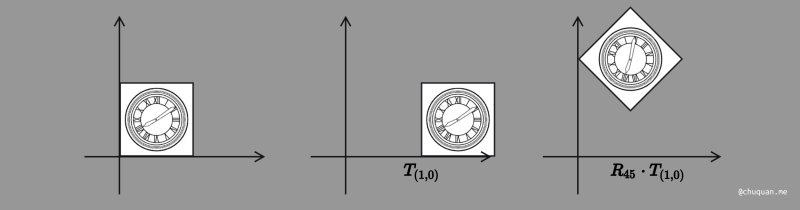
对此，正确的顺序应该是先旋转，后平移，这样才能达到预期的效果。

不同的顺序，矩阵变换的结果完全不同。前一篇文章我们提到过矩阵乘法不符合交换律，从这一点其实也能够解释这个现象。

在实际开发中，遇到这种类似的情况，我们一般都会先将目标平移至原点，然后进行各种其他变换，然后再通过逆变换平移回去。

关于 3D 变换，本质上与 2D 变换一样，只不多在矩阵表示上多了一个维度而已。

当我们引入齐次坐标之后，3D 的点和向量可以采用如下方式表示。

点的齐次坐标表示：向量的齐次坐标表示：3D点的齐次坐标表示：(xyz1)3D向量的齐次坐标表示：(xyz0)

与此对应，3D 变换的矩阵变换关系式为如下所示。

(x′y′z′1)=(abctxdeftyghitz0001)(xyz1)

如下所示，为 3D 空间中的缩放变换的变换矩阵的定义。

S(sx,sy,sz)=(sx0000sy0000sz00001)

如下所示，为 3D 空间中的平移变换的变换矩阵的定义。

T(tx,ty,tz)=(100tx010ty001tz0001)

如下所示，为 3D 空间中的旋转变换的变换矩阵的定义，沿着不同的轴旋转，变换矩阵的定义也有所不同。

Rx(α)=(10000cosα−sinα00sinαcosα00001)Ry(α)=(cosα0sinα00100−sinα0cosα00001)Rz(α)=(cosα−sinα00sinαcosα0000100001)

本文我们简单梳理了一下缩放、旋转、平移几种变换对应的矩阵关系式。其中，平移变换比较特殊，为了能够统一关系式，我们引入了齐次坐标，在点、向量的矩阵表示中增加了一个维度。然后，我们介绍了一下在组合变换中变换顺序的重要性。最后，我们简单总结了 3D 变换的矩阵关系式。

1. 《GAMES 101》
2. 《计算机图形学入门：3D渲染指南》