Новое доказательство того, что P≠NP: окончательное обновление - почти наверняка...

Доказательств того, что P=NP, и даже для менее интересного и более вероятного P≠NP, очень много. Большинство из них принадлежит энтузиастам, которых, как правило, можно похвалить за энтузиазм, но не за доказательства. Однако последнее доказательство принадлежит уважаемому теоретику сложности и не может быть отвергнуто обычным способом.

Последнее обновление: статья отозвана.

Финальное обновление 1 сентября.

Вероятно, это будет последнее обновление, поскольку, если не считать теоретиков сложности, которым интересно знать подробности, вопрос, по сути, решен.

30 августа статья была удалена из ArXiv ее автором, профессором Блюмом, и добавлено пояснение:

Комментарий:

Доказательство неверно. Я остановлюсь на том, в чем именно заключается ошибка. Для этого мне нужно время. Я размещу объяснение на своей домашней странице

URL-адрес домашней страницы: http://theory.cs.uni-bonn.de/blum/blum.var

Но на момент написания статьи ничего актуального нет. Пока доказательство показано некорректным противоречием.

Я ожидаю, что из этой работы получится что-то полезное, даже если это не будет доказательство P≠NP.

Именно так лучше всего работают математика и наука.

Обновление 2, 26 августа

Скотт Ааронсон опубликовал, среди прочего, краткое изложение текущего состояния экспертизы доказательства.

…Только интеллектуальная честность заставляет меня сообщить, что примерно к пятнице прошлой недели — т.е. точно в предсказанный мною срок — среди экспертов сложился четкий консенсус относительно того, что доказательство P≠NP Блюма имеет непоправимые недостатки, и с тех пор этот консенсус сохраняется

Далее он продолжает:

Предыстория попытки Блюма, контрпример, показывающий, что доказательство должно где-то провалиться, и особенности того, что, по-видимому, идет не так, уже были подробно рассмотрены в других местах: см. особенно пост Луки, пост Дика Липтона, пост Джона Баэза и тему CS Theory StackExchange.

Он также кратко объясняет, почему доказательство должно быть неудачным — потому что если бы оно работало, то его можно было бы применить к конкретной функции, функции Тардоса, и получить противоречие о том, что она не находится в P, когда доказано, что она находится. Подробнее об этом читайте в остальной части статьи: HTTPS / Курц / eclipse / Шарлотсвилль / Блюм / P vs. NP

Обновление 1

Теперь у нас есть новый комментарий к статье и предстоящему затмению (!) на блоге Gödel’s Lost Letter and P=NP — обязательном блоге по теории сложности, написанном Диком Липтоном и Кеном Риганом из Computer Science at Georgia Tech. Общее мнение, выраженное в блоге, состоит в том, что в доказательстве есть много неясных мест и общее ощущение беспокойства, но не настолько, чтобы сказать, что оно неверно.

Один из интересных комментариев к доказательству таков:

В более общем смысле, даже если доказательство несовершенно, содержит ли оно новые идеи, которые могут пригодиться в будущем? В доказательстве Блюма утверждается очень сильная нижняя граница {2^{omega(N^{1/6})}} на сложность схемы, определяющей, имеет ли граф из {N} ребер клику размера {N^{1/3}}. Он получает нижнюю границу {2^{tilde{omega}(N^{1/4})}} для другой функции, в которой {tilde{omega}(N^{1/4})} для другой функции, где тильда означает до коэффициентов {log N} в экспоненте. Мы были бы очень рады, если бы он доказал, что эта функция имеет суперлинейную булеву сложность.

Конец обновлений по P≠NP

Новая статья Норберта Блюма, нынешнего заведующего кафедрой информатики Боннского университета, «Решение проблемы P против NP» появилась в arXiv. Неясно, была ли она подана в реферируемый журнал, но это не помешало людям начать спорить о ней. Если вы не математик, то вас может удивить то, насколько сомнительна вся система доказательства теорем. Можно было бы предположить, что подобная статья сразу же вызовет интерес, и последуют авторитетные комментарии, но доказательств слишком много, а проверка требует времени.

Например, Скотт Ааронсон (Scott Aaronson), который написал краткое изложение всей этой полемики и является универсальным специалистом по таким вопросам, опубликовал следующее обновление в совершенно не связанном с ней блоге:

Несвязанное обновление: Всем, кто продолжает спрашивать меня о «новом» доказательстве P≠NP: Я бы снова поставил $200,000 на то, что статья не устоит, за исключением того, что в прошлый раз, когда я пытался это сделать, это не достигло своей цели, которая заключалась в том, чтобы заставить людей перестать спрашивать меня об этом. Поэтому: пожалуйста, перестаньте спрашивать, и если к концу недели эта вещь не будет опровергнута, вы можете вернуться и сказать, что я был закрытым дураком.

Проблема усугубляется тем, что люди, которые должны знать, что делают, подготовили несколько некачественных работ. Кажется, что слишком легко убедить себя в том, что ты доказал что-то важное в этом вопросе, даже если ты эксперт.

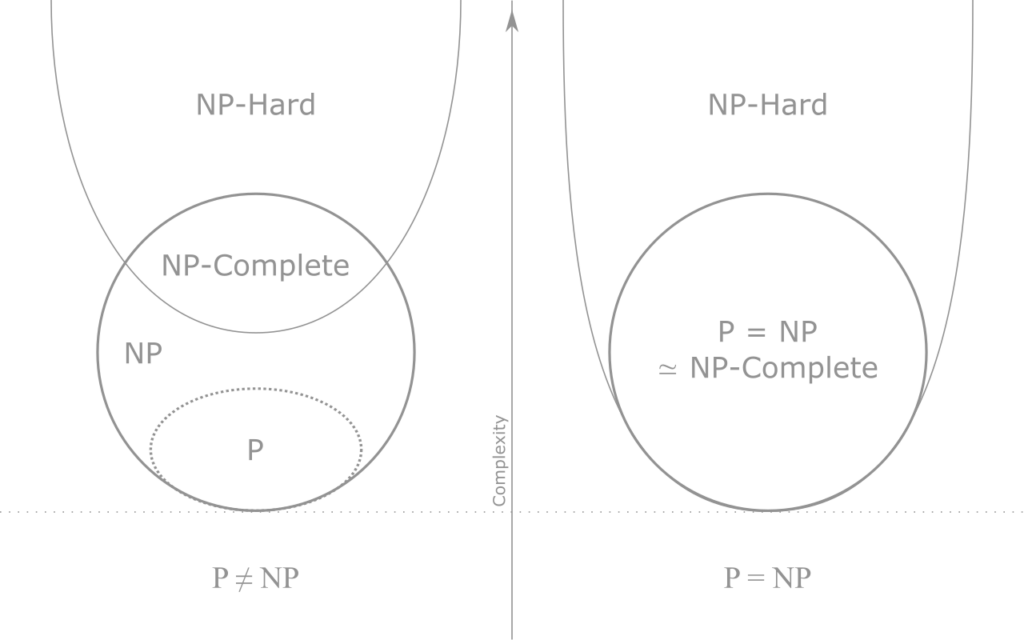
Конечно, доказательство того, что P≠N — это наименее захватывающий вариант, хотя он и претендует на премию Клэя в миллион долларов. Наименее интересным он является потому, что именно этого ожидает большинство ученых-компьютерщиков.

NP-задача — это задача, которую трудно решить, но легко проверить, если вам дано решение. Например, вам дано логическое выражение в 1000 переменных, и ваша задача — найти набор значений 0/1, который делает выражение истинным. Чтобы найти решение, нужно перебрать все значения, что займет много времени, но если я дам вам предложенное решение, то проверить, является оно решением или нет, очень просто — достаточно подставить значения в выражение и посмотреть, истинно ли оно.

Другой пример — факторизация. Если я дам вам большое число и попрошу найти его простые коэффициенты, то единственным способом найти решение будет поиск делителей, а это занимает много времени. Если же я дам вам список делителей, то вы сможете проверить его в кратчайшие сроки, просто разделив число на каждый из них по очереди.

Что привлекает в этих NP-задачах, так это простота проверки решения. Кажется, что решение гораздо ближе, чем можно предположить при его поиске. Это наводит некоторых людей на мысль, что NP-задачи на самом деле не так сложны, как кажется, и уж точно не так сложны, как задачи, решения которых трудно найти и трудно проверить. Это побуждает людей доказывать, что NP=P, и шокировать всех. Конечно, если учесть, что большинство наших кодов и механизмов защиты в Интернете зависят от того, что NP-проблемы легко проверить и трудно решить, это было бы практической катастрофой.

Чаще всего считается, что NP-задачи сложны по своей сути, дело не в том, что мы просто не нашли алгоритм. Они могут быстро проверяться, но то, что найти решение в первую очередь сложно, — это факт природы.

Именно это и доказывает последняя работа:

Берг и Ульфберг, Амано и Маруока с помощью CNFDNF-аппроксиматоров доказали экспоненциальные нижние границы для монотонной сетевой сложности функции клики и функции Андреева. Мы показываем, что эти аппроксиматоры могут быть использованы для доказательства такого же нижнего предела для их немонотонной сетевой сложности. Из этого следует P≠NP.

В настоящее время жюри сетевой дискуссии, похоже, не определилось. Некоторые ранние возражения против доказательства были сняты, но появились и другие. В целом высказывается скептическое мнение, что статья слишком проста, чтобы быть правдой. Если бы все дело было только в этом, то доказательство должно было бы появиться уже давно — но это не контрдоказательство. По-прежнему удивительно, что доказательство не может быть объявлено хорошим или плохим за короткое время — то, что это невозможно, почти противоречит самой идее доказательства.

Следите за новостями по мере проведения анализа.

</div