DTW简介

DTW（Dynamic Time Warping）是一种用于比较时间序列之间相似性的算法。它可以有效地处理在时间轴上存在偏移、缩放和扭曲等变形的时间序列数据。DTW算法通过对两个时间序列进行动态规整，将它们按最优路径进行对齐，并计算它们之间的距离度量值。DTW算法被广泛应用于语音识别、图像识别、信号处理、生物信息学等领域。一个时间序列“扭曲”到一个示例如图所示：

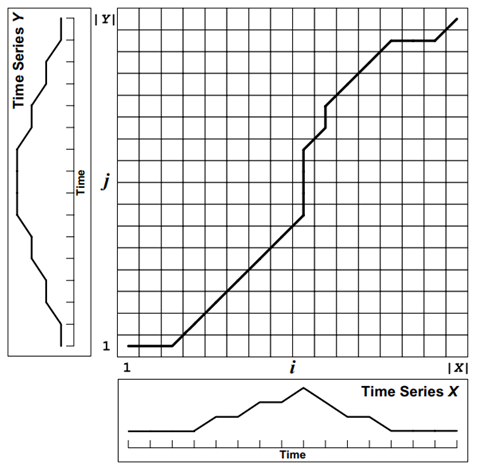
论文地址：https://irit.fr/~Julien.Pinquier/Docs/TP_MABS/res/dtw-sakoe-chiba78.pdf

DTW基本原理

在时间序列中，需要比较相似性的两段时间序列的长度可能并不相等，在语音识别领域表现为不同人的语速不同。而且同一个单词内的不同音素的发音速度也不同，比如有的人会把‘A’这个音拖得很长，或者把‘i’发的很短。另外，不同时间序列可能仅仅存在时间轴上的位移，亦即在还原位移的情况下，两个时间序列是一致的。在这些复杂情况下，使用传统的欧几里得距离无法有效地求的两个时间序列之间的距离(或者相似性)。

DTW通过把时间序列进行延伸和缩短，来计算两个时间序列性之间的相似性：

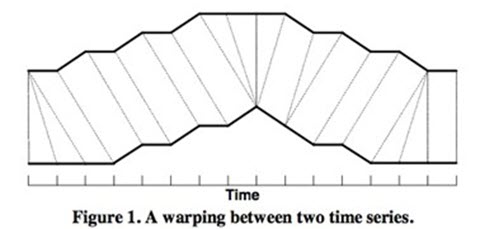
如上图所示，上下两条实线代表两个时间序列，时间序列之间的虚线代表两个时间序列之间的相似的点。DTW使用所有这些相似点之间的距离的和，称之为归整路径距离(Warp Path Distance)来衡量两个时间序列之间的相似性。

假设我们有两条时间序列X和Y，它们分别表示为：

$$X=x_1,x_2,…,x_N​$$

$$Y=y_1,y_2,…,y_M$$

其中N和M分别是序列X和Y的长度。DTW算法的目的是找到一个最优的对齐路径，使得序列X和Y之间的距离度量值最小化。

假设我们使用$d(i,j)$表示序列$X_i$和$Y_j$之间的距离度量值，其中i = 1,…,N；j = 1,…,M。则DTW算法的核心就是在保证对齐路径连续和单调上升的条件下，计算最小距离度量值。

具体地，可以通过以下3个步骤来实现DTW算法：

• 初始化对齐路径的起点和终点为(1,1)和(N,M)，并定义一个二维矩阵D，其中$D(i, j)$表示序列$X_i$和$Y_j$之间的最小距离度量值。
• 递归计算矩阵D中每个元素的值，并选择路径上的最小值。公式如下：$D(i,j)=d(i,j)+min(D(i-1,j),D(i,j-1),D(i-1,j-1))$，其中d(i,j)表示序列$X_i$和$Y_j$之间的距离度量值，min()函数表示取三个参数的最小值。
• 最后，在矩阵D中沿最优路径从（1,1）到（N，M）遍历，即可得到最小距离度量值。

DTW算法是如何工作的？

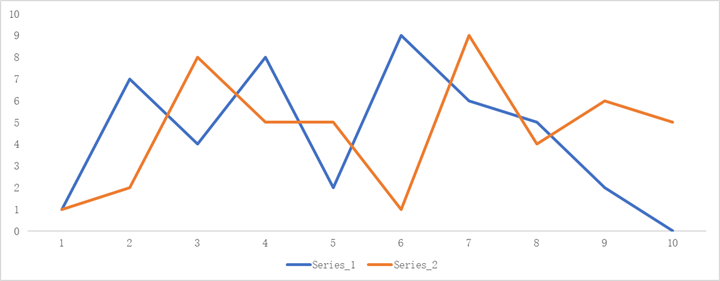
让我们取两个时间序列信号A和B。

Time	Series_1	Series_2
1	1	1
2	7	2
3	4	8
4	8	5
5	2	5
6	9	1
7	6	9
8	5	4
9	2	6
10	0	5

步骤1：创建空成本矩阵

创建一个空的成本矩阵M，用x和y标签作为两个序列的振幅来进行比较。

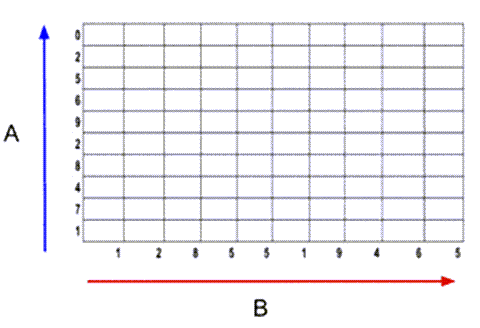
第2步：成本计算

使用下面提到的公式从左角和底角开始填充成本矩阵。

$$M(i, j) = |A(i) – B(j)| + min (M(i-1,j-1), M(i, j-1), M(i-1,j))$$

• i是A系列的迭代器
• j是B系列的迭代器

计算结果如下：

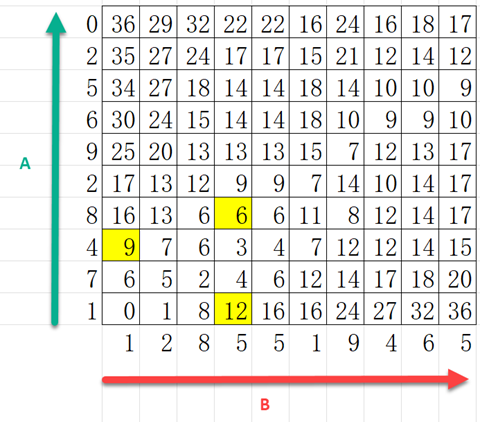
表格中的数值是如何产生的，我们以标颜色的6、9和12来说明：

• 对于6：|8 -5| + min(6, 6, 3) = 6
• 对于9：|4 -1| + min(6) = 9
• 对于12：|1 -5| + min(8) = 12

首先是取两个序列值的对应差，然后加左下角L行中3个值中的最小值。

第3步：确定翘曲路径

识别从矩阵的右上角开始，遍历到左下角的翘曲路径。遍历路径的确定是基于具有最小值的邻居。

在我们的例子中，它从17开始，在其邻居18、14和12中寻找最小值，即12。

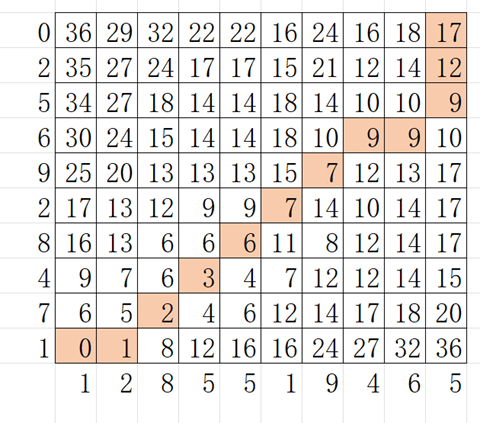
最终路径如上图颜色所示。

让我们把这个翘曲路径系列称为d。

d = [17, 12, 9, 9, 9, 7, 7, 6, 3, 2, 1, 0]

第四步：最终距离计算

时间归一化的距离，D

$$D = \frac{\sum_{i=1}^{k}d(i)}{\sum_{i=1}^{k}k}$$

其中k是序列d的长度。在我们的例子中，k=12。

D = (17 + 12 + 9 + 9 + 9 +7 + 7 + 6 + 3 + 2 +1 + 0)/12=6.8333

DTW算法的优点和缺点

DTW算法具有以下优点：

• 能够有效地处理在时间轴上存在偏移、缩放和扭曲等变形的时间序列数据；
• 可以处理不同长度的时间序列，因此更加灵活；
• 算法简单易懂，容易实现。

但是，DTW算法也存在一些缺点：

• 对于长时间序列而言，计算复杂度很高，因此需要占用大量的计算资源；
• 算法在寻找最优路径时，可能会受到局部极小值的影响，导致结果不够准确；
• 算法对于噪声和异常值比较敏感，可能会带来一定的误差。

DTW算法伪代码实现

int DTWDistance(s: array [1..n], t: array [1..m]) {
    DTW := array [0..n, 0..m]

    for i := 1 to n
        DTW[i, 0] := infinity
    for i := 1 to m
        DTW[0, i] := infinity
    DTW[0, 0] := 0

    for i := 1 to n
        for j := 1 to m
            cost:= d(s[i], t[j])
            DTW[i, j] := cost + minimum(DTW[i-1, j  ],    // insertion
                                        DTW[i  , j-1],    // deletion
                                        DTW[i-1, j-1])    // match

    return DTW[n, m]
}

DTW算法Python实现

Github地址：https://github.com/pierre-rouanet/dtw

import numpy as np
from dtw import dtw

x = np.array([2, 0, 1, 1, 2, 4, 2, 1, 2, 0])
y = np.array([1, 1, 2, 4, 2, 1, 4, 2])
manhattan_distance = lambda x, y: np.abs(x - y)

d, cost_matrix, acc_cost_matrix, path = dtw(x, y, dist=manhattan_distance)
print(d)

FastDTW简介

DTW采用动态规划来计算两个时间序列之间的相似性，算法复杂度为$O(N^2)$。当两个时间序列都比较长时，DTW算法效率比较慢，不能满足需求，为此，有许多对DTW进行加速的算法：FastDTW,SparseDTW,LB_Keogh,LB_Improved等。在这里我们介绍FastDTW。

FastDTW之前的优化方案

FastDTW之前，后来主要有两种近似计算DWT的算法，损失一定准确率的前提下减少时间和空间复杂度：

1、约束 – 限制在成本矩阵中评估的单元数

典型有两种：constraints: Sakoe-Chiba Band (left) and Itakura Parallelogram (right)

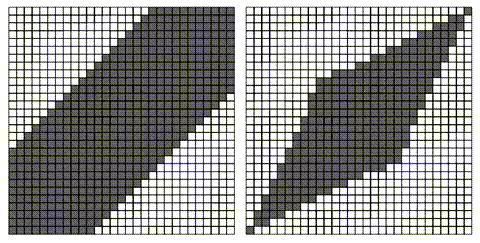
很明显，缺点是当全局最优解不在band内时，就有误差。图中的阴影区域是成本矩阵的单元格，它们被填充由每个约束的 DTW 算法。每个阴影区域或窗口的宽度由参数指定。当使用约束时，DTW 会通过约束窗口找到最优的扭曲路径。但是，如果全局最优扭曲路径不完全在窗口内，则将无法找到它。使用约束以一个常数因子加速 DTW，但如果窗口大小是时间序列长度的函数，则 DTW 仍然是$O(N^2)$。约束在时间序列的时间对齐只有很小差异的领域中效果很好，并且最佳扭曲路径预计接近线性扭曲并以相对直线对角线穿过成本矩阵。但是，如果时间序列是在完全不同的时间开始和停止的事件，则约束效果不佳。在这种情况下，warp 路径可能会偏离线性 warp 很远，并且必须评估几乎整个成本矩阵以找到最佳 warp 路径。

下图描述了约束 DTW 不能很好地工作的情况的简化示例，必须评估整个成本矩阵以获得良好的结果。这可能发生在时间序列是受监控设备的应用程序中，这些设备以可预测的顺序发出命令（例如开/关），但命令之间的时间量（稳态条件）未指定。此类数据的示例包括航天飞机阀门特征。

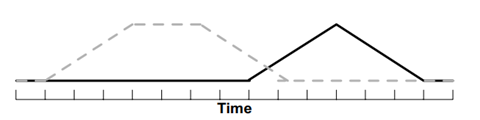
2、抽象——对数据的简化表示执行 DTW

这种方法作者在FastDTW中也用上，如图所示，就是在低分辨率的矩阵中求解，也会有误差，因为路径不够细化。

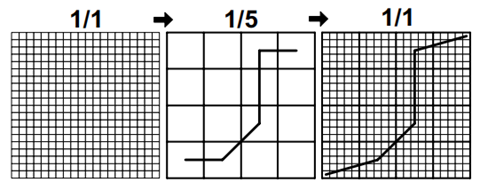
抽象通过对数据的简化表示进行操作来加速 DTW 算法。这些算法包括 IDDTW 、PDTW 和 COW 。时间序列的大小被缩小以使成本矩阵更易于计算。为较低分辨率的时间序列找到了一个扭曲路径并被映射回到全分辨率。

由此产生的加速取决于使用了多少抽象。显然，计算出的翘曲路径随着抽象级别的增加，它变得越来越不准确。投影低分辨率扭曲全分辨率的路径通常会创建一个远非最佳的扭曲路径。这是因为即使如果最优扭曲路径通过低分辨率单元，则将扭曲路径投影到更高的分辨率忽略了扭曲路径中可能非常重要的局部变化。因此不适用于局部变化剧烈的序列。

FastDTW使用下面三种方法进行改进：

• 粗化——将时间序列缩小为更小的时间序列，以更少的数据点尽可能准确地表示相同的曲线。
• 投影——在较低分辨率下找到最小距离扭曲路径，并将其用作更高分辨率最小距离扭曲路径的初始猜测。
• 细化——通过局部调整扭曲路径来优化从较低分辨率投影的扭曲路径。

FastDTW中的分级使用更高分辨率计算，弥补了之前的Abstract的方法，原来只使用一次降低分辨率；FastDTW中的细化使用半径参数控制，弥补原来的Band的方法那种不灵活性，因为Band的方法需要依靠先验知识判断最优路径大概在那些位置；而半径参数只是作为分级粗化投影的一个补充。

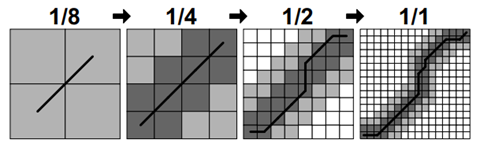
如图所示具体如下：粗化通过平均相邻的点对来减少时间序列的长度（或分辨率）。生成的时间序列比原始时间序列小两倍。粗化运行多次以产生时间序列的不同分辨率。投影采用以较低分辨率计算的扭曲路径，并以较高的分辨率确定它通过的单元格。由于分辨率增加了两倍，因此低分辨率扭曲路径中的单个点将映射到更高分辨率的至少四个点（如果 |X| = |Y |，则可能 > 4）。然后在细化过程中将此投影路径用作启发式方法，以找到更高分辨率的扭曲路径。细化在投影路径的邻域中找到最佳的扭曲路径，其中邻域的大小由半径参数控制。在我们的多级方法中，成本矩阵仅填充在从先前分辨率投影的路径的附近。由于扭曲路径的长度随着时间序列的长度线性增长，我们的多级方法是 O(N) 算法。 FastDTW 算法首先使用粗化来创建将被评估的所有分辨率。图中显示了一个时间序列上的例子在运行 FastDTW 算法时创建的四个分辨率（使用多少个分辨率的粗化矩阵按照实际序列长度确定）。

在图中，从 1/8 分辨率的扭曲路径的投影显示为 1/4 分辨率的重度阴影单元。为了细化投影路径，使用非常具体的约束运行受约束的 DTW 算法，即仅评估投影扭曲路径中的单元格。这将通过从较低分辨率投影的扭曲路径区域找到最佳扭曲路径。然而，全局最优扭曲路径可能不完全包含在投影路径中。为了增加找到全局最优解的可能性，有一个半径参数来控制投影路径每一侧上的额外单元数，这些单元格也将在优化扭曲路径时进行评估。在图 中，半径参数设置为 1。由于半径而在扭曲路径细化过程中包含的单元格被轻微着色。一旦以 1/4 分辨率细化扭曲路径，该扭曲路径将投影到 1/2 分辨率，扩大半径 1，然后再次细化。最后，将扭曲路径投影到图 中的全分辨率 (1/1) 矩阵。投影被半径扩展并最后一次细化。这个细化的扭曲路径是算法的输出。 FastDTW 在所有分辨率下评估了 4 + 16 + 44 + 100 = 164 个单元，而 DTW 评估了 256 (162) 个单元。对于这个小问题，效率的提高并不是很显着，尤其是考虑到创建所有四个分辨率的开销，在长序列有很大差距。然而，FastDTW 评估的单元数与时间序列的长度成线性关系，而经典的动态时间扭曲算法总是评估O(N^2)个单元（如果两个时间序列的长度均为 N）。

代码实现：

论文地址：http://cs.fit.edu/~pkc/papers/tdm04.pdf

FastDTW的代码示例

项目地址：https://github.com/slaypni/fastdtw

代码示例：

import numpy as np
from scipy.spatial.distance import euclidean

from fastdtw import fastdtw

x = np.array([[1, 1], [2, 2], [3, 3], [4, 4], [5, 5]])
y = np.array([[2, 2], [3, 3], [4, 4]])
distance, path = fastdtw(x, y, dist=euclidean)
print(distance)

DTW库比较

先给测试数据：

Python包	平均执行时间	标准差
dtaidistance distance_fast	0.00011	0.00032
TSLearn	0.00021	0.00042
PyTS	0.00031	0.00046
DTW-Python	0.00144	0.00049
dtaidistance	0.03292	0.00171
FastDTW	0.05874	0.00246

可以看到FastDTW并没有其他包表现的那么出色，但是并不能说明FastDTW是不好的，这还需结合数据集下面运行后的结果做评测。

dtaidistance

dtaidistance是一个Python中的时间序列距离计算库，提供了多种距离度量方法和动态时间规整（DTW）算法的实现。它可以用于处理时间序列数据的相似性分析、聚类、分类等任务。

dtaidistance支持以下常见的时间序列距离度量方法：

• Euclidean：欧几里得距离，即两个时间序列之间点对点的欧式距离；
• Manhattan：曼哈顿距离，即两个时间序列之间点对点的曼哈顿距离；
• Chebyshev：切比雪夫距离，即两个时间序列之间点对点的切比雪夫距离；
• Minkowski：明可夫斯基距离，可用于在不同维度上加权考虑距离度量；
• Pearson：皮尔逊相关系数，可用于比较两条时间序列之间的线性关系。

dtaidistance提供了三种DTW算法的实现：

• 快速DTW（FastDTW）：通过使用特定的启发式策略和剪枝技术来减少计算时间，通常比标准DTW算法更快，并且可以在处理大型时间序列时提供更好的性能；
• 多尺度DTW（MultiscaleDTW）：将时间序列分解为多个尺度，并对每个尺度应用DTW算法，从而提高算法的鲁棒性和效率；
• 惩罚DTW（WarpingPathDTW）：在计算DTW距离时，额外惩罚路径偏移和扭曲，以尽可能使对齐路径保持连续和单调上升。

dtaidistance具有以下优点：

• 支持多种距离度量方法，可以根据不同的任务需求进行选择；
• 提供快速DTW、多尺度DTW和惩罚DTW等不同的DTW实现，可以根据数据大小和复杂性进行选择；
• 算法简单易懂，易于使用和扩展。

但是，dtaidistance也存在一些缺点：

• 对于长时间序列而言，计算复杂度仍然较高，因此需要占用一定的计算资源；
• 算法对于噪声和异常值比较敏感，可能会带来一定的误差；
• 目前还不支持GPU加速，因此在处理大型数据时，可能会受到计算速度的限制。

使用示例：

from dtaidistance import dtw
import numpy as np

a = np.random.random(100)
b = np.random.random(200)

distance = dtw.distance(a, b)
print(f"DTW Distance: {distance}")
如果觉得上面的方法有些慢，可以使用：
distance = dtw.distance_fast(a, b)
print(f"DTW Distance: {distance}")

TSLearn

TSLearn是一个Python中的时间序列分析库，它提供了各种时间序列处理方法和机器学习算法的实现。TSLearn可以用于多种应用场景，例如时间序列分类、聚类、预测等任务。

TSLearn支持以下常见的时间序列处理方法和机器学习算法：

• 特征提取：TSLearn提供了多种特征提取方法，如峰值、波形长度、自相关等，可以将原始时间序列转化为一组有意义的特征向量；
• 相似性度量：TSLearn支持多种相似性度量方法，例如欧几里得距离、动态时间规整（DTW）距离、曼哈顿距离等，可以用于比较不同时间序列之间的相似性；
• 时间序列分类和聚类：TSLearn提供了多种分类和聚类算法，如KNN、SVM、随机森林、k-means等，可用于将时间序列进行分组或划分；
• 时间序列预测：TSLearn支持多种时间序列预测方法，如ARIMA模型、LSTM网络等，可用于预测未来时间序列的趋势和变化。

代码示例：

from tslearn.metrics import dtw as ts_dtw
import numpy as np

a = np.random.random((100, 2))
b = np.random.random((200, 2))

distance = ts_dtw(a, b)
print(f"DTW Distance: {distance}")

PyTS DTW

PyTS DTW是一个Python中的时间序列距离计算库，它提供了多种基于动态时间规整（DTW）的距离度量方法。PyTS DTW可以用于处理时间序列数据的相似性分析、聚类、分类等任务。

PyTS DTW支持以下常见的基于DTW的时间序列距离度量方法：

• DTW：经典的动态时间规整算法，通过对两个时间序列进行动态规整，将它们按最优路径进行对齐，并计算它们之间的距离度量值；
• WDTW：权重动态时间规整算法，引入权重系数来平衡两条时间序列在DTW路径上不同位置的距离贡献；
• SINKHORN：Sinkhorn距离算法，通过迭代过程逼近两个时间序列之间的极小距离度量值；
• MSM：移动窗口匹配算法，将时间序列划分为多个子序列，并对每个子序列应用DTW算法，从而减少算法的计算复杂度。

PyTS DTW具有以下优点：

• 支持多种基于DTW的距离度量方法，可以根据不同的任务需求进行选择；
• 算法简单易懂，易于使用和扩展；
• 提供了可视化工具和示例代码，可帮助用户快速上手并理解算法原理。

但是，PyTS DTW也存在一些缺点：

• 对于长时间序列而言，计算复杂度仍然较高，可能需要占用大量的计算资源；
• 算法对于噪声和异常值比较敏感，需要对数据进行预处理和清洗；
• 部分算法的可调参数较多，需要进行参数调优才能达到最佳效果。

使用示例：

from pyts.metrics import dtw
import numpy as np

a = np.random.random((100, 2))
b = np.random.random((200, 2))

distance = dtw(a, b)

print(f"DTW Distance: {distance}")

DTW-Python

DTW-Python是一个基于Python的动态时间规整（DTW）算法库，用于计算两个时间序列之间的距离度量值。它提供了多种DTW算法的实现和可视化工具，可用于处理时间序列数据的相似性分析、聚类、分类等任务。

DTW-Python提供了以下常见的DTW算法的实现：

• 经典DTW：通过对两个时间序列进行动态规整，将它们按最优路径进行对齐，并计算它们之间的距离度量值；
• 快速DTW：通过使用特定的启发式策略和剪枝技术来减少计算时间，通常比标准DTW算法更快，并且可以在处理大型时间序列时提供更好的性能；
• 条件DTW：在计算DTW距离时，引入一些先验信息来约束对齐路径，从而提高算法的准确性和鲁棒性；
• 级联DTW：将时间序列划分为多个子序列，并对每个子序列应用DTW算法，从而减少算法的计算复杂度。

DTW-Python具有以下优点：

• 支持多种DTW算法的实现，可以根据不同的任务需求进行选择；
• 提供可视化工具和示例代码，可帮助用户快速上手并理解算法原理；
• 代码简单易懂，易于使用和扩展。

但是，DTW-Python也存在一些缺点：

• 对于长时间序列而言，计算复杂度仍然较高，可能需要占用大量的计算资源；
• 算法对于噪声和异常值比较敏感，需要对数据进行预处理和清洗；
• 目前还不支持GPU加速，因此在处理大型数据时，可能会受到计算速度的限制。

代码示例：

from dtw import dtw
import numpy as np

a = np.random.random((100, 2))
b = np.random.random((200, 2))

alignment = dtw(a, b)

print(f"DTW Distance: {alignment.distance}")