[Tutorial] Zeta, Mobius Transform to AND, OR, GCD Convolution

Introduction

Original Post(Korean)

For those who have studied the Inclusion-Exclusion Principle or the Mobius Inversion formula, you may have wondered about the definition of and the process of offsetting unnecessary values by multiplying . Although it is possible to show the validity of these formulas through expansion, such proofs lack intuitive clarity.

In this article, I will define Zeta and Mobius Transform on a Poset and explore examples from various Posets. Understanding these concepts will provide insights into the Inclusion-Exclusion Principle and the Mobius Inversion formula. Additionally, Zeta and Mobius Transform are essential concepts connected to SOS DP and AND, OR, GCD, LCM Convolution. In the final part of the article, we will examine interesting connections to various convolutions from Zeta and Mobius Transform.

Table of Contents

1. What is Poset?
2. Zeta, Mobius Transform on Poset ( ↔ )
3. Definition of Mobius function ()
4. Examples
5. Fast Zeta, Mobius Transform
6. → convolution →

1. What is Poset?

A Poset (, ) is a set with a relation that satisfies the following properties.

• Reflexive: For all , .
• Antisymmetric: If and , then .
• Transitive: If and , then .

There may be pairs of for which the operator is not defined. For example, in , although and hold, there might be no defined relationship between and . For this reason, (, ) is referred to as a Partially Ordered Set (Poset).

Posets can be effectively visualized using Directed Acyclic Graphs (DAG). Placing the elements of as vertices and representing pairs where and as edges , we can obtain a DAG. To simplify the visualization, we exclude self-loops ( → ) and redundant edges (e.g., → when → and → are present) and create a Hasse Diagram, which succinctly represents the relationship between elements.

In the upcoming sections, the descendant relationship of vertices will be crucial for the Zeta and Mobius Transform. A vertex is considered a descendant of if there exists a path from to .

2. Zeta, Mobius Transform on Poset ( ↔ )

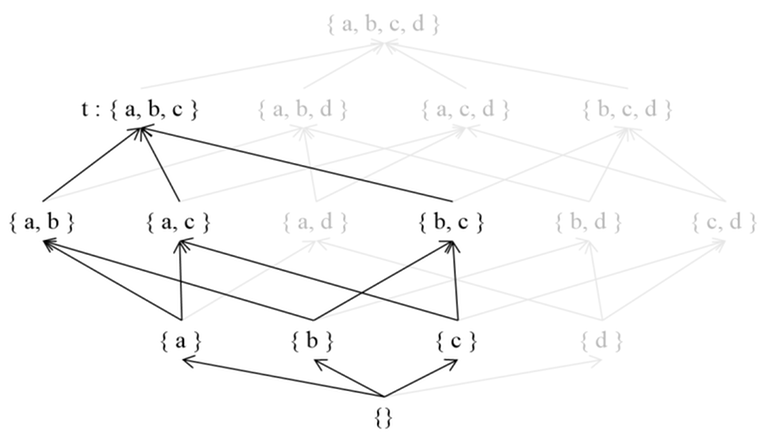
In a Poset (, ), let's define as follows.

Here, is defined as the sum of for all such that . In other words, represents the sum of values for the descendants of . For instance, is equal to . To simplify, we can define as if and otherwise, allowing us to remove the condition from the summation expression.

This process of obtaining values from the given values is called the Zeta Transform.

Now, we want to find an appropriate function that satisfies the above equation and enables us to reconstruct the values of from the given values.

The process of obtaining values from the given values is called the Mobius Transform.

3. Definition of Mobius function ()

The function can be defined recursively as follows.

Let's understand the significance of the function's definition in the context of a Poset's DAG.

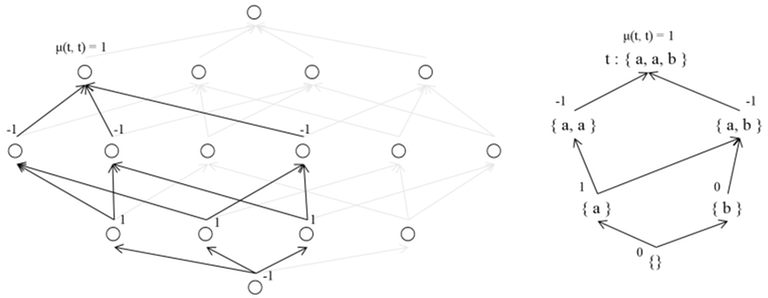
Starting from and moving along the backward edges in topological order, let's determine for each . The value of is . For , we can calculate the value of such that for , which represents ancestors of and descendants of , we find the sum of and multiply it by .

By the definition, the function has the property that sum of all for all equals only if ; otherwise, it is always . From a DAG perspective, if we fix and select an arbitrary descendant of which is not , the sum of all values between and will always be . This property is essential to the function and allows it to be used in the Mobius Transform.

Now, let's prove the validity of the Mobius Transform equation.

By expressing the property of the function using the function, the sum of is equal to . Here, represents the Iverson bracket, which evaluates to if the inner statement is true and otherwise.

After expanding the Mobius Transform equation, we can use the above property to show the contribution of to the entire equation is . The variable appears once for each where , and is multiplied by before being added to the overall equation. The contribution of in the entire equation depends on the sum of for . Through the previous discussion, we know that this contribution is only when . ■

Therefore, the function is suitable for the Mobius Transform.

4. Examples

The method to calculate in a Poset (, ) can vary depending on how and are defined.

In this section, we will calculate in various (, ) definitions and find the Zeta and Mobius Transform formulas.

1. When is a set and is the subset relation

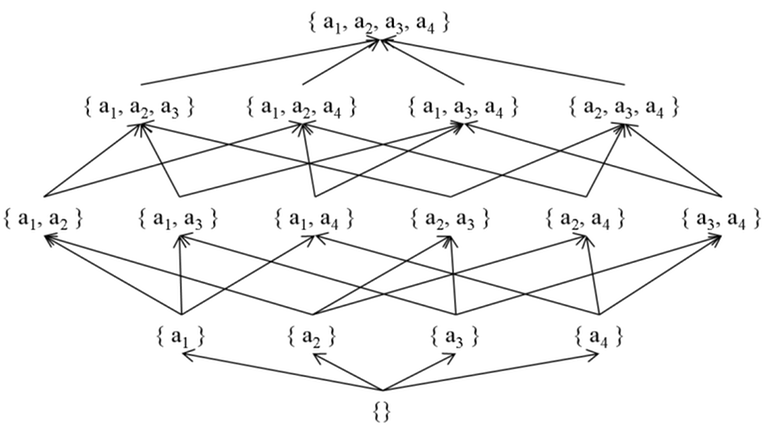
Using the definition of , for , is .

Proof: The proof begins with the base case where , and then uses mathematical induction on . Let where is ancestor of and descendant of . The number of such is . Assuming that , we find that is equal to . Using the binomial theorem and simplifying the expression, we obtain . ■

can be obtained by iterating over the subsets of and adding , and can be obtained by iterating over the subsets of and adding .

2. When is a set and is the superset relation

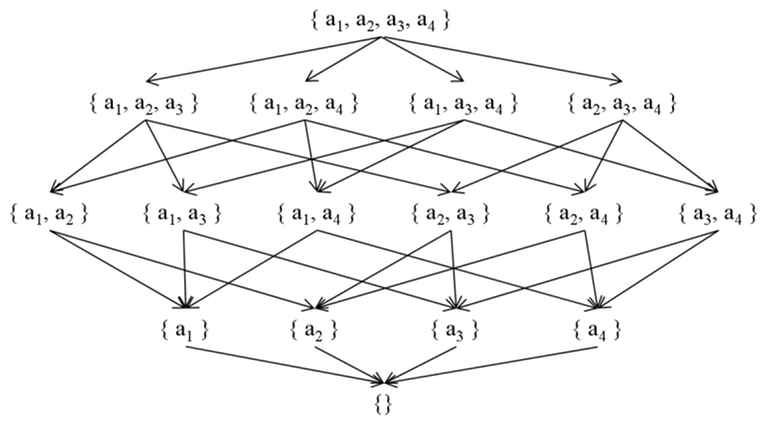
In this case, is (superset) instead of (subset). Since the direction of the relation is reversed, the Hasse Diagram corresponding to the Poset also has its edges reversed.

For two Posets where the relations are opposite, and functions in the original Poset can be related to , functions in the transformed Poset as follows: and .

Proof: The proof is trivial for the function. For the function, we can use the fact that is equivalent to the definition of . Using this, showing is enough. Treating and as elements of a matrix, we have , which implies that and are inverse matrices. From , we can also deduce , so the sum of for where is . ■

Therefore, for , is .

can be obtained by iterating over the supersets of and adding , and can be obtained by iterating over the supersets of and adding .

Problem: https://www.acmicpc.net/problem/17436

Solution: http://boj.kr/02f08c67d80a4e28aa5847e1fa0c05cb

3. When is (natural numbers) and is the divisor relation

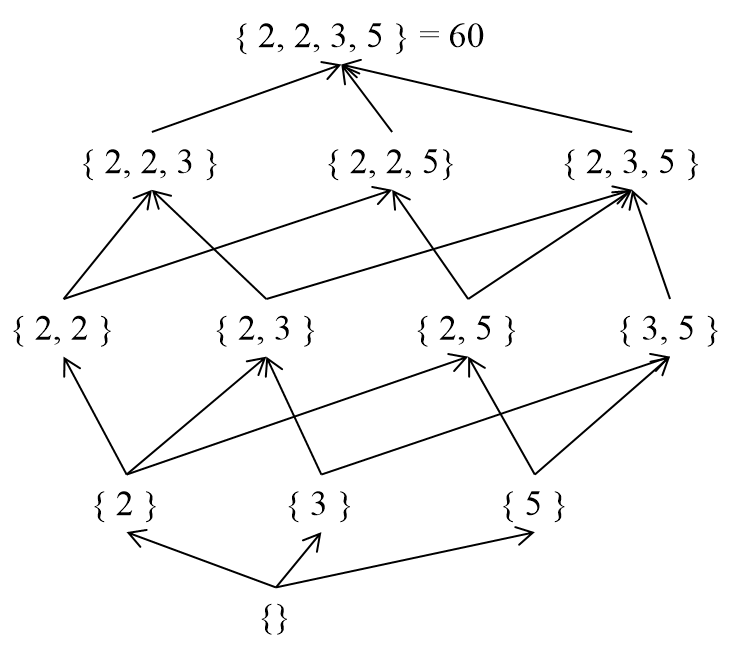
In this case, when , is equal to . Here, is the Mobius function in number theory. If has no square factors, then is equal to , where is the number of prime factors of . Otherwise, is .

(Reference: https://en.wikipedia.org/wiki/M%C3%B6bius_function)

Proof: We can represent as , and view it as a multiset (with occurring times). We can then consider the relation (meaning is divisible by ) as a relation on the set. We will apply mathematical induction on . When , can be expressed as . First, let's consider the case where the multiset of has no duplicate elements. By assuming that is , we find that , where is the number of prime factors of . There are multisets where k is the number of prime factors of , so . If the multiset of contains duplicate elements, we can consider the multiset obtained by removing the duplicate elements. For any , the sum of the values of is , so . ■

can be obtained by iterating over the divisors of and adding , and can be obtained by iterating over the divisors of and adding .

4. When is (natural numbers) and is the multiple relation

In this case, the relation is multiple instead of divisor. Since the direction of the relation is reversed, for , .

can be obtained by iterating over the multiples of and adding , and can be obtained by iterating over the multiples of and adding .

The number of multiples of is infinite, so in most cases, we establish a condition such as for . This way, we only need to consider , and the set is restricted to , which ensures the convergence of the formulas.

Problem: https://www.acmicpc.net/problem/16409

Solution: http://boj.kr/255776b11c7a4ce7927cb19b00acbaf0

5. Fast Zeta, Mobius Transform

In the previous section, we defined the and functions in a Poset using several examples and used the Zeta and Mobius Transformations to find the single value of and . This method works efficiently when we calculate only one value.

Now, let's consider the case where we want to find all the values of and . If we use the Zeta and Mobius Transformations times to find values, and if the DAG (Poset's Hasse Diagram) is dense, it would require an operation similar to . However, we can obtain the values of and more efficiently using the special structure of the graph with a prefix sum.

1. Subset Zeta, Mobius Transform

template<typename T>
void SubsetZetaTransform(vector<T>& v) {
	const int n = v.size(); // n must be a power of 2
	for (int j = 1; j < n; j <<= 1) {
		for (int i = 0; i < n; i++)
			if (i & j) v[i] += v[i ^ j];
	}
}

template<typename T>
void SubsetMobiusTransform(vector<T>& v) {
	const int n = v.size(); // n must be a power of 2
	for (int j = 1; j < n; j <<= 1) {
		for (int i = 0; i < n; i++)
			if (i & j) v[i] -= v[i ^ j];
	}
}

Let's assume is the number of elements in the set.

The naive approach would involve traversing all the pairs where , resulting in operations. However, using SOS DP, we can perform the transformation in . SOS DP can be understood as a prefix sum in an -dimensional hypercube.

2. Superset Zeta, Mobius Transform

template<typename T>
void SupersetZetaTransform(vector<T>& v) {
	const int n = v.size(); // n must be a power of 2
	for (int j = 1; j < n; j <<= 1) {
		for (int i = 0; i < n; i++)
			if (i & j) v[i ^ j] += v[i];
	}
}

template<typename T>
void SupersetMobiusTransform(vector<T>& v) {
	const int n = v.size(); // n must be a power of 2
	for (int j = 1; j < n; j <<= 1) {
		for (int i = 0; i < n; i++)
			if (i & j) v[i ^ j] -= v[i];
	}
}

Similarly, the naive approach of traversing all the pairs would require operations, but using SOS DP, we can optimize it to .

3. Divisor Zeta, Mobius Transform

template<typename T>
void DivisorZetaTransform(vector<T>& v) {
	const int n = (int)v.size() - 1;
	for (int p : PrimeEnumerate(n)) {
		for (int i = 1; i * p <= n; i++)
			v[i * p] += v[i];
	}
}

template<typename T>
void DivisorMobiusTransform(vector<T>& v) {
	const int n = (int)v.size() - 1;
	for (int p : PrimeEnumerate(n)) {
		for (int i = n / p; i; i--)
			v[i * p] -= v[i];
	}
}

The number of pairs for which follows the harmonic lemma and is . Thus, even with the naive approach, we can find all the values using operations.

However, by using sieve and prefix sum ideas, we can achieve complexity. (https://noshi91.hatenablog.com/entry/2018/12/27/121649)

In the code, PrimeEnumerate(n) is a function that returns a vector containing all the primes up to . Here is an example implementation.

/* Linear Sieve, O(n) */
vector<int> PrimeEnumerate(int n) {
	vector<int> P; vector<bool> B(n + 1, 1);
	for (int i = 2; i <= n; i++) {
		if (B[i]) P.push_back(i);
		for (int j : P) { if (i * j > n) break; B[i * j] = 0; if (i % j == 0) break; }
	}
	return P;
}

4. Multiple Zeta, Mobius Transform

template<typename T>
void MultipleZetaTransform(vector<T>& v) {
	const int n = (int)v.size() - 1;
	for (int p : PrimeEnumerate(n)) {
		for (int i = n / p; i; i--)
			v[i] += v[i * p];
	}
}

template<typename T>
void MultipleMobiusTransform(vector<T>& v) {
	const int n = (int)v.size() - 1;
	for (int p : PrimeEnumerate(n)) {
		for (int i = 1; i * p <= n; i++)
			v[i] -= v[i * p];
	}
}

Similarly, using the naive approach of traversing all the pairs would require operations, but using sieve and prefix sum, we can optimize it to .

6. → Convolution →

So far, we have learned about Zeta and Mobius Transforms. These two transformations play a role in gathering and restoring information about descendants in a Poset. The Zeta Transform can aggregate information from the descendants of a Poset, while the Mobius Transform can restore the original values from the results of the Zeta Transform.

Now, let's look at the expression . When we expand the expression, it becomes , requiring a total of 9 multiplication operations. However, if we calculate and , we can compute the expression with just 1 multiplication operation. In other words, combining the values and processing them together is faster.

A similar idea can be applied to Zeta and Mobius Transforms. By using the Zeta Transform to aggregate the values of descendants and then using the Mobius Transform to restore them to their original form, we can reduce the number of operations. By using the Zeta and Mobius Transforms mentioned above, we can efficiently implement AND, OR, GCD, and LCM Convolution.

1. AND Convolution

template<typename T>
vector<T> AndConvolution(vector<T> A, vector<T> B) {
	SupersetZetaTransform(A);
	SupersetZetaTransform(B);
	for (int i = 0; i < A.size(); i++) A[i] *= B[i];
	SupersetMobiusTransform(A);
	return A;
}

The AND Convolution algorithm uses the Superset Zeta and Mobius Transforms to efficiently compute the convolution. Given two input arrays and , it computes the array .

Using the Superset Zeta Transform, the function is defined as . Then, the property holds. Superset Zeta and Mobius Transforms can be implemented in , and element-wise multiplication can be done in , resulting in an overall time complexity of for AND Convolution.

Problem: https://judge.yosupo.jp/problem/bitwise_and_convolution

Solution: https://judge.yosupo.jp/submission/153822

2. OR Convolution

template<typename T>
vector<T> OrConvolution(vector<T> A, vector<T> B) {
	SubsetZetaTransform(A);
	SubsetZetaTransform(B);
	for (int i = 0; i < A.size(); i++) A[i] *= B[i];
	SubsetMobiusTransform(A);
	return A;
}

The OR Convolution algorithm uses the Subset Zeta and Mobius Transforms for efficient computation. Given two input arrays and , it computes the array .

Using the Subset Zeta Transform, the function is defined as . Then, the property holds. Similar to AND Convolution, the OR Convolution can also be implemented in time complexity.

Problem: https://www.acmicpc.net/problem/25563

Solution: http://boj.kr/bfe9b18520c048d89126db9912d4c216

3. GCD Convolution

template<typename T>
vector<T> GCDConvolution(vector<T> A, vector<T> B) {
    MultipleZetaTransform(A);
    MultipleZetaTransform(B);
    for (int i = 0; i < A.size(); i++) A[i] *= B[i];
    MultipleMobiusTransform(A);
    return A;
}

The GCD Convolution algorithm uses the Multiple Zeta and Mobius Transforms to efficiently compute the convolution. Given two input arrays and , it computes the array .

The Multiple Zeta Transform is defined as . It can be shown that holds. The Multiple Zeta and Mobius Transforms can be implemented in , resulting in an overall time complexity of for GCD Convolution.

Problem: https://judge.yosupo.jp/problem/gcd_convolution

Solution: https://judge.yosupo.jp/submission/153821

4. LCM Convolution

template<typename T>
vector<T> LCMConvolution(vector<T> A, vector<T> B) {
    DivisorZetaTransform(A);
    DivisorZetaTransform(B);
    for (int i = 0; i < A.size(); i++) A[i] *= B[i];
    DivisorMobiusTransform(A);
    return A;
}

The LCM Convolution algorithm uses the Divisor Zeta and Mobius Transforms for efficient computation. Given two input arrays and , it computes the array .

Divisor Zeta Transform is defined as . It can be shown that , allowing for efficient computation of LCM Convolution in time complexity.

Problem: https://judge.yosupo.jp/problem/lcm_convolution

Solution: https://judge.yosupo.jp/submission/153819

Conclusion

In this article, we explored the concepts of and functions, as well as Zeta and Mobius Transform in the context of Posets. We also looked at several examples of applying them in Convolution.

Zeta and Mobius Transform can be seen as a generalization of the principle of inclusion-exclusion. The Mobius Transform in the case of a Poset defined by sets and the subset relation is the well-known Mobius Inversion in number theory. Understanding this connection can help gain a clearer perspective when solving inclusion-exclusion or Mobius Inversion problems.

As those who have used Mobius Transform in their problems may have felt, the Inclusion-Exclusion Principle is Mobius Transform when Poset is defined as a set and relationship. Also, Mobius Inversion in number theorey is a Mobius Transform in Poset, which is defined by a set of natural numbers and divisor relationship. A better understanding of this will make it more clear to you how you felt dimly when solving inclusion-exclusion or Mobius Inversion problems.

The article briefly introduced Fast Zeta and Mobius Transform without delving into their workings. Techniques like SOS DP (Sum Over Subsets Dynamic Programming) or using Sieve and Prefix Sum to reduce time complexity are worth studying, but I have left that to other resources linked in the article.

AND, OR, GCD, and LCM Convolution are not widely known, and there is limited material explaining them using Zeta and Mobius Transform. Therefore, I included examples of these algorithms at the end of the article. The essence of Convolution algorithms lies in defining a transformation and its inverse, allowing us to replace a time-consuming operation with element-wise multiplication using the transform. The process of collecting information from descendants using Zeta, Mobius Transform, performing computations, and then restoring the original values is intriguing.

Lastly, I did not cover Subset Convolution, which can be implemented in with a slight modification of OR Convolution. I may write about it separately in the future. I also considered including XOR Convolution, but it is more like FFT, where we compute function values and then perform restoration, so I did not cover it here. In my opinion, XOR Convolution is better understood as a multidimensional FFT.

I hope that many readers have gained insights from this article. Thanks for reading!

References: