

曲线艺术编程 coding curves 第十四章 其它曲线(Miscellaneous Curves) - 池中物王...
source link: https://www.cnblogs.com/willian/p/17528280.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

第十四章 其它曲线(Miscellaneous Curves)
原作:Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/
译者:池中物王二狗(sheldon)
曲线艺术编程系列 第十四章
这是系列文章规划的最后一章。如果后面发现其它有趣的曲线类型可能加在这一章。我原计划清单里有几个主题没放出来,当然也不排除某天我改主意了。未来额外的内容也可能另起一章加到目录索引中。
在“最后”一篇, 我想我会讲一些随机曲线,这些曲线不值得单独开一章来讲。还有,我觉得把我从找到公式到编码的过程完整过一遍会很不错。

Weisstein, Eric W "大麻曲线" 来源于网站 https://mathworld.wolfram.com/CannabisCurve.html
Wolfram Mathworld 是一个很好的发掘有趣公式的地方,顺便说一句,如果你想发掘更多 2d 曲线,那么在平面曲线(Plane Curve)这一章节可以深入找找。网站内容很全,还有其它曲线类型可探索。
为什么选择大麻曲线?。我只是觉得它很酷(译者注:本人在此申明我与赌毒不共戴天),仅仅用简单的相关地数学公式就可以画出如此复杂的东西。
下面是对应的数学公式:
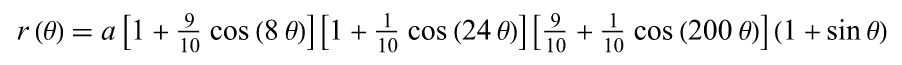
好的,公式有点儿长,但它只是乘法,加法还有一些正弦和余弦计算。我们可以的。
它定义了一条极坐标曲线,这意味着相比于 x, y 的值,我们更关心角度与半径。我们有个函数 r(θ), θ 是希腊字母,theta。它通常代表角度。当然我们也能猜到 r 代表半径。所以我们需要一个函数传入角度得到对应的半径。
有了角度和半径,我们很容易计算出用于绘制线段的 x,y 点。组织代码后应该像下面在这样:
for (t = 0; t < 2 * PI; t += 0.01) {
radius = r(t)
x = cos(t) * radius
y = sin(t) * radius
lineTo(x, y)
}
stroke()
我们通过 t 计算得到半径,然后再通过半径和 t 计算得到下一个绘制线条的坐标点。
不过事实上来讲,r(θ) 除了在这个循环内不会在其它任何地方使用,我就直接硬编码了。
此处唯一额外要说明的就是需要传入参数 radius 用 radius 乘以公式。还需要用 x, y 让曲线居于中心点,所以我们也把它作为参数传递(xc 与 yc 代表 x 和 y 中点)。
(译者注:这里原作都在 r(t) 计算时用字母小 a 指代除公式之外的部分, 我觉得更难理解更麻烦,小 a 在英语中随处可见,又不在伪代码中明确标出,所以我决定去掉。直接用中文表达出作者原本的意图)
以下面代码作为起点:
function cannabis(xc, yc, radius) {
for (t = 0; t < 2 * PI; t += 0.01) {
r = radius * ... // that whole formula. we'll get to it.
x = cos(t) * r
y = sin(t) * r
lineTo(xc + x, yc + y)
}
closePath()
}
现在,我们在上面基础上进行编码。相当的简单,我们只需代入公式。分数部分我们使用 0.1 代替 1/10, 0.9 代替 9/10。开始吧!
function cannabis(xc, yc, radius) {
for (t = 0; t < 2 * PI; t += 0.01) {
r = radius * (1 + 0.9 * cos(8 * t)) * (1 + 0.1 * cos(24 * t)) * (0.9 + 0.1 * cos(200 * t)) * (1 + sin(t))
x = cos(t) * r
y = sin(t) * r
lineTo(xc + x, yc + y)
}
closePath()
}
现在,像下面代码这样看看:
canvas(600, 600)
cannabis(300, 300, 140)
stroke()
That gives me this image:
这会得到如下图:
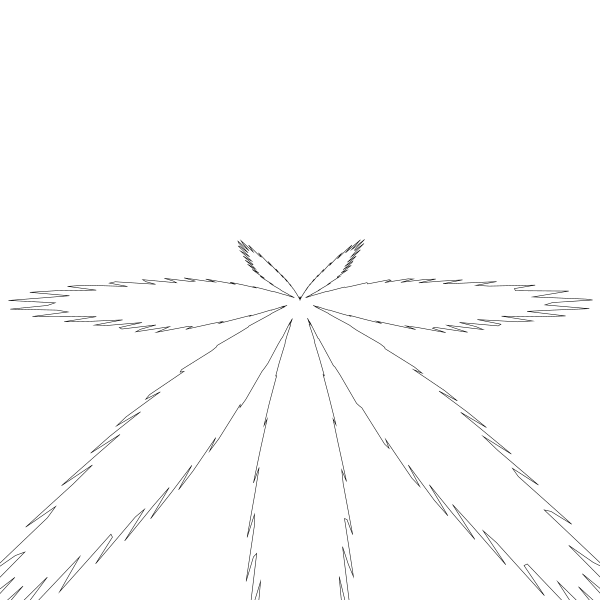
Ah, 好的,有点儿东西。
首先,此公式使用笛卡尔坐标系,而我用的是上下相反的屏幕坐标系。所以我需要把 y 轴翻转。问题不大。
接着,中心点是所有“叶子”连接点。所以在翻转后,我可以将中心点设置在 canvas 靠近底部的位置。
最后,我猜 140 会是一个不错的半径值,它会将绘制出的图形限制在 600X600 大小的 canvas 内。事实上,我期望的是把图形限制在 canvas 大小的一半。但实际上大的叶子超出一部分也不影响。我们可以在代码中修复它,比如将半径乘以某些小数让大的叶子半径降下来。我就不做这部分限制了,我假装自己只会传合适的值,相关限制代码你自己可以搞定的。
function cannabis(xc, yc, radius) {
for (t = 0; t < 2 * PI; t += 0.01) {
r = radius * (1 + 0.9 * cos(8 * t)) * (1 + 0.1 * cos(24 * t)) * (0.9 + 0.1 * cos(200 * t)) * (1 + sin(t))
x = cos(t) * r
y = sin(t) * r
lineTo(xc + x, yc - y)
}
closePath()
}
我所做的只是将 lineTo 这一行用yc + y 代替了 yc - y 。
在调用函数时参数也调整了一下(经过试错后得出还不错的参数值)
canvas(600, 600)
cannabis(300, 520, 120)
stroke()
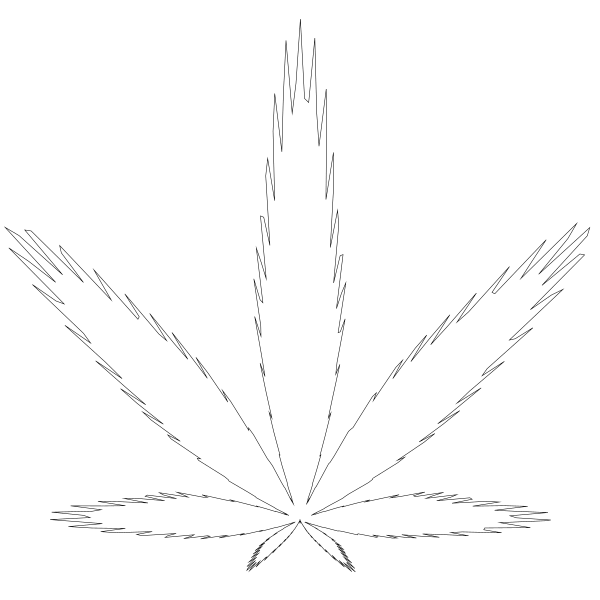
结果还阔以!
提醒一下。我经过仔细考虑调整了 canvas 的大小,这样 yc 参数值可以设置到 420。 你调不调的隨你🙂。
当然,现在我很好奇这个公式到底做了些什么。 radius * 后面分 4 部分,圆括号内分别有 -- 三个 余弦 cos, 一个正弦 sin。第一个括号内直接写了数值(硬编码) 8 。
... (1 + 0.9 * cos(8 * t)) ...
自从设了值为 8 便有了 7 片可见的叶子,我猜它们之间有联系 - 它实际上有可能有 8 片叶子,只是最底部的那一片太小,我们看不到。 我将 8 调高到 12 ...
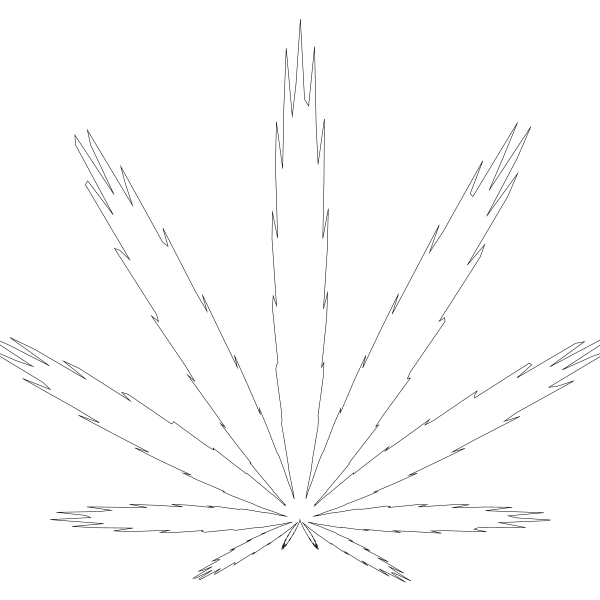
你看看!理论验证成功。 7 片可见叶子加上一片不可见的。
在第二部分数 24 的作用就不太容易看出来。
... (1 + 0.1 * cos(24 * t)) ...
如果把代码回调然后把数值 24 设为 0 ,叶子边缘会非常圆润。
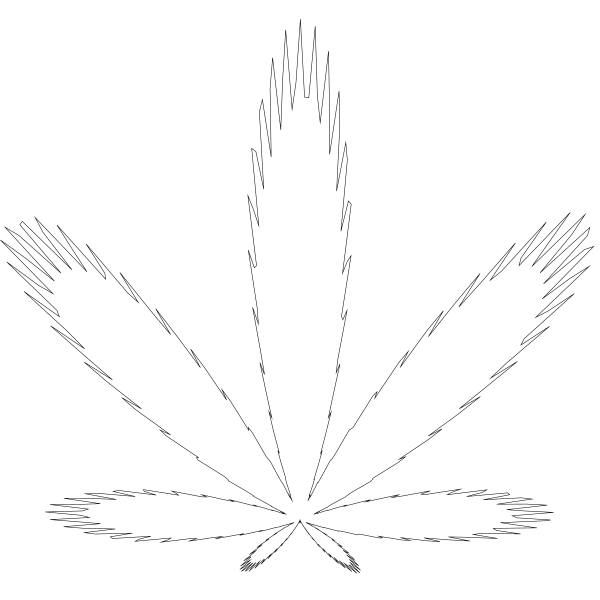
调到 24 一倍至 48 会得到:
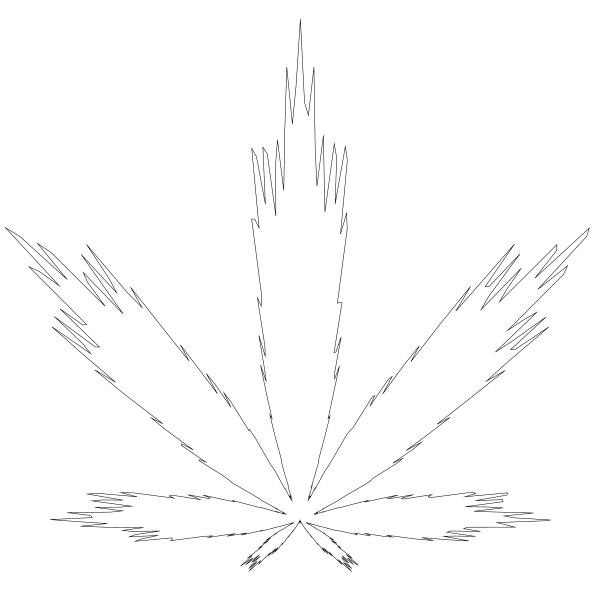
这结果有点儿像每片叶子上又生出了三片小叶子。让我们把值改回 24 然后改变乘数:
... (0.7 + 0.3 * cos(24 * t)) ...
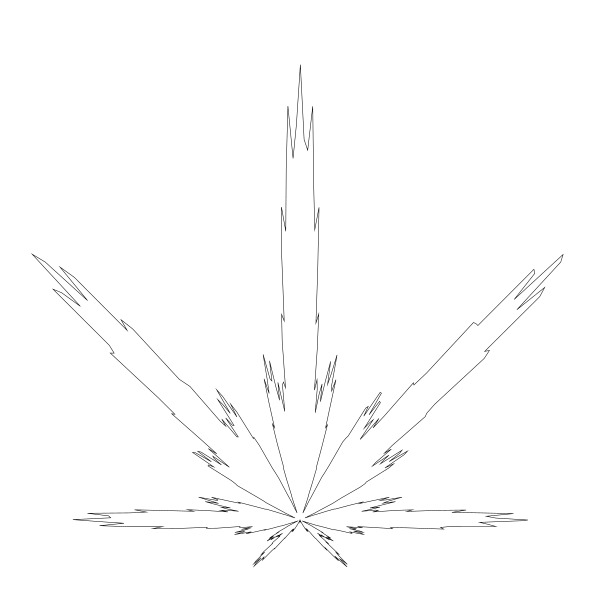
还是看到三片小叶子,24 = 8 * 3 很合理。所以这部分使用非常小的乘数, 0.1, 来微调每片叶子 - 让它变的不那么圆润。酷。把代码调回原位后再往下看另一部分。
... (0.9 + 0.1 * cos(200 * t)) ...
数值 200 我猜是用来创建锯齿边的。如果我把它 改为 100 , 锯齿变就变少了。
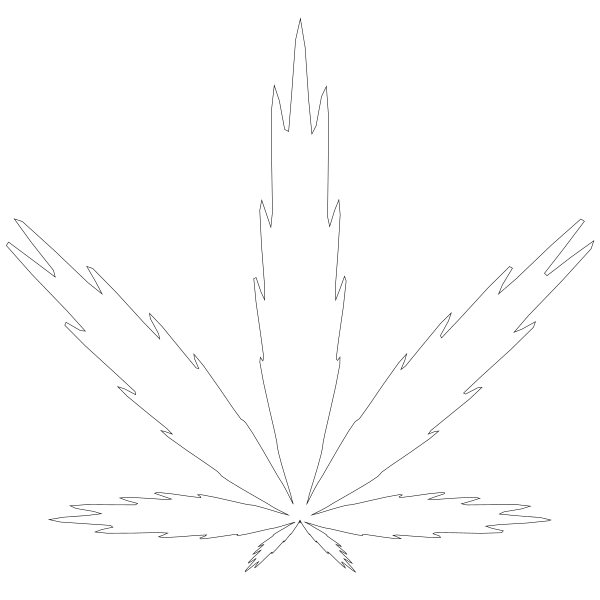
但现在看起来块儿状化了。试着增加分辨率把 for 循环从 0.01 调至 0.005:
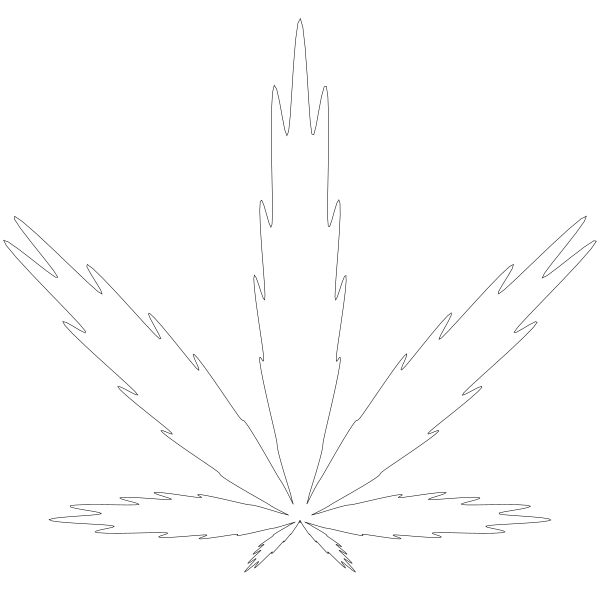
Mmmm... 丝滑。
反代码复原后再看最后一个 sin 的作用。
... (1 + sin(t))
我一开始猜它影响的是曲线的朝向。我想如果把这部分删掉,叶子可能会朝向一边。但我发现我猜错了。下面是我移掉这部分代码并将 yc 调回到 canvas 中心点 300 后的结果:
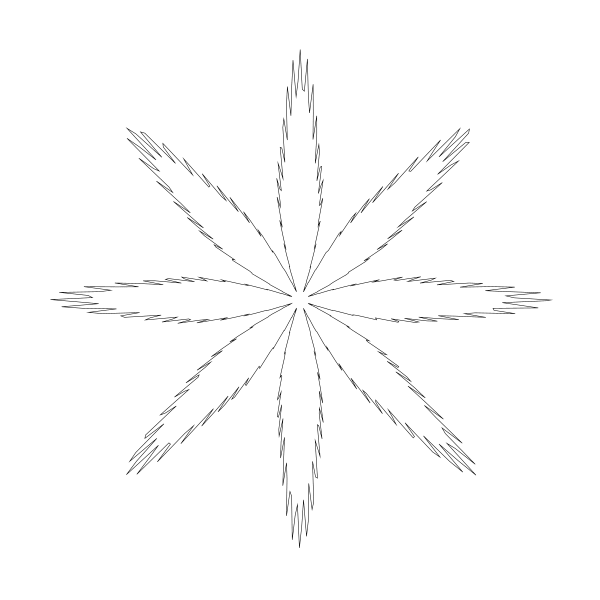
真是个小惊喜!在这个基础上我的点子可就多了,另外那消失的第 8 片叶子也找到了!
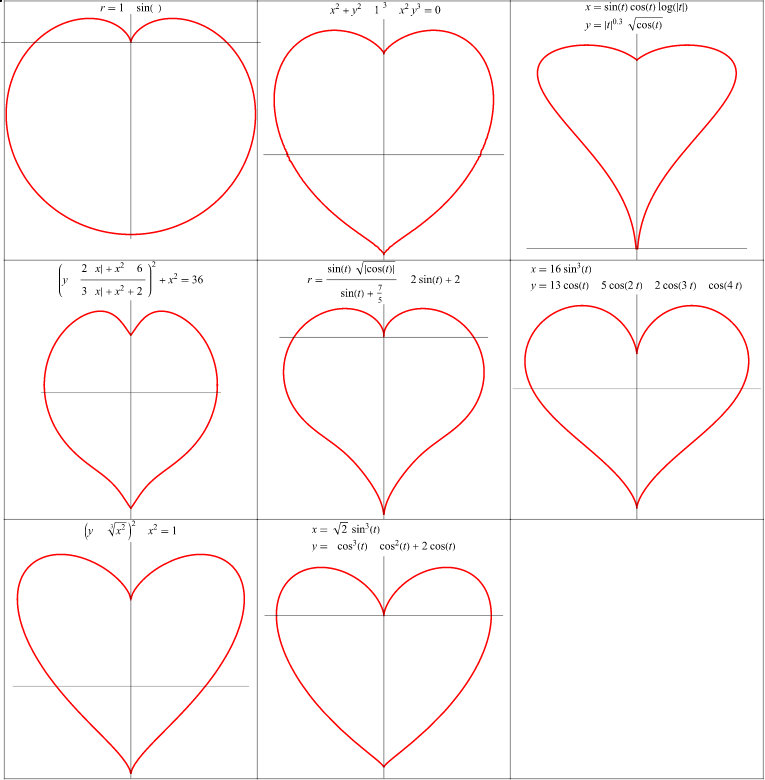
Weisstein, Eric W. “Heart Curve.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/HeartCurve.html
再一次,还得靠 Mathworld。如你所见,没有一个单独的公式可以绘制心形曲线。此页展示了 8 种不同的绘制方法。个人来讲我喜欢倒数第二行的最后一个。
相比于上一次接触的极坐标公式(还有其中其它的例子), 此公式直接给出计算 x 和 y 值。当然还是得用 0 到 2*PI 循环出 t 值。
公式计算 y 坐标,有四个不同的计算部分。不太清楚四个计算合在一起的作用,但如果往下继续看,你会想着删减它们。我关心的还有两点,硬编码的数值太多还有就是没有直接改变心形大小的参数。但我肯定我们可以解决。
来吧,这是非常直接的公式,我们直接进入代码环节用代码写出来。
function heart(xc, yc) {
for (t = 0; t < 2 * PI; t += 0.01) {
x = 16 * pow(sin(t), 3)
y = 13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t)
lineTo(xc + x, yc + y)
}
closePath()
}
We can run this like so:
像下面这样调用:
canvas(600, 600)
heart(300, 300)
stroke()
And we’ll get:
得到结果:

基本正确,只是需要把它翻转过来,还有就是需要允许调整大小。现在大约宽度是 32 像素。这是硬编码值 16,乘以 2 倍。
翻转就很简单了再次将使用 yc - y
至于尺寸大小,先把硬编码的数值分别除以 16。
x = pow(sin(t), 3)
y = 0.8125 * cos(t) - 0.3125 * cos(2 * t) - 0.125 * cos(3 * t) - 0.0625 * cos(4 * t)
像这样处理后,我们得到的是 2 像素宽度的(1 * 2)心形(译都注:x 轴系数16/16归 1 了,原来 16 是 32 像素意味着输出的图像 1 就是 2 像素)。现在我们可以为它添加控制大小参数 size 了。
function heart(xc, yc, size) {
for (t = 0; t < 2 * PI; t += 0.01) {
x = size * pow(sin(t), 3)
y = size * (0.8125 * cos(t) - 0.3125 * cos(2 * t) - 0.125 * cos(3 * t) - 0.0625 * cos(4 * t))
lineTo(xc + x, yc - y)
}
closePath()
}
现在像下面这样调用:
canvas(600, 600)
heart(300, 300, 280)
stroke()
得到的结果:
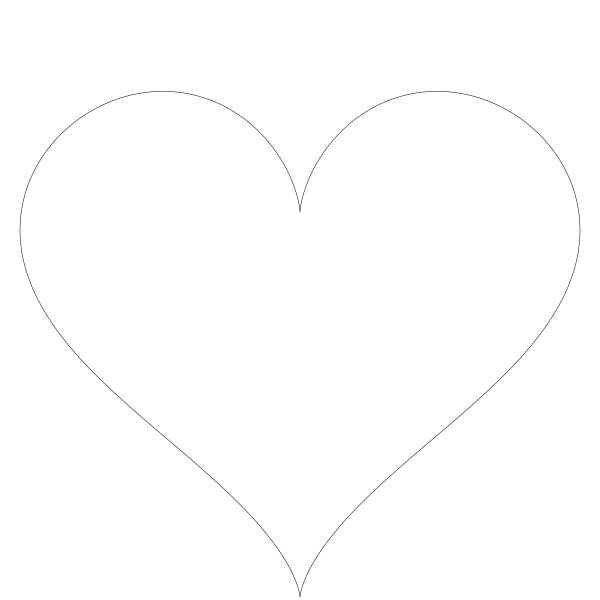
不是很难。
我不打算再深入另外的心形的公式了,相信你自己可以探索,你只需改动其中的常数值看看会发生什么变化。你有更好的方式吗?完全不同的那种?
蛋(卵形)
几年前我才首次接触如何绘制蛋形。此篇中只展示结果,但没有写思考过程。这篇比较完整 https://www.bit-101.com/blog/2021/06/how-to-draw-an-egg/
公式是从这里找到的 http://www.mathematische-basteleien.de/eggcurves.htm
事实上这里有超多的绘制蛋形的公式。就像心形曲线一样,我好奇的是没有一个单独的绘制蛋形曲线的标准公式。
但我把目标锁定在了 “From the Oval to the Egg Shape” 这一章节。此处有一个通用的蛋形或椭圆形公式,y 轴半径在每个点上都是变化的。如果 x 偏右,则 y 值变大,如果 x 偏左则 y 值编小。很直观。
所以我们先从椭圆公式开始,椭圆公式在第三章中我们已经讲解过了。
function ellipse(x, y, rx, ry) {
res = 4.0 / max(rx, ry)
for (t = 0; t < 2 * PI; t += res) {
lineTo(x + cos(t) * rx, y + sin(t) * ry)
}
closePath()
}
公式很好很简洁,但我得把三角函数部分代码提出来方便对它进行平衡与缩放。为了简洁的解释我还把 res 变量去掉了直接硬编码为 0.01, 当然你可以选择保留它。
function egg(xc, yc, rx, ry) {
for (t = 0; t < 2 * PI; t += 0.01) {
x = cos(t)
y = sin(t)
lineTo(xc + x * rx, yc + y * ry)
}
closePath()
}
就是画了个椭圆,只是先确定改动代码有没有错误。
canvas(600, 600)
egg(300, 300, 280, 190)
stroke()

Yup,结果正是个椭圆。数值 280 和 190 是怎么来的?嗯,280 就是比 canvas 宽度一半还小一点点,rx。 ry 也是类似,不断试错后得到 190 这个看起来不错的值。
现在让我们把椭圆变成蛋形。那个网页中给了我们三个公式:
t1(x) = 1 + 0.2 * x
t2(x) = 1 / (1 - 0.2 * x)
t3(x) = e^(0.2 * x)
这些 t 函数是用来乘以 y 的。我就不再创建新函数了。就在 for 循环中直接乘。先从第一个 t 公式开始...
function egg(xc, yc, rx, ry) {
for (t = 0; t < 2 * PI; t += 0.01) {
x = cos(t)
y = sin(t)
y *= (1 + 0.2 * x)
lineTo(xc + x * rx, yc + y * ry)
}
closePath()
}

Woo! 得到了一个蛋!
现在我们可以调调公式内的参数了。先从 0.2 这个数值入手。把它设为 0.3 试试。

好的,它看起变的有点儿尖。改为 0.5?

更尖了。懂了哈。把值改回 0.1。
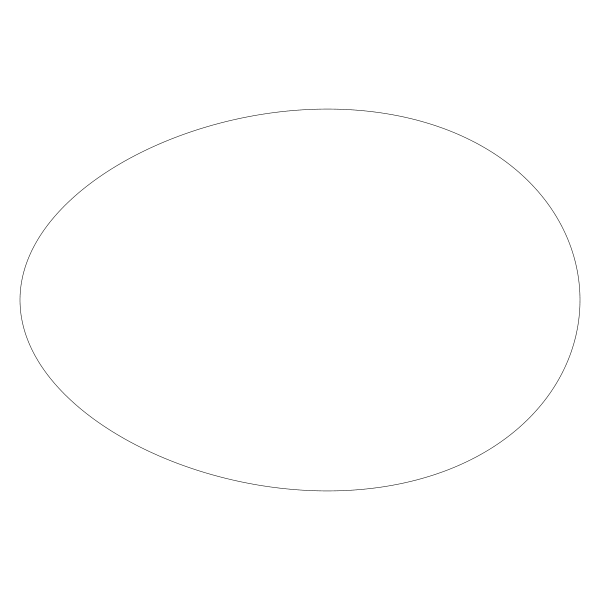
几乎与原椭圆别无二至。这说得通,如果值为 0, 那么这一行啥也没做,它就是个椭圆。让我们把它改回 0.2, 让它变成通常常见的蛋型,再把 ry 改成 220:

一个漂亮“肥”蛋。下面是 150:

我坚持我的数值 190 ,但小调一点也可能更好。多试试吧。让我们再试试其它公式。首先把 ry 调回 190。把公式换成:
y *= 1 / (1 - 0.2*x)

再试试第三个公式
y *= exp(0.2 * x)
还记得第五章提到过大部分数学库都会提供 exp 函数即 e^x ( e 的“参数”次幂)。这个公式就是调用了 exp 函数,结果如:

由于三个公式看起来都很像,所以我把它们用红绿蓝三种不同颜色都画了出来...

Yeah, 三个几乎相同。可能有几个像素的区别。让我们回头看原网站,它们讨论的是另一种不同的椭圆公式,并且让 y2 乘以 此公式的值:
另一种椭圆公式 x²/9+y²/4=1 变化至 x²/9+y²/4*t(x)=1
除数 9 和 4 依然是硬编码。如果对它们开方得到 3 和 2。而 280 的 2/3 刚好是 186(译者注:公式简化后可观察得到 ry 是 2/3 的 rx)。 所以之前我选择 ry 为 190 挺合理的!
无论如何,我们有了可以画出令人信服的蛋形公式,无论使用哪种算法。就到这儿吧。这就是我写文章的过程,当然我写代码也是类似的思考,你完整的了解了整个过程,去掉了一些源文中的细枝末节。但得到的结果依然相当不错!
(译者注:很多情况下你不需要知道公式的完整推导过程,人生苦短直接使用公式即可)
如何从不同地方找到各种公式把它们转变成代码绘制出有趣的图形, 希望这会给你一些启发 - 如果你从未做过的话。
我把它们全部归档到了 coding curves 系列中。至少现在为止是这样。不过我想到了另一个系列,关注我不迷路!
博客园: http://cnblogs.com/willian/
github: https://github.com/willian12345/
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK