NCERT Solutions Class 10 Maths Chapter 8 Introduction to Trigonometry resource was developed by GFG experts to aid students in answering questions they may have as they go through problems from the NCERT textbook. All of the problems in this chapter’s exercise from the NCERT textbook are covered in the NCERT Solutions for Class 10 Maths.

The ratio of every right-angled triangle’s sharp angles to its right angles is examined in the chapter Introduction to Trigonometry. The trigonometric ratios of particular angles, trigonometric identities, and trigonometric ratios of complementary angles are the foundations for the chapter’s problems.

These Solutions cover all the exercises of the NCERT Class 10 Maths Chapter 8, which are as follows:

Class 10 Maths NCERT Solutions Chapter 8 Exercises
NCERT Maths Solutions Class 10 Exercise 8.1 – 11 Questions (8 Short Answers, 3 Long Answers)
NCERT Maths Solutions Class 10 Exercise 8.2– 4 Questions (2 Short Answers, 2 Long Answers)
NCERT Maths Solutions Class 10 Exercise 8.3 – 7 Questions (5 Short Answers, 2 Long Answers)
NCERT Maths Solutions Class 10 Exercise 8.4 – 5 Questions (3 Short Answers, 2 Long Answers)

Introduction to Trigonometry: Exercise 8.1

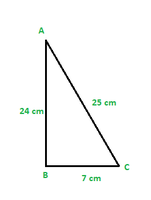
Question 1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:

(i) sin A, cos A (ii) sin C, cos C

Solution:

Using Pythagoras theorem for ΔABC

AC2 = AB2 + BC2

= (24 cm)2 + (7 cm)2

= (576 + 49) cm2

= 625 cm2

∴AC = 25 cm       

(i) sin A = opp/hyp

    sin A = 7/25

    cos A = adj/hyp = 24/25

    cos A = 24/25

(ii) sin C = opp/hyp

     sin C = 24/25

     cos C = adj/hyp

     cos C = 7/25

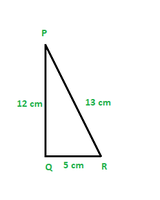
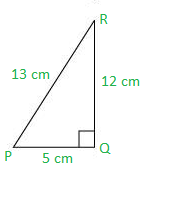
Question 2. In Fig., find tan P – cot R.

Solution:

Applying Pythagoras theorem for ΔPQR, we obtain

PR2 = PQ2 + QR2

(13 cm)2 = (12 cm)2 + QR2

169 cm2 = 144 cm2 + QR2

25 cm2 = QR2

QR = 5 cm

tan P = opp/adj

tan P = 5/12

cot R = adj/opp

cot R = 5/12

tan P – cot R = 5/12 – 5/12 = 0

Question 3. If sin A = 3/4, calculate cos A and tan A.

Solution:

Using sin2A + cos2A = 1

(3/4)2 + cos2A = 1

cos2A = 1 – (3/4)2 = 1 – 9/16

cos A = 71/2/4

tan A = sin A/cos A

tan A = (3/4)/(71/2/4)

tan A = 3/71/2

Question 4: Given 15 cot A = 8. Find sin A and sec A

Solution:

Given, 15 cot A = 8

               cot A = 8/15

tan A = 1/cot A

tan A = 15/8

Using, 1 + tan2A = sec2A

           1 + (15/8)2 = sec2A

           289/64 = sec2A

           sec A = 17/8 

We know, cos2A = 1/sec2A

                cos2A = 64/289

               sin2A = 1 – cos2A

               sin2A = 225/289

              sin A = 15/17

Question 5: Given sec θ = 13/12, calculate all other trigonometric ratios.

Solution.

Using Pythagoras theorem,

sin θ = 5/13

cos θ = 12/13

tan θ = 5/12

cosec θ = 13/5

cot θ = 12/5

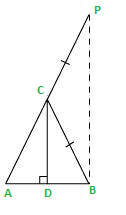
Question 6: If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Solution:

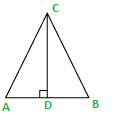
Let us consider a ΔABC in which CD ⊥ AB.

It is given that cos A = cos B

AD/AC = BD/BC     … (1)

We need to prove ∠A = ∠B. To prove this, we need to extend AC to P such that BC = CP.

From equation (1), we obtain

AD/BD = AC/BC

AD/BD = AC/CP    (BC = CP by construction)

By using the converse of B.P.T (Basic Proportionality Theorem),

CD||BP

∠ACD = ∠CPB (Corresponding angles) … (3)

And, ∠BCD = ∠CBP (Alternate interior angles) … (4)

By construction, we have BC = CP.

∴ ∠CBP = ∠CPB (Angle opposite to equal sides of a triangle) … (5)

From equations (3), (4), and (5), we obtain

∠ACD = ∠BCD … (6)

In ΔCAD and ΔCBD,

∠ACD = ∠BCD (Using equation (6))

∠CDA = ∠CDB (Both 90°)

Therefore, the remaining angles should be equal.

∴∠CAD = ∠CBD

⇒ ∠A = ∠B

Question 7: If cot θ = 7/8, evaluate

(i) ((1 + sinθ) * (1 – sinθ))/(1 + cosθ) * (1 – cosθ)))

(ii) cot2θ

Solution:

(i) Using (a + b) * (a – b) = a2 – b2 in numerator and denominator

We get

(1 – sin2θ)/(1 – cos2θ)

Using sin2θ + cos2θ = 1

We get

cos2θ/sin2θ = cot2θ

cot2θ = (7/8)2 = 49/64

(ii) cot2θ = (7/8)2 = 49/64

Question 8. If 3 cot A = 4, Check whether (1 – tan2A)/(1 + tan2A) = cos2A – sin2A

Solution.

We know that, tanA = sinA / cosA   ….(1)

Using (1) on L.H.S

= (1 – sin2A/cos2A)/(1 + sin2A/cos2A)

which on rearranging becomes

= (cos2A – sin2A)/(cos2A + sin2A)

Using the identity,

cos2A + sin2A = 1

LHS becomes

= (cos2A – sin2A)

This is equal to RHS.

LHS = RHS (for every value of cot A)

Hence, Proved.

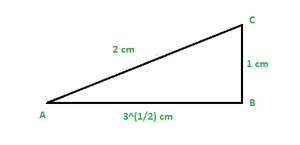
Question 9: In ΔABC, right-angled at B. If tan A = 1/(31/2), find the value of

(i) sin A cos C + cos A sin C

(ii) cos A cos C − sin A sin C

Solution:

Using Pythagoras theorem

(AB)2 + (BC)2 = (AC)2

(31/2)2 + (1)2 = (AC)2

which gives

AC = 2 cm

Using formulas

sin A = 1/2

sin C = 31/2/2

cos A = 31/2/2

cos C = 1/2

Now, (i) sin A cos C + cos A sin C

Substituting the values

= (1/2) * (1/2) + (31/2/2) * (31/2/2)

= 1/4 + 3/4

= 1

Now, (ii) cos A cos C − sin A sin C

Substituting the values

= (31/2/2) * (1/2) – (1/2) * (31/2/2)

= 31/2/4 – 31/2/4

= 0

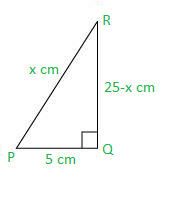
Question 10: In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P, and tan P.

Solution:

Given that, PR + QR = 25

Let PR be x cm.

Therefore, QR = 25 − x cm

Applying Pythagoras theorem in ΔPQR, we obtain

PR2 = PQ2 + QR2

x2 = (5)2 + (25 − x)2

x2 = 25 + 625 + x2 − 50x

50x = 650

Therefore, PR = 13 cm

QR = (25 − 13) cm = 12 cm

sin P = QR/PR = 12/13

cos P = PQ/PR = 5/13

tan P = QR/PQ = 12/5

Question 11. State whether the following are true or false. Justify your answer.

(i) The value of tan P is always less than 1.

(ii) sec A = 12/5 for some value of angle A.

(iii) cos A is the abbreviation used for the cosecant of angle A.

(iv) cot A is the product of cot and A

(v) sin θ = 4/3, for some angle θ

Solution:

(i) Consider a ΔPQR, right-angled at Q as shown below.

Here tan P = 12/5 which is surely greater than 1.

Therefore, the statement is false.

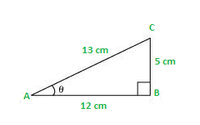
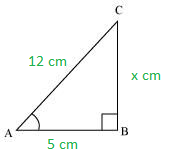
(ii) Consider ΔABC with AB = 5 cm, AC = 12 cm and BC = x cm

Using Pythagoras theorem in ΔABC

(AB)2 + (BC)2 = (AC)2

52 + x2 = 122

x = (144 – 25)1/2

x = (119)1/2

x = 10.9 cm

AB < BC < AC

So this triangle is valid,

Therefore, given statement is true.

(iii) Abbreviation used for cosecant A is cosec A. And cos A is the abbreviation used for cosine A.

Hence, the given statement is false.

(iv) cot A is not the product of cot and A. It is the cotangent of ∠A.

Hence, the given statement is false.

(v) sin θ = 4/3 

In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of sin θ is not possible.

Hence, the given statement is false

Introduction to Trigonometry: Exercise 8.2

Question 1. Evaluate the following : 

(i) sin 60° cos 30° + sin 30° cos 60° 

Solution:

Formulas to be used : sin 30° = 1/2

                                      cos 30° = √3/2

                                      sin 60° = 3/2

                                      cos 60° = 1/2

=> (√3/2) * (√3/2) + (1/2) * (1/2)

=> 3/4 +1/4

=> 4 /4 

=> 1

(ii) 2 tan245° + cos230° – sin260°

Solution:

Formulas to be used : sin 60° = √3/2

                                     cos 30° = √3/2

                                     tan 45° = 1

 => 2(1)(1) + (√3/2)(√3/2)-(√3/2)(√3/2)

 => 2 + 3/4 – 3/4

 => 2

(iii) cos 45°/(sec 30°+cosec 30°)

Solution: 

Formulas to be used : cos 45° = 1/√2

                                      sec 30° = 2/√3

                                      cosec 30° = 2

=> 1/√2 / (2/√3 + 2)

=> 1/√2 / (2+2√3)/√3   

=> √3/√2×(2+2 √3) = √3/(2√2+2√6)

=> √3(2√6-2√2)/(2√6+2√2)(2√6-2√2)

=> 2√3(√6-√2) / (2√6)²-(2√2)²

=> 2√3(√6-√2)/(24-8) = 2 √3(√6-√2)/16 

=> √3(√6-√2)/8

=> (√18-√6)/8  

=> (3√2-√6)/8

(iv) (sin 30° + tan 45º – cosec 60°)/(sec 30° + cos 60° + cot 45°)

Solution: 

Formulas to be used : sin 30° = 1/2

                                     tan 45° = 1

                                     cosec 60° = 2/√3

                                     sec 30° = 2/√3

                                     cos 60° = 1/2

                                     cot 45° = 1

=> (1/2+1-2/√3) / (2/√3+1/2+1)

=> (3/2-2/√3)/(3/2+2/√3)

=> (3√3-4/2 √3)/(3√3+4/2 √3)

=> (3√3-4)(3√3-4)/(3√3+4)(3√3-4)

=> (27+16-24√3) / (27-16)

=> (43-24√3)/11

(v) (5cos260° + 4sec2 30° – tan245°)/(sin230° + cos²30°)       

Solution:

Formulas to be used : cos 60° = 1/2

                                      sec 30° = 2/√3

                                      tan 45° = 1

                                      sin 30° = 1/2

                                      cos 30° = √3/2

=> 5(1/2)2+4(2/√3)²-1²/(1/2)+(√3/2)

=> (5/4+16/3-1) / (1/4+3/4)

=> (15+64-12) / 12/(4/4)

=> 67/12

Question 2. Choose the correct option and justify your choice:

(i) 2tan 30°/1+tan230° =

(A) sin 60°            (B) cos 60°          (C) tan 60°            (D) sin 30°

(ii) 1-tan245°/1+tan245° =

(A) tan 90°            (B) 1                    (C) sin 45°            (D) 0

(iii)  sin 2A = 2 sin A is true when A =

(A) 0°                   (B) 30°                  (C) 45°                 (D) 60°

(iv) 2tan30°/1-tan230° =

(A) cos 60°          (B) sin 60°             (C) tan 60°           (D) sin 30°

Solution: 

(i) In the given equation, substituting the value of tan 30° 

As tan 30° = 1/√3

2tan 30°/1+tan230° = 2(1/√3)/1+(1/√3)2

=> (2/√3)/(1+1/3) = (2/√3)/(4/3)

=> 6/4√3 = √3/2 

=> sin 60°   

The ans is sin 60°. 

The correct option is (A).

(ii) In the given equation, substituting the of tan 45° 

 As tan 45° = 1

1-tan245°/1+tan245° = (1-12)/(1+12)

= 0/2 => 0

The ans is 0. 

The correct option is (D).

(iii) sin 2A = 2 sin A is true when A = 0°

sin 2A = sin 0° = 0

 2 sin A = 2 sin 0° = 2 × 0 = 0

 Another way :

 sin 2A = 2sin A cos A

=> 2sin A cos A = 2 sin A

=> 2cos A = 2 => cos A = 1

Now, we have to check which degree value has to be applied, to get the solution as 1.

When 0 degree is applied to cos value we get 1, i.e., cos 0 = 1

Hence, A = 0°

The correct option is (A).

(iv) As tan 30° = 1/√3

2tan30°/1-tan230° =  2(1/√3)/1-(1/√3)2

=> (2/√3)/(1-1/3) = (2/√3)/(2/3) = √3 = tan 60°

The correct option is (C).

Question 3. If tan (A + B) = √3 and tan (A – B) = 1/√3, 0° < A + B ≤ 90°; A > B, find A and B.

Solution: 

tan (A + B) = √3 

tan (A + B) = tan 60°

(A + B) = 60° … (i)

tan (A – B) = 1/√3

tan (A – B) = tan 30°

(A – B) = 30° …  (ii)

Now add the equation (i) and (ii), we get

A + B + A – B = 60° + 30°

A= 45°

Substituting the value of A in equation (i) to find the value of B

45° + B = 60°

B = 60° – 45°   

 B = 15°

Hence, A = 45° and B = 15°

Question 4. State whether the following are true or false. Justify your answer.

(i) sin (A + B) = sin A + sin B.

(ii) The value of sin θ increases as θ increases.

(iii) The value of cos θ increases as θ increases.

(iv) sin θ = cos θ for all values of θ.

(v) cot A is not defined for A = 0°.

Solution: 

(i) Let us take A = 60° and B = 30°, then

Substitute the values of A and B in the sin (A + B) formula, we get

sin (A + B) = sin (60° + 30°) = sin 90° = 1 and,

sin A + sin B = sin 60° + sin 30°

= √3/2 + 1/2 = (√3 + 1 ) / 2, sin(A + B) ≠ sin A + sin B 

Since both the values obtained are not equal. 

Hence, the statement is false.

(ii) From the values given below, we can see that as angle(theta) increases value also increases.

sin 0° = 0, sin 30° = 1/2, sin 45° = 1/√2, sin 60° = √3/2 , sin 90° = 1

Thus, the value of sin θ increases as θ increases.

Hence, the statement is true. 

(iii) From the values given below, we can see that as angle (theta) increases value decreases.

cos 0° = 1, cos 30° = √3/2 , cos 45° = 1/√2, cos 60° = 1/2, cos 90° = 0

Thus, the value of cos θ decreases as θ increases. 

Hence, the statement given above is false.

(iv) sin θ = cos θ, is only true for theta = 45° 

Therefore, the above statement is false.

(v) As tan 0° = 0

cot 0° = 1 / tan 0° 

= 1 / 0 => undefined

Hence, the given statement is true.

Introduction to Trigonometry: Exercise 8.3

Question 1. Evaluate:

(i) sin 18° / cos 72°

Solution:

Since, 

cos 72°  = cos ( 90° – 18° ) = sin 18°

Therefore, 

sin 18° / cos 72° = sin 18° / sin 18°  = 1

Hence, sin 18° / cos 72°  = 1.

(ii) tan 26° / cot 64°

Solution:

Since,

cot 64°  = cot ( 90° – 26° ) = tan 26°

Therefore,

tan 26° / cot 64° = tan 26° /  tan 26°  = 1

Hence, tan 26° / cot 64°  = 1.

(iii) cos 48° – sin 42°

Since,

cos 48°  = cos ( 90° – 42° ) = sin 42°

Therefore,

cos 48° – sin 42° = sin 42° –  sin 42°  = 0

Hence, cos 48° – sin 42°  = 0.

(iv) cosec 31° – sec 59°

Solution:

Since,

sec 59°  = sec ( 90° – 31° ) = cosec 31°

Therefore ,

cosec 31° – sec 59° = cosec 31° – cosec 31°  = 0

Hence, cosec 31° – sec 59°  = 0.

Question 2. Show that:

(i) tan 48° tan 23° tan 42° tan 67° = 1

Solution:

Let A = tan 48° tan 23° tan 42° tan 67°

Since ,

tan 23° = tan( 90° – 23° ) = cot 67° and,

tan  42° = cot(  90° –  42° ) = cot  48°

Therefore,

A = tan 48° cot 67° cot  48° tan  67°

A = 1  (Since, tan B° cot  B° = 1)

Hence, tan 48° tan 23° tan 42° tan 67° = 1

 (ii) cos 38° cos 52° – sin 38° sin 52° = 0

Let A = cos 38° cos 52° – sin 38° sin 52°

Since,

sin 52° = sin (90° – 38°) = cos 38° and,

cos  52° = cos(90° –  52°) = sin 38°

Therefore,

A = cos 38° sin 38° – sin 38° cos 38°

Hence, cos 38° cos 52° – sin 38° sin 52° = 0.

Question 3. If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.

Solution:

We have, 

tan 2A = cot ( A – 18° )  —(1)

Since,

tan (2A) = cot ( 90° – 2A )  — (2)

Putting (2) in (1),

cot ( 90° – 2A ) = cot ( A – 18° ) 

Therefore,

90° – 2A = A – 18°

3A = 108°

A = 36°

Hence, A = 36°.

Question 4. If tan A = cot B, prove that A + B = 90°. 

Solution:

We have,

tan A = cot B —(1)

Since,

tan (A) = cot (90° – A)  — (2)

Putting (2) in (1),

cot (90° – A) = cot (B)

Therefore,

90° – A = B

Hence, A + B = 90°.

Question 5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.

Solution:

We have,

sec 4A = cosec ( A – 20° )  —(1)

Since,

sec 4A = cosec ( 90° – 4A )  — (2)

Putting (2) in (1),

cosec ( 90° – 4A ) = cosec ( A  – 20° )

Therefore,

90° – 4A = A – 20°

5A = 110°

A = 22°

Hence, A = 22°.

Question 6. If A, B, and C are interior angles of a triangle ABC, then show that  sin ((B + C) / 2) = cos (A / 2).

Solution:

Let T = sin ((B + C) / 2) — (1)

A, B and C are the interior angles of triangle ABC, therefore,

A + B + C = 180° 

Dividing by 2 on both sides

(B + C)/2  = 90° – (A / 2) —(2)

Putting (2) on (1)

T = sin (90° – (A / 2) 

   = cos (A / 2)

Hence, sin ((B + C)/2) = cos (A / 2).

Question 7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°

Solution:

Let A = sin 67° + cos 75°

Since,

sin 67° = sin(90° – 23°) = cos (23°)

cos 75° = cos (90° – 15°) = sin (15°)

Therefore,

sin 67° + cos 75° = cos 23° + sin 15°

Introduction to Trigonometry: Exercise 8.4

Question 1. Express the trigonometric ratios sin A, sec A, and tan A in terms of cot A

Solution:

(i) sin A

We know that

cosec2A = 1 + cot2A

1/sin2A = 1 + cot2A

sin2A = 1/(1 + cot2A)

sin A = 1/(1+cot2A)1/2

(ii) sec A 

sec2A = 1 + tan2A

Sec2A = 1 + 1/cot2A

sec2A = (cot2A + 1) / cot2A

sec A = (cot2A + 1)1/2 / cot A

(iii) tan A

tan A = 1 / cot A

tan A = cot -1 A

Question 2. Write all the other trigonometric ratios of ∠A in terms of sec A.

Solution:

(i) cos A

cos A = 1/sec A

(ii) sin A

We know that

sin2A = 1 – cos2A

Also , cos2A = 1 / sec2A

sin2A = 1 – 1 / sec2A

sin2A = (sec2A – 1) / sec2A

sin A = (sec2A – 1)1/2 / sec A

(iii) tan A

We know that

tan2A + 1 = sec2A

tan A = (sec2A – 1)½

(iv) cosec A

We know

cosec A = 1/ sinA

cosec A = sec A / (sec2A – 1)½

(v) cot A

We know

cot A = cos A / sin A

cot A = (1/sec A) / ((sec2A – 1)1/2 / sec A)

cot A = 1 / (sec2A – 1)1/2

Question 3. Evaluate:  

(i) (sin2 63° + sin2 27°)/(cos2 17° + cos2 73°)

(ii) sin 25° cos 65° + cos 25° sin 65°

(i) ([sin(90-27)]2 + sin2 27) / ([cos(90-73)]2 + cos2 73)

We know that 

sin(90-x) = cos x
cos(90-x) = sin x

(cos2(27) + sin2 27) / (sin2(73) + cos2 73)

Using 

sin2A + cos2A = 1

1/1 = 1

(ii) [sin 25 * cos(90-25)] + [cos 25 * sin(90-25)]

Using

sin(90-x) = cos x
cos(90-x) = sin x

= [sin 25 * sin 25] + [cos 25 * cos 25]

= sin2 25 + cos2 25

Question 4. Choose the correct option. Justify your choice.  

Solution:

(i) 9 sec2 A – 9 tan2 A  

(A) 1 (B) 9 (C) 8 (D) 0 

Using sec2A – tan2A = 1 

9 (sec2A – tan2A ) = 9(1) 

Ans (B) 

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)

(A) 0 (B) 1 (C) 2 (D) –1 

Simplifying all ratios

= (1 + sinθ/cosθ + 1/cosθ) (1 + cosθ/sinθ – 1/sinθ)

= ((cosθ + sinθ + 1)/ cosθ) ((sinθ + cosθ – 1 )/sinθ)

= ((cosθ + sinθ)2 – 1) / (sinθ cosθ)

= (1 + 2*cosθ*sinθ – 1) / (sinθ cosθ)

Ans (C)

(iii) (sec A + tan A) * (1 – sin A) 

(A) sec A (B) sin A (C) cosec A (D) cos A 

Simplifying sec A and tan A

= (1/cos A + sin A/cos A)*(1 – sin A)

= ((1 + sin A)/cos A)*(1 – sin A)

= (1 – sin2A)/cos A

= cos2A / cos A

= cos A

Ans (D)

(iv) (1 + tan2A) / (1 + cot2A)

(A) sec2A (B) –1 (C) cot2A (D) tan2A

Simplifying tan A and cot A

= (1 + (sin2A / cos2A)) / (1 + (cos2A / sin2A))

= ((cos2A + sin2A) / cos2A) / ((cos2A + sin2A) / sin2A)

= sin2A / cos2A

= tan2A

Ans (D)

Question 5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Solution:

(i) (cosec θ – cot θ)2 = (1 – cosθ) / (1 + cosθ)

Solving LHS

Simplifying cosec θ and cot θ

= (1-cos θ)2 / sin2θ

= (1-cos θ)2 / (1-cos2θ)

Using a2 – b2 = (a+b)*(a-b)

= (1-cos θ)2 / [(1-cos θ)*(1+cos θ)]

= (1-cos θ) / (1+cos θ) = RHS

Hence Proved

(ii) (cos A / (1+sin A) + ((1+sin A) / cos A) = 2 sec A

Solving LHS

Taking LCM 

= (cos2A + (1+sin A)2) / ((1+sin A) cos A)

= (cos2A + 1 + sin2A + 2 sin A ) / ((1 + sin A)*cos A)

Using sin2A + cos2A = 1

= (2 + 2*sin A) / ((1+sin A)*cos A)

= (2*(1 + sin A)) / ((1 + sin A)*cos A)

= 2 / cos A

= 2 sec A = RHS

Hence Proved

(iii) (tan θ / (1 – cot θ)) + (cot θ / (1 – tan θ)) = 1 + sec θ*cosec θ

Solving LHS

Changing tan θ and cot θ in terms of sin θ and cos θ and simplifying

= ((sin2θ) / (cos θ *(sin θ-cos θ))) + ((cos2θ ) / (sin θ *(sin θ-cos θ)))

= (1 / (sin θ-cos θ)) * [(sin3θ – cos3θ) / (sin θ * cos θ)]

= (1 / (sin θ – cos θ)) * [ ((sin θ – cos θ) * ( sin2θ + cos2θ + sin θ * cos θ ))/(sin θ *cos θ)]

= (1+sin θ*cos θ) / (sin θ*cos θ)

= sec θ*cosec θ + 1 = RHS

Hence Proved

(iv) (1 + sec A) / sec A = sin2A / (1 – cos A)

Solving LHS

= cos A + 1

Solving RHS

= (1 – cos2A) / (1 – cos A)

= (1 – cos A) * (1 + cos A) / (1 – cos A)

= 1 + cos A = RHS

Hence Proved

(v) (cos A – sin A + 1) / (cos A + sin A – 1) = cosec A + cot A using the identity cosec2A = 1 + cot2A

Solving LHS

Multiplying numerator and denominator by (cot A – 1 + cosec A)

= (cot2A + 1 + cosec2A – 2*cot A – 2*cosec A + 2*cot A*cosec A) / (cot2A – (1 + cosec2A – 2*cosec A))

= (2*cosec2A – 2*cot A – 2*cosec A + 2*cot A*cosec A) / (cot2A – 1 – cosec2A + 2*cosec A) 

= (2* cosec A *(cosec A + cot A) – 2*(cosec A + cot A)) / (cot2A – 1 – cosec2A + 2*cosec A)

= ((cosec A + cot A) * (2*cosec A – 2 )) / (2*cosec A – 2) 

= cosec A + cot A = RHS

Hence Proved

(vi) [(1 + sin A) / (1 – sin A)]½ = sec A + tan A

Solving LHS

Multiplying numerator and denominator by (1+sinA)

= [((1 + sin A)*(1 + sin A)) / ((1 – sin A)*(1 + sin A))]½

= (1 + sin A) / (1 – sin2A)½

= (1 + sin A) / (cos2A)1/2

= (1 + sin A) / (cos A)

= sec A + tan A = RHS

Hence Proved

(vii) (sin θ – 2 sin3θ) / (2 cos3θ – cos θ) = tan θ

Solving LHS

= (sin θ * (1 – 2*sin2θ)) / (cos θ * (2*cos2θ – 1))

= (sin θ * (1 – 2*sin2θ )) / (cos θ * (2*(1 – sin2θ) – 1))

= (sin θ *(1 – 2*sin2θ)) / (cos θ * (1 – 2*sin2θ))

= tan θ = RHS

Hence Proved 

(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2A + cot2A

Solving LHS

= sin2A + cosec2A + 2*sin A *cosec A + cos2A + sec2A + 2*cos A *sec A

We know that cosec A = 1 / sin A

= 1 + 1 + cot2A + 1 + tan2A + 2 + 2

= 7 + tan2A + cot2A = RHS

Hence Proved

(ix) (cosec A – sin A)*(sec A – cos A) = 1 / (tan A + cot A)

Solving LHS

= ((1/sin A) – sin A) * ((1/cos A) – cos A)

= ((1 – sin2A) / sin A) * ((1 – cos2A) / cos A)

= (cos2A * sin2A) / (sin A * cos A)

= sin A * cos A

Solving RHS

Simplifying tan A and cot A

= (sin A * cos A) / ( sin2A + cos2A)

= sin A * cos A = RHS

Hence Proved

(x) (1 + tan2A) / (1 + cot2A ) = [(1 – tan A) / (1 – cot A)]2 = tan2A

Solving LHS

Changing cot A = 1 / tan A

= (tan2A * (1 + tan2A)) / (1 + tan2A) = tan2A = RHS

= [(1 – tan A) / (1 – cot A)]2 = (1 + tan2A – 2*tan A) / (1 + cot2A – 2*cot A)

= (sec2A – 2*tan A) / (cosec2A – 2*cot A)

Solving this we get 

= tan2A

Hence Proved

FAQs on NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Q1: Why is it important to learn Trigonometry?

Answer:

Trigonometry is used to set directions. It also tells you the direction to point the compass in order to travel straight forward. To locate a certain location, it is used in navigation. It is also employed to calculate the separation between a location in the water and the coast.

Q2: What topics are covered in NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry?

Answer:

NCERT Solutions for Class 10 Maths Chapter 8-Introduction to Trigonometry covers topics such as trigonometric ratios and their calculation with the help of Pythagoras theorem, calculation of some specific angles like 0 degrees, 30 degrees, 45 degrees, and 90 degrees and the use of the trigonometric table, complementary angle, and trigonometric identities. 

Q3: How can NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry help me?

Answer:

NCERT Solutions for Class 10 Maths Chapter 8-Introduction to Trigonometry can help you solve the NCERT exercise without any limitations. If you are stuck on a problem you can find its solution in these solutions and free yourself from the frustration of being stuck on some question.

Q4: How many exercises are there in Class 10 Maths Chapter 8 Introduction to Trigonometry?

Answer:

There are 4 exercises in the Class 10 Maths Chapter 8-Introduction to Trigonometry which covers all the important topics and sub-topics.

Q5: Where can I find NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry?

Answer:

You can find these NCERT Solutions in this article created by our team of experts at GeeksforGeeks.