A note on CF1809F (EDU145F) Traveling in Berland, O(n)!

Problem: Link

Submission: Link , 93ms!

Part1: Hint

By looking at the test cases, we find that answers for are the same.

Part2: The greedy strategy (for each index )

First, we define some macros for convenience:

The previous index of : #define pr(x) ((x) == 1 ? n : (x) - 1)

The next index of : #define ne(x) ((x) == n ? 1 : (x) + 1)

If , rt(x) denotes the place of the next in the loop: rt(x). For example, let be an -indexed array , then and . Note that could happen, for example, , then . rt could be pre-calculated using a stack.

get(i, j): The liters of gas we need to go from to , both inclusive and -indexed. might happen since our trip is a circle. For example, if , then and . The function could be pre-calculated using the prefix sum.

We need to maintain an array in the algorithm. denotes the minimum burbles we need to pay from the previous place where to . may be equal to . For example, if , then denotes the minimum burbles we need to pay from to , which is . denotes the minimum burbles we need to pay from to . Note that this is well-defined iff there's at least one such that . So we just need to output the case where all equal to .

//The Initialpoint
int i = initialpoint;
while(true){
    (1) If you are at the destination, which is the same as the initialpoint, goto finish.

    (2) When you stay at i where b[i]==2, just pay 2a[i] for a[i] liters that enables you to move from i to ne(i). let i = ne(i);

    (3) When you stay at i where b[i]==1, set initialized2 = true and curi = i, and do the following inner while loop. Also, we need to calculate the array c.
    while(initialized2 || curi != rt(i)){ 
        //rt(i): The next i in this trip with b[i]==1
        //Why do we need this initialized2? Because curi before the loop is i, which may be equal to rt(i) at the beginning, in this case we still need to go into this loop!
        if(curi == initialpoint) goto finish;
        initialized2 = false;
        if(get(i, curi) <= k) c[curi] = get(i, curi);
        else c[curi] = k + 2*(get(i, curi) - k); //Buy k liters at i using k burbles and the left get(i, curi) - k liters using 2*(get(i, curi) - k) burbles.
        curi = ne(curi);
    }
}
finish:

You may worry about the line if(get(i, curi) <= k) c[curi] = get(i, curi);. In this line, if get(i, curi) <= k, we just buy get(i, curi) instead of filling all liters into the tank. You may think it would be better if we grasp the chance (that we are at some good place that ) to make our tank full. But, our algorithm is correct. Whenever our algorithm is forced to buy one liter using two burbles, every other strategy needs to. If we have not met an such that in our trip, then we can only buy one liter using two burbles, no matter what our strategy is. Otherwise, if we are forced to buy one liter using two burbles at some place where , let be the last we meet (). According to our algorithm, , which means our algorithm already makes the tank full at place . Even if that, it still faces the lack of fuel issue at and has to pay for more expensive liter. For other strategies, the fuel amount is at most at place , so it must also face the lack of liter issue at , and has to pay for more expensive liter also!

When there is at least one in the array, it would be beneficial to decompose our trip into 1222222 blocks. There is at least one block. We would discover that when our trip starts at the leading 1 of the block, it always has liter! We can prove by induction that each block only buys the fuel it needs for this block. If there is a partial incomplete block before that leading 1, e.g., it starts at 2, goes like 22212222, and now we are at the fourth place 1. According to our algorithm, when it does not meet one 1, you only pay for the fuel that is sufficient for you to go to the next place. Therefore, you won't have any fuel left. Blocks are independent of each other, and if you start at , the answer would be the sum of these blocks, which is the same for each where .

Part3: The overall algorithm

First, we need to special judge the case where all . In this case, the answer for each is

We need this special judge, otherwise, the array in Part 2 would be ill-defined, and the blocks in the last paragraph of Part 2 would be ambiguous.

We denote the answer for each as answer1.

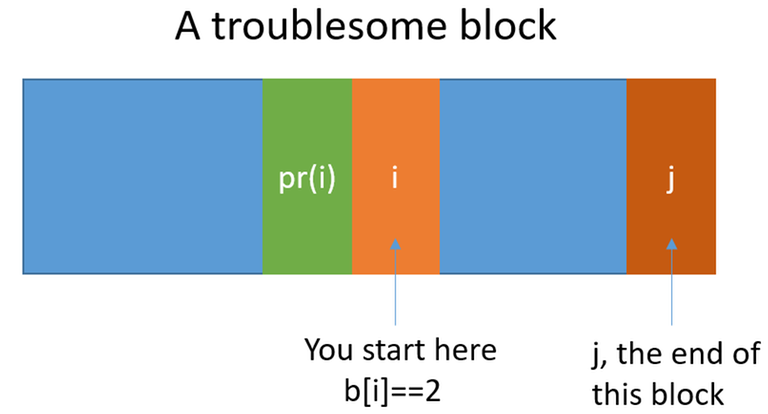
What is the answer when you start at (we call the block to which is affiliated the troublesome block)? It would be:

Since we don't go through the troublesome block, we need to discount the contribution of this block, which is from . To travel from to , we need burbles for liters of fuel. And is the burbles we need to pay from the start of this block (which we don't need to know) to , since we need to finish our trip at .