如何优化矩阵相乘

本文中所有的优化策略源自 How To Optimize Gemm，感谢 Prof. Robert van de Geijn 教授及其团队的付出！❤

我对原有的代码进行了一些改动，并放在了 junaire/HowToOptimizeGEMM 中。

矩阵相乘的定义

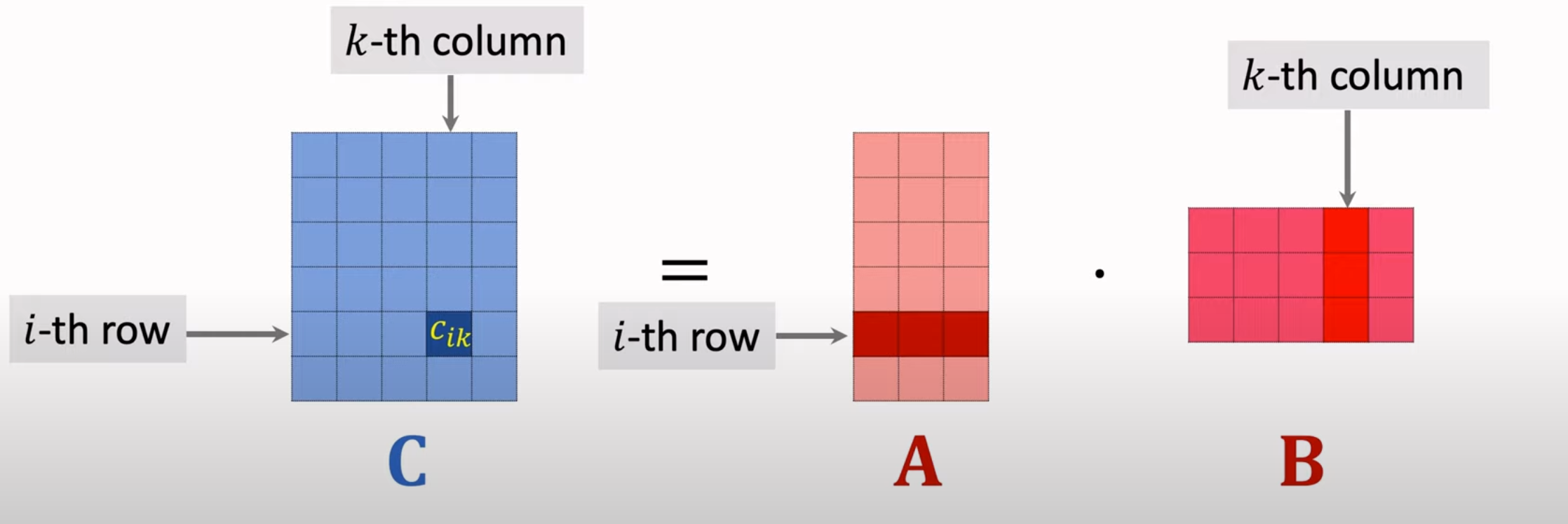
假设给定一个 m 行 p 列 的矩阵 A, 与一个 p 行 n 列的矩阵 B 相乘，结果可以得到一个 m 行 n 列的矩阵 C。C 中第 i 行，第 k 列的元素等于 A 中第 i 行的所有元素与 B 中第 k 列所有元素对应相乘的和。

朴素代码实现

根据定义我们可以得到一个最简单的 C 代码实现：

double A[m][k]; // m 行 k 列矩阵
double B[k][n]; // k 行 n 列矩阵
double C[m][n]; // m 行 n 列矩阵

for (int i = 0; i < m; ++i) {
    for (int j = 0; j < n; ++j) {
        for (int p = 0; p < k; ++p) {
            C[i][j] += A[i][p] * B[p][j];
        }
    }
}

在矩阵相乘中，我们用 FLOPS 来衡量算法的性能。FLOPS 指每秒浮点运算次数。也就是总的浮点数运算次数除以所花费的时间。

在矩阵相乘中，为了计算 C 中的一个元素，需要将 A 中第 i 行的 k 个元素与 B 中第 p 列的 k 个元素分别对应相乘得到 k 个结果并相加在一起。所以总共需要 2 * k 次浮点运算。矩阵 C 中总共有 m * n 个元素，所以总的浮点数运算次数，即 FLOPs 为 2 * m * n * k。

故矩阵相乘的 FLOPS 为 FLOPs / time_cost。

矩阵相乘的优化主要是访存优化。观察上面的朴素实现我们可以发现，对于矩阵 A，我们总是在做步长为1的访存，而对于矩阵 B，我们的每次元素访问跨度都是 n，即矩阵的宽度。这显然对缓存是不友好的，我们需要尽可能的减小访存步长，从而提高高速缓存命中率。

首先我们要做的是将行主序储存的矩阵转换为列主序储存。（或者说矩阵的转置）

定义下列宏：

#define A(i, j) a[(j)*lda + (i)]
#define B(i, j) b[(j)*ldb + (i)]
#define C(i, j) c[(j)*ldc + (i)]

其中 lda，ldb 与 ldc 分别代表的是矩阵 A，B 和 C 的高度。

我们用一个一维向量来储存整个矩阵，举个例子：

#include <stdio.h>
#include <stdlib.h>

#define A(i, j) a[(j)*lda + (i)]

int main() {
  int lda = 3;
  int k = 3;
  // lda 行，k 列的矩阵。
  double* a = malloc(sizeof(double) * (lda * k));
  A(0,0) = 1.00; A(0,1) = 2.00; A(0,2) = 3.00;
  A(1,0) = 4.00; A(1,1) = 5.00; A(1,2) = 6.00;
  A(2,0) = 7.00; A(2,1) = 8.00; A(2,2) = 9.00;

  for (double* p = a; p < a + (lda * k); ++p) {
    printf("%.2lf ", *p);
  }
  printf("\n");
}

输出结果为：

1.00 4.00 7.00 2.00 5.00 8.00 3.00 6.00 9.00

可以清楚地看到，矩阵 A 是一列一列在内存中储存的，即相邻列之间是连续的，这与传统上储存二维矩阵的形式刚好相反。

我们用一个简单的例子来说明具体的优化策略：

首先我们定义三个 4x4 的矩阵 A，B 和 C。C = A x B。有下述代码实现：

int m = 4;
int n = 4;
int k = 4;
int lda, ldb, ldc = 4;

// 一次计算一行的4个元素。由于列和行长度都是4，所以计算4次。
for (int j = 0; j < n; j += 4) {
    for (int i = 0; i < m; ++i) {
        // C(i, j) => 第 i 行，第 j 列元素。
        // A(i, 0) => 第 i 行，第 0 列元素。
        // B(0, j) => 第 0 行，第 j 列元素。
        AddDot1x4(k, &A(i, 0), lda, &B(0, j), &C(i, j), ldc);
    }
}

我们再以计算第0行4个元素，即第一次执行 AddDot1x4 为例，解释运算过程。

c00 = (a00 * b00) + (a01 * b10) + (a02 * b20) + (a03 * b30)
c01 = (a00 * b01) + (a01 * b11) + (a02 * b21) + (a03 * b31)
c02 = (a00 * b02) + (a01 * b12) + (a02 * b22) + (a03 * b32)
c03 = (a00 * b03) + (a01 * b13) + (a02 * b23) + (a03 * b33)

观察上述公式，我们可以发现每个元素的计算都分为4个部分，每个元素的第 i 个部分都访问了矩阵 A 中相同的元素，而一个元素4个部分对矩阵 B 的访问是内存连续的。所以我们可以改变循环方式，抛弃之前用一个循环计算 C 中一个元素的方法，即：

for (p = 0; p < k; p++) { C(0, 0) = C(0, 0) + A(0, p) * B(p, 0); }
for (p = 0; p < k; p++) { C(0, 1) = C(0, 1) + A(0, p) * B(p, 1); }
for (p = 0; p < k; p++) { C(0, 2) = C(0, 2) + A(0, p) * B(p, 2); }
for (p = 0; p < k; p++) { C(0, 3) = C(0, 3) + A(0, p) * B(p, 3); }

改成用一个大循环，每次计算这4个元素的一部分：

for (p = 0; p < k; p++) {
  // cij  =             a0p   *   bp0
  C(0, 0) = C(0, 0) + A(0, p) * B(p, 0);
  C(0, 1) = C(0, 1) + A(0, p) * B(p, 1);
  C(0, 2) = C(0, 2) + A(0, p) * B(p, 2);
  C(0, 3) = C(0, 3) + A(0, p) * B(p, 3);
}

在第一种循环方式内，A 的每次访问都是跨步为 lda，而 B 则是连续的。所以，总的需要跨步为 lda 的访存次数是 4 * k。而第二种方法由于复用了 A，所以跨步为 lda 的访存次数为 k。

减少访存次数

注意 A(0,p) 的含义实际为 a[p * lda]， 所以这实际上是一次很昂贵的访存操作。但是从上面的优化版循环我们可以看到，在一次循环里它是被共用的，而且是只读，所以我们可以一次循环只访存一次，将其存到一个局部变量中，指导编译器将其放入更高速的寄存器中。

再者就是对矩阵 C 的访问，由于我们相当于是在对其一个元素不断累加，所以我们根本不必每加一次就做一次访存，可以将临时结果暂存起来，循环退出后再做一次写入。

c_00 = 0.0;
c_01 = 0.0;
c_02 = 0.0;
c_03 = 0.0;

for (p=0; p < k; p++){
  a_0p = A( 0, p );

  c_00 += a_0p * B(p, 0);
  c_01 += a_0p * B(p, 1);
  c_02 += a_0p * B(p, 2);
  c_03 += a_0p * B(p, 3);
}

C(0, 0) += c_00;
C(0, 1) += c_01;
C(0, 2) += c_02;
C(0, 3) += c_03;

如此，我们便大大减少了不必要的昂贵访存操作，消除了一部分的访存延迟。

减少索引开销

在上面的代码片段中我们可以看到，B(p,0) 的变化过程为：

B(0,0) -> B(1,0) -> B(2,0) -> B(3,0)

也就是下一个要访问的元素为同行下一列的元素。由于矩阵在内存中是列主序储存的，所以也就是在访问下一个元素，步长为1。同理对 B(p,1)，B(p,2)，B(p,3) 都是成立的。

于是我们可以创建4个指针，分别指向第0行4列的四个元素，循环一次便递增一次指针，实现访问下一个元素。如图所示：

  bp0  bp1  bp2  bp3
   |    |    |    |
  \ /  \ /  \ /  \ /
+----+----+----+----+
|b00 |b01 |b02 |b03 |
+----+----+----+----+
|    |    |    |    |
+----+----+----+----+
|    |    |    |    |
+----+----+----+----+
|    |    |    |    |
+----+----+----+----+

代码示例如下：

bp0 = &B(0, 0);
bp1 = &B(0, 1);
bp2 = &B(0, 2);
bp3 = &B(0, 3);

c_00 = 0.0;
c_01 = 0.0;
c_02 = 0.0;
c_03 = 0.0;

for (p=0; p<k; p++){
  a_0p = A(0, p);

  c_00 += a_0p * *bp0++;
  c_01 += a_0p * *bp1++;
  c_02 += a_0p * *bp2++;
  c_03 += a_0p * *bp3++;
}

C(0, 0) += c_00;
C(0, 1) += c_01;
C(0, 2) += c_02;
C(0, 3) += c_03;

我们一次计算4行4列共16个元素，即：

// 一次计算4行共16个元素。由于我们的矩阵比较小，
// 列和行长度都是4，所以只计算1次。
for (int j = 0; j < n; j += 4) {
    for (int i = 0; i < m; i += 4) {
        // C(i, j) => 第 i 行，第 j 列元素。
        // A(i, 0) => 第 i 行，第 0 列元素。
        // B(0, j) => 第 0 行，第 j 列元素。
        AddDot4x4(k, &A(i, 0), lda, &B(0, j), &C(i, j), ldc);
    }
}

在使用之前所提到的技巧，可以得到：

b_p0 = &B(0, 0);
b_p1 = &B(0, 1);
b_p2 = &B(0, 2);
b_p3 = &B(0, 3);

for (p = 0; p < k; p++) {
  a_0p = A(0, p);
  a_1p = A(1, p);
  a_2p = A(2, p);
  a_3p = A(3, p);

  b_p0 = *b_p0++;
  b_p1 = *b_p1++;
  b_p2 = *b_p2++;
  b_p3 = *b_p3++;

  /* First row */
  c_00 += a_0p * b_p0;
  c_01 += a_0p * b_p1;
  c_02 += a_0p * b_p2;
  c_03 += a_0p * b_p3;

  /* Second row */
  c_10 += a_1p * b_p0;
  c_11 += a_1p * b_p1;
  c_12 += a_1p * b_p2;
  c_13 += a_1p * b_p3;

  /* Third row */
  c_20 += a_2p * b_p0;
  c_21 += a_2p * b_p1;
  c_22 += a_2p * b_p2;
  c_23 += a_2p * b_p3;

  /* Four row */
  c_30 += a_3p * b_p0;
  c_31 += a_3p * b_p1;
  c_32 += a_3p * b_p2;
  c_33 += a_3p * b_p3;
}
// 将 c_ij 赋值给 C(i, j)。

我们再计算下跨步为 lda 的访存次数。文章开头所提到的朴素实现中， A 的每次访问都是跨步为 lda，而 C 中一个元素需要访问 A 次数为 k，所以16个元素需要 16 * k 次访存跨步为 lda 的元素。而这里的优化版本一次循环需要访问 4 次，所以总的次数仅为 4 * k。

我们可以对上面的循环重新排列，指导编译器将序列化的循环转换为指令级的并行化计算。

/* First row and second rows */
// 可以看到 a_0p 与 a_1p 为同行相邻列的元素，内存中连续。
c_00 += a_0p * b_p0;
c_10 += a_1p * b_p0;

c_01 += a_0p * b_p1;
c_11 += a_1p * b_p1;

c_02 += a_0p * b_p2;
c_12 += a_1p * b_p2;

c_03 += a_0p * b_p3;
c_13 += a_1p * b_p3;

/* Third and fourth rows */
// 可以看到 a_2p 与 a_3p 为同行相邻列的元素，内存中连续。
c_20 += a_2p * b_p0;
c_30 += a_3p * b_p0;

c_21 += a_2p * b_p1;
c_31 += a_3p * b_p1;

c_22 += a_2p * b_p2;
c_32 += a_3p * b_p2;

c_23 += a_2p * b_p3;
c_33 += a_3p * b_p3;

由于 c00 与 c10 再内存中连续，a0p 与 a1p 再内存中连续，所以我们可以用一个向量寄存器来储存这两个元素，并通过向量指令同时计算他们的结果。

我们先定义一个 union：

typedef union {
  __m128d v; // 1个 double 有8字节，即64比特，所以可以存两个 double
  double d[2];
} v2df_t;

在计算时我们以 __m128d 的类型解释它，并在最后赋值后以两个 double 的形式解释它。

b_p0 = &B(0, 0); b_p1 = &B(0, 1); b_p2 = &B(0, 2); b_p3 = &B(0, 3);

c_00_c_10.v = _mm_setzero_pd();
c_01_c_11.v = _mm_setzero_pd();
c_02_c_12.v = _mm_setzero_pd();
c_03_c_13.v = _mm_setzero_pd();
c_20_c_30.v = _mm_setzero_pd();
c_21_c_31.v = _mm_setzero_pd();
c_22_c_32.v = _mm_setzero_pd();
c_23_c_33.v = _mm_setzero_pd();

for (p = 0; p < k; p++) {
  // 同时加载第 p 行两个元素到向量寄存器中。
  a_0p_a_1p.v = _mm_load_pd((double *)&A(0, p));
  a_2p_a_3p.v = _mm_load_pd((double *)&A(2, p));

  // 将 b_p0，即一个 double 分别加载到向量寄存器中两个元素中。
  b_p0.v = _mm_loaddup_pd((double *)b_p0++);
  b_p1.v = _mm_loaddup_pd((double *)b_p1++);
  b_p2.v = _mm_loaddup_pd((double *)b_p2++);
  b_p3.v = _mm_loaddup_pd((double *)b_p3++);

  /* First row and second rows */
  c_00_c_10.v += a_0p_a_1p.v * b_p0.v;
  // 上面运算相当于之前的：
  // c_00 += a_0p * b_p0;
  // c_10 += a_1p * b_p0;

  // 同理可看待下面的每个运算，由于一次计算两个元素，所以运算次数也从16次降为了8次。
  c_01_c_11.v += a_0p_a_1p.v * b_p1.v;
  c_02_c_12.v += a_0p_a_1p.v * b_p2.v;
  c_03_c_13.v += a_0p_a_1p.v * b_p3.v;

  /* Third and fourth rows */
  c_20_c_30.v += a_2p_a_3p.v * b_p0.v;
  c_21_c_31.v += a_2p_a_3p.v * b_p1.v;
  c_22_c_32.v += a_2p_a_3p.v * b_p2.v;
  c_23_c_33.v += a_2p_a_3p.v * b_p3.v;
}

C(0, 0) += c_00_c_10.d[0];
C(1, 0) += c_00_c_10.d[1];
// 省略赋值操作。