理解树状数组这一篇文章就够啦 - Cattle_Horse - JOYK Joy of Geek, Geek News, Link all geek

理解树状数组这一篇文章就够啦 - Cattle_Horse - 博客园

TODO：

二维树状数组
维护不可差分信息
补充题目

在阅读本文之前，您可能需要先了解位运算、二叉树以及前缀和与差分等相关知识

本文中，若无特殊说明，数列下标均从 1 开始

什么是树状数组

树状数组是一种通过数组来模拟"树形"结构，支持单点修改和区间查询的数据结构

因为它是通过二进制的性质构成的，所以它又被叫做 二进制索引树（BinaryIndexedTree），也被称作 FenWickTree

用于解决什么问题

树状数组常用于动态维护区间信息

P3374 【模板】树状数组 1 - 洛谷

题目简述：对数列进行单点修改以及区间求和

单点修改的时间复杂度为 O(1)

区间求和的时间复杂度为 O(n)

共 m 次操作，则总时间复杂度为 O(n×m)

java

import java.io.*;

public class Main {
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        int n = get(), m = get();
        int[] a = new int[n];
        for (int i = 0; i < n; ++i) a[i] = get();
        while (m-- != 0) {
            int command = get(), x = get(), y = get();
            if (command == 1) {
                a[x - 1] += y;
            } else {
                int sum = 0;
                for (int i = x - 1; i < y; i++) sum += a[i];
                out.println(sum);
            }
        }
        out.close();
    }
}

前缀和解法

区间求和通过前缀和优化，但单点修改的时候需要修改前缀和数组

单点修改的时间复杂度为 O(n)

区间求和的时间复杂度为 O(1)

共 m 次操作，则总时间复杂度为 O(n×m)

java

import java.io.*;

public class Main {
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        int n = get(), m = get();
        int[] sum = new int[n + 1];
        for (int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + get();
        while (m-- != 0) {
            int command = get(), x = get(), y = get();
            if (command == 1) {
                for (int i = x; i <= n; ++i) sum[i] += y;
            } else {
                System.out.println(sum[y] - sum[x - 1]);
            }
        }
        out.close();
    }
}

树状数组解法

可以发现上述两种方法，不是单点修改的时间复杂度过高，就是区间求和的时间复杂度过高，导致最坏时间复杂度很高。

于是，树状数组出现了，它用来平衡这两种操作的时间复杂度。

树状数组的思想

每个正整数都可以表示为若干个 2 的幂次之和（二进制基本原理）

类似的，每次求前缀和，我们也希望将区间 [1,i] 分解成 log2⁡i 个子集的和

也就是如果 i 的二进制表示中如果有 k 个 1，我们就希望将其分解为 k 个子集之和

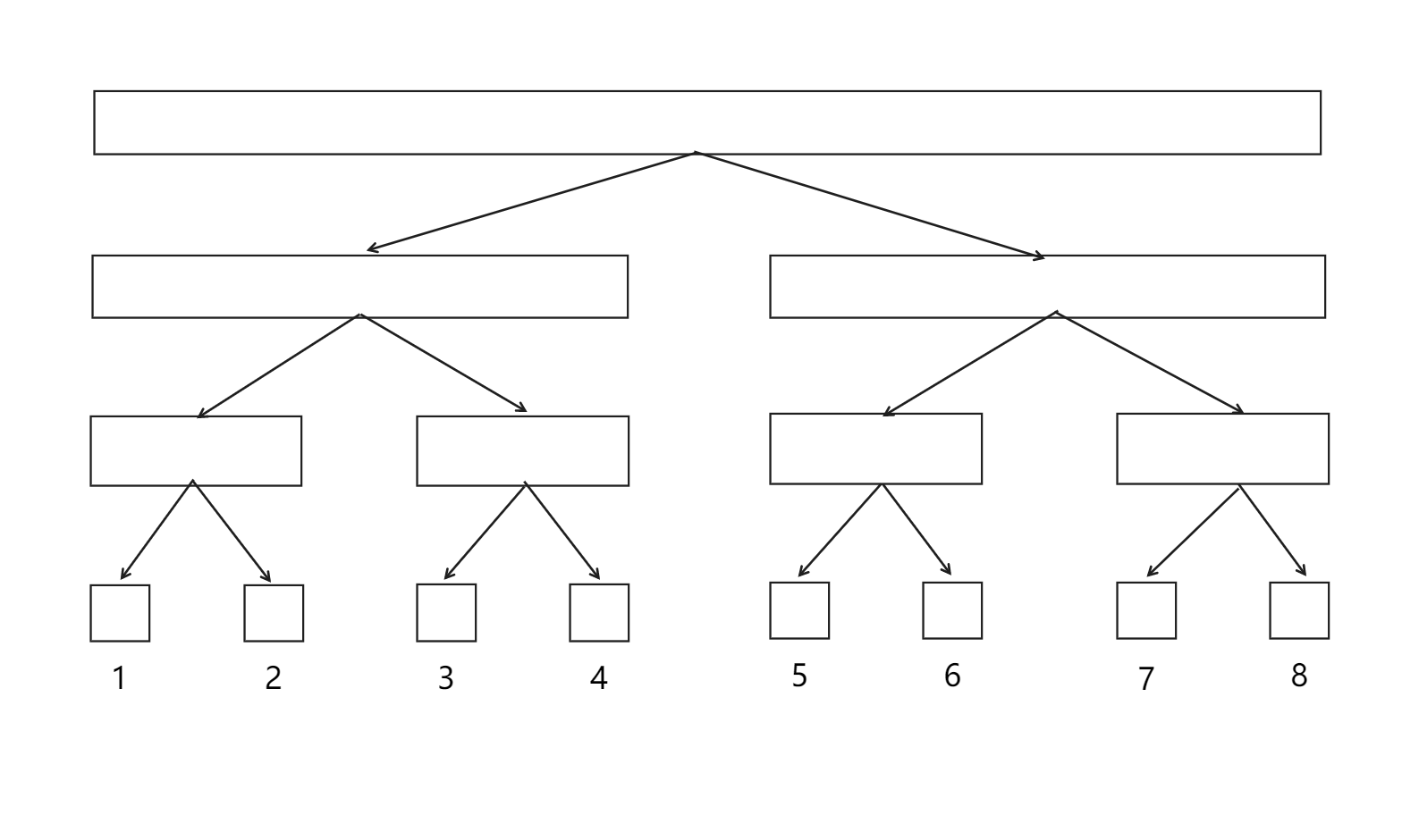
树状数组的树形态与二叉树

每一个矩形代表树的一个节点，矩形大小表示所管辖的数列区间范围

一颗二叉树的形态如下图所示

我们发现，对于具有逆运算的运算，如求和运算，有如下式子

sum(l,r)=sum(l,k)+sum(k+1,r)sum(k+1,r)=sum(l,r)−sum(l,k)

实际上，许多数据可以通过一些节点的差集获得

因此，上述二叉树的一些节点可以进行删除

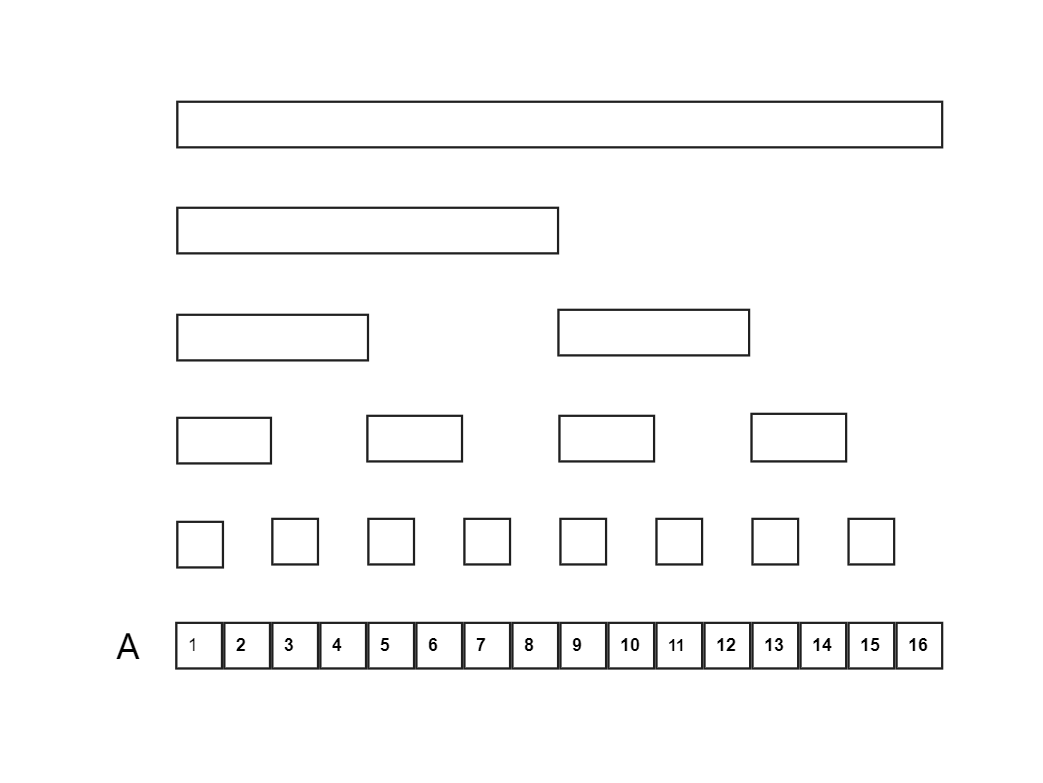
树状数组的形态如下图所示

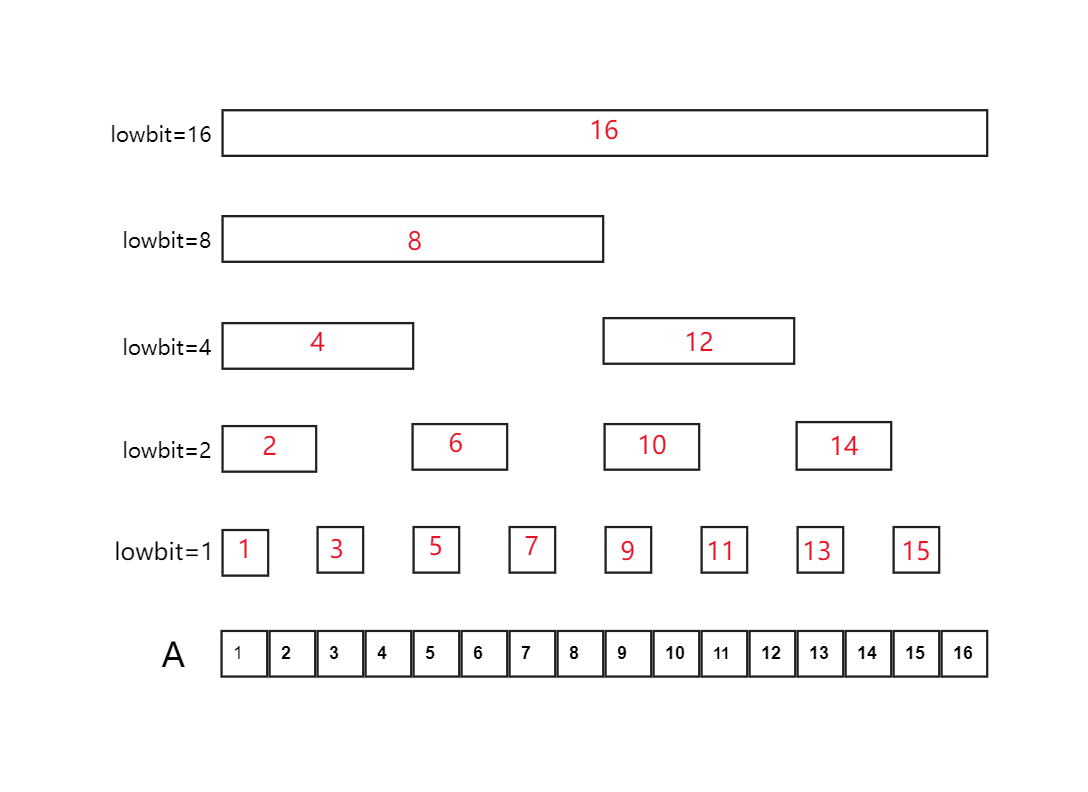
对于下图中的树状数组（黑色数字代表原始数组 Ai 红色数字代表树状数组中的每个节点数据 Ci）

从图中可以看出：

树状数组	管辖区间
C1	A[1…1]
C2	A[1…2]
C3	A[3…3]
C4	A[1…4]
C5	A[5…5]
C6	A[5…6]
C7	A[7…7]
C8	A[1…8]

那么如何通过计算机确定 Cx 的管辖区间呢？

前面提到过树状数组的思想是基于二进制的

树状数组中，规定 Cx 所管辖的区间长度为 2k，其中：

设二进制最低位为第 0 位，则 k 恰好为 x 的二进制表示中，最低位的 1 所在的二进制位数；
2k（Cx 的管辖区间长度）恰好为 x 二进制表示中，最低位的 1 以及后面所有 0 组成的数。

以 C88 所管辖的区间为例

因为 (88)10=(1011000)2，其二进制最低位的 1 及后面的 0 组成的二进制是 (1000)2=(8)10，所以，C88 管理 8 个 A 数组中的元素。

因此，C88 代表 A[81…88] 的区间信息。

我们记 x 二进制最低位 1 以及后面的 0组成的数为 lowbit(x)，则 Cx 管辖的区间就是 A[x−lowbit(x)+1,x]

其中 lowbit(x) = x & (~x + 1) = x & -x

树状数组树的性质

性质比较多，下面列出重要的几个性质，更多性质请参见OI Wiki，下面表述忽略二进制前导零

节点 u 的父节点为 u+lowbit(u)
设节点 u=s×2k+1+2k，则其儿子数量为 k=log2lowbit(u)（即 u 的二进制表示中尾随 0 的个数），这 k 个儿子的编号分别为 u−2t(0≤t<k)

如 k=3，u 的二进制表示为 1000，则 u 有三个儿子，这三个儿子的二进制编号分别为 111、110、100
节点 u 的所有儿子对应 Cu 的管辖区间恰好拼接成 [lowbit(u),u−1]
- 如 k=3，u 的二进制表示为 1000，u 的三个儿子的二进制编号分别为 111、110、100
  
  C[100]表示A[001~100]，C[110]表示A[101~110]，C[111]表示A[111~111]
  
  上述三个儿子管辖区间的并集恰好是 A[001~111]，即 [lowbit(u),u−1]

根据管辖区间，逐层维护管辖区间包含这个节点的父节点（节点 u 的父节点为 u+lowbit(u)）

java

void add(int x, int val) { // A[x] 加上 val
    for (; x <= n; x += x & -x) {
        C[x] += val;
    }
}

区间查询问题可以转化为前缀查询问题（前缀和思想），也就是查询区间 [l,r] 的和，可以转化为 A[1…r]与A[1…l−1]的差集

如计算 A[4…7] 的值，可以转化为求 A[1…7] 和 A[1…3] 再相减

前缀查询的过程是：根据管辖区间，不断拆分区间，查找上一个前缀区间

对于 A[1…x] 的前缀查询过程如下：

从 x 开始向前拆分，有 Cx 管辖 A[x−lowbit(x)+1…x]
令 x←x−lowbit(x)
重复上述过程，直至 x=0

由于 x−lowbit(x) 的算术意义是去除二进制最后一个 1，因此也可以写为 x&(x−1)

java

// 查询前缀 A[1...x] 的和
int getSum(int x) {
    int ans = 0;
    for (; x != 0; x &= x - 1) ans += C[x];
    //for (; x != 0; x -= x & -x) ans += C[x];
    return ans;
}
// 查询区间 A[l...r] 的和
int queryRange(int l, int r) {
    return getSum(r) - getSum(l - 1);
}

上述过程进行了两次前缀查询，实际上，对于 l−1 和 r 的前缀区间是相同的，我们不需要计算

java

// 查询区间 A[l...r] 的和
int queryRange(int l, int r) {
    // return getSum(r) - getSum(l - 1);
    int ans = 0;
    --l;
    while (l < r) {
        // 左边层数低，左边向前跳
        int lowbitl = l & -l, lowbitr = r & -r;
        if (l != 0 && lowbitl < lowbitr) {
            ans -= C[l];
            l -= lowbitl;
        } else {
            ans += C[r];
            r -= lowbitr;
        }
    }
    return ans;
}

单点查询可以转化为区间查询，需要两次前缀查询，但有更好的方法

x 所管辖的区间为 Cx=A[x−lowbit(x)+1…x]，而节点 x 的所有子节点的并集恰好为 A[x−lowbit(x)+1…x−1]

则 A[x]=Cx−A[x−lowbit(x)+1…x−1]

对于 A[x] 的更好的查询过程如下：

查询 x 所管辖的区间 Cx
减去 x 的所有子节点的数据

java

//int queryOne(int x) {
//    return queryRange(x, x);
//}
int queryOne(int x) {
    int ans = c[x];
    int lca = x & x - 1; // x - lowbit(x)
    for (int i = x - 1; i > lca; i &= i - 1) {
        ans -= C[i];
    }
    return ans;
}

可以通过调用单调修改方法进行建树，时间复杂度 O(nlog⁡n)

时间复杂度为 O(n) 的建树方法有如下两种：

每一个节点的值是由所有与自己直接相连的儿子的值求和得到的。因此可以倒着考虑贡献，即每次确定完儿子的值后，用自己的值更新自己的直接父亲。

java

void init() {
    for (int i = 1; i <= n; ++i) {
        C[i] += A[i];
        // 找 i 的父节点
        int father = i + (i & -i);
        if (father <= n) C[father] += C[i];
    }
}

由于 Cx 所管辖的区间是 [x−lowbit(x)+1,x]，则可以预处理 sum 前缀和数组，再通过 sum[x]−sum[x−lowbit(x)] 计算 Cx

我们也可以先用 C 数组计算前缀和，再倒着计算 Cx（因为正着计算会导致前面的值被修改，与 01 背包优化相同）

同样的 x−lowbit(x) 可以写为 x&(x−1)

java

void init() {
    for (int i = 1; i <= n; ++i) {
        C[i] = C[i - 1] + A[i];
    }
    for (int i = n; i > 0; --i) {
        C[i] -= C[i & i - 1];
    }
}

复杂度分析

空间复杂度为 O(n)

单点修改、单点查询、区间查询操作的时间复杂度均为 O(log⁡n)

建树的时间复杂度为 O(nlog⁡n) 或 O(n)

java

import java.io.*;

public class Main {
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    static int n;
    static int[] c, a;

    static void add(int x, int val) {
        for (; x <= n; x += x & -x) {
            c[x] += val;
        }
    }

    static int getSum(int x) {
        int ans = 0;
        for (; x != 0; x &= x - 1) ans += c[x];
        return ans;
    }

    static int queryOne(int x) {
        int ans = c[x];
        int lca = x & x - 1;
        for (int i = x - 1; i > lca; i &= i - 1) {
            ans -= c[i];
        }
        return ans;
    }

    static int queryRange(int l, int r) {
        int ans = 0;
        --l;
        while (l < r) {
            // 左边层数低，左边向前跳
            int lowbitl = l & -l, lowbitr = r & -r;
            if (l != 0 && lowbitl < lowbitr) {
                ans -= c[l];
                l -= lowbitl;
            } else {
                ans += c[r];
                r -= lowbitr;
            }
        }
        return ans;
    }

    static void init() {
        for (int i = 1; i <= n; ++i) {
            c[i] += a[i];
            int father = i + (i & -i);
            if (father <= n) c[father] += c[i];
        }
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        n = get();
        int m = get();
        a = new int[n + 1];
        c = new int[n + 1];
        for (int i = 1; i <= n; ++i) a[i] = get();
        init();
        while (m-- != 0) {
            int command = get(), x = get(), y = get();
            if (command == 1) {
                add(x, y);
            } else {
                out.println(queryRange(x, y));
            }
        }
        out.close();
    }
}

注意树状数组的树型特征
x 的管辖元素个数为lowbit(x)，管辖区间为 [x−lowbit(x)+1,x]
树状数组中，x 的父节点编号为 x+lowbit(x)
树状数组的二叉查找树中，x 的父节点（也即前缀区间）编号为 x−lowbit(x)
树状数组是一个维护前缀信息的树型数据结构
树状数组维护的信息需要满足结合律以及可差分（因为一些数据需要通过其他数据的差集获得）两个性质，如加法，乘法，异或等

结合律：(x∘y)∘z=x∘(y∘z)，其中 ∘ 是一个二元运算符。

可差分：具有逆运算的运算，即已知 x∘y 和 x 可以求出 y
有时树状数组在其他辅助数组（如差分数组）的帮助下，可以解决更多的问题
由于树状数组需要逆运算抵消掉原运算（如加和减），而线段树只需要逐层拆分区间，在合并区间信息，并不需要抵消部分数值，所以说树状数组能解决的问题是线段树能解决的问题的子集
树状数组下标也可以从 0 开始，此时 x 的父节点编号为 x|(x+1)，x 的管辖元素个数为 x−(x&(x+1))+1，管辖区间为 [x&(x+1),x]

树状数组封装类

一个 Java 的树状数组封装类

java

class BIT {
    int n;
    int[] c;

    // 请保证 a 的数据从下标 1 开始
    public void init(int[] a) {
        // assert(a.length > n);
        for (int i = 1; i <= n; ++i) {
            c[i] += a[i];
            int father = i + (i & -i);
            if (father <= n) c[father] += c[i];
        }
    }

    public BIT(int _n) {
        n = _n;
        c = new int[n + 1];
    }

    // 请保证 a 的数据从下标 1 开始
    public BIT(int[] a, int _n) {
        n = _n;
        c = new int[n + 1];
        init(a);
    }

    public void add(int i, int val) {
        if (i > n) return;
        for (; i <= n; i += i & -i) {
            c[i] += val;
        }
    }

    public int preSum(int i) {
        int ans = 0;
        for (; i != 0; i &= i - 1) ans += c[i];
        return ans;
    }

    public int single(int i) {
        int ans = c[i];
        int lca = i & i - 1;
        for (int j = i - 1; j > lca; j &= j - 1) {
            ans -= c[j];
        }
        return ans;
    }

    public int range(int l, int r) {
        int ans = 0;
        --l;
        while (l < r) {
            // 左边层数低，左边向前跳
            int lowbitl = l & -l, lowbitr = r & -r;
            if (l != 0 && lowbitl < lowbitr) {
                ans -= c[l];
                l -= lowbitl;
            } else {
                ans += c[r];
                r -= lowbitr;
            }
        }
        return ans;
    }
}

区间修改+单点查询

P3368 【模板】树状数组 2 - 洛谷

一些操作映射到前缀数组或者差分数组上可能会变得很简单

考虑序列 a 的差分数组 d，其中 di=ai−ai−1。

则对于序列 a 的区间 [l,r] 加 value 可以转化为 dl+value 和 dr+1−value，也就是差分数组上的两次单点操作。

因此 ax=∑i=1xdi 选择通过树状数组维护差分数组

java

import java.io.*;

public class Main {
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    static int n;
    static int[] d, a;

    static void add(int x, int val) {
        for (; x <= n; x += x & -x) {
            d[x] += val;
        }
    }

    static int getSum(int x) {
        int ans = 0;
        for (; x != 0; x &= x - 1) ans += d[x];
        return ans;
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        n = get();
        int m = get();
        a = new int[n + 1];
        d = new int[n + 1];
        for (int i = 1; i <= n; ++i) a[i] = get();
        // 初始化 c[i] 为 0，仅在 c 上差分，可以不用对 a 进行差分
        while (m-- != 0) {
            int command = get();
            if (command == 1) {
                int x = get(), y = get(), k = get();
                if (k == 0) continue;
                add(x, k);
                if (y + 1 <= n) add(y + 1, -k);
            } else {
                int x = get();
                out.println(getSum(x) + a[x]);
            }
        }
        out.close();
    }
}

区间修改+区间查询

P3372 【模板】线段树 1 - 洛谷

对于区间查询 a[l…r]，同样选择转化为前缀查询 a[1…r] 及 a[1…l−1] 的差集

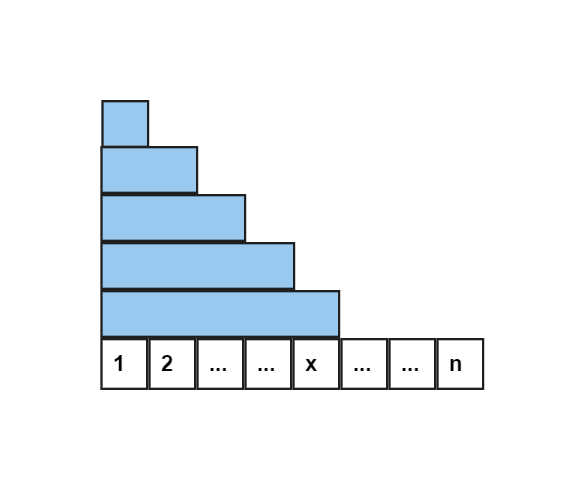
考虑序列 a 的差分数组 d，其中 di=ai−ai−1。由于差分数组的前缀和就是原数组，则 ai=∑j=1idj

所以，前缀查询变为 ∑i=1xai=∑i=1x∑j=1idj

上式可表述为下图蓝色部分面积

横着看看不出什么，但竖着看会发现每个数据加的个数与 x 有关

dx 会加 1 次，dx−1 会加 2 次，… ，d2 会加 x−1 次，d1 会加 x 次

也就是 di 会加 x−i+1，加法转化为乘法可得

∑i=1xai=∑i=1x∑j=1idj=∑i=1xdi×(x−i+1)=∑i=1xdi×(x+1)−∑i=1xdi×i=(x+1)×∑i=1xdi−∑i=1xdi×i

又因为 ∑i=1xdi 与 ∑i=1xdi×i 不能推导推导出另一个

因此需要用两个树状数组分别维护 di 与 di×i

用于维护 di 的树状数组，对于每次对 [l,r] 加 k 转化为 d[l]+k 与 d[r+1]−k
用于维护 di×i 的树状数组，对于每次对 [l,r] 加 k 转化为

(d[l]+k)×l=d[l]×l+l×k 与

(d[r+1]−k)×(r+1)=d[r+1]×(r+1)−(r+1)×k

即在原来的基础上加上 l×k 与减去 (r+1)×k

java

import java.io.*;

public class Main {

    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        int n = get(), m = get();
        int[] a = new int[n + 1];
        for (int i = 1; i <= n; ++i) {
            a[i] = get();
        }
        // 求前缀和
        for (int i = 1; i <= n; ++i) {
            a[i] += a[i - 1];
        }
        // 同样的，初始化为 0，仅在空数组上差分
        BIT tree1 = new BIT(n), tree2 = new BIT(n);
        while (m-- != 0) {
            int command = get(), x = get(), y = get();
            if (command == 1) {
                long k = get();
                tree1.add(x, k);
                tree1.add(y + 1, -k);
                tree2.add(x, x * k);
                tree2.add(y + 1, -(y + 1) * k);
            } else {
                // A[1...y] 的和
                long preY = a[y] + (y + 1) * tree1.preSum(y) - tree2.preSum(y);
                // A[1...x-1] 的和
                --x;
                long preX = a[x] + (x + 1) * tree1.preSum(x) - tree2.preSum(x);
                out.println(preY - preX);
            }
        }
        out.close();
    }
}

class BIT {
    int n;
    long[] c;

    // 请保证 a 的数据从下标 1 开始
    public void init(int[] a) {
        // assert(a.length > n);
        for (int i = 1; i <= n; ++i) {
            c[i] += a[i];
            int father = i + (i & -i);
            if (father <= n) c[father] += c[i];
        }
    }

    public BIT(int _n) {
        n = _n;
        c = new long[n + 1];
    }

    // 请保证 a 的数据从下标 1 开始
    public BIT(int[] a, int _n) {
        n = _n;
        c = new long[n + 1];
        init(a);
    }

    public void add(int i, long val) {
        if (i > n) return;
        for (; i <= n; i += i & -i) {
            c[i] += val;
        }
    }

    public long preSum(int i) {
        long ans = 0;
        for (; i != 0; i &= i - 1) ans += c[i];
        return ans;
    }

    public long single(int i) {
        long ans = c[i];
        int lca = i & i - 1;
        for (int j = i - 1; j > lca; j &= j - 1) {
            ans -= c[j];
        }
        return ans;
    }

    public long range(int l, int r) {
        long ans = 0;
        --l;
        while (l < r) {
            // 左边层数低，左边向前跳
            int lowbitl = l & -l, lowbitr = r & -r;
            if (l != 0 && lowbitl < lowbitr) {
                ans -= c[l];
                l -= lowbitl;
            } else {
                ans += c[r];
                r -= lowbitr;
            }
        }
        return ans;
    }
}

也可以写成封装类的形式

java

import java.io.*;

public class Main {

    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        int n = get(), m = get();
        int[] a = new int[n + 1];
        for (int i = 1; i <= n; ++i) {
            a[i] = get();
        }
        // 求前缀和
        for (int i = 1; i <= n; ++i) {
            a[i] += a[i - 1];
        }
        ExBIT tree = new ExBIT(n);
        while (m-- != 0) {
            int command = get(), x = get(), y = get();
            if (command == 1) {
                tree.add(x, y, get());
            } else {
                out.println(a[y] - a[x - 1] + tree.range(x, y));
            }
        }
        out.close();
    }
}

class BIT {
    int n;
    long[] c;

    // 请保证 a 的数据从下标 1 开始
    public void init(int[] a) {
        // assert(a.length > n);
        for (int i = 1; i <= n; ++i) {
            c[i] += a[i];
            int father = i + (i & -i);
            if (father <= n) c[father] += c[i];
        }
    }

    public BIT(int _n) {
        n = _n;
        c = new long[n + 1];
    }

    // 请保证 a 的数据从下标 1 开始
    public BIT(int[] a, int _n) {
        n = _n;
        c = new long[n + 1];
        init(a);
    }

    public void add(int i, long val) {
        if (i > n) return;
        for (; i <= n; i += i & -i) {
            c[i] += val;
        }
    }

    public long preSum(int i) {
        long ans = 0;
        for (; i != 0; i &= i - 1) ans += c[i];
        return ans;
    }

    public long single(int i) {
        long ans = c[i];
        int lca = i & i - 1;
        for (int j = i - 1; j > lca; j &= j - 1) {
            ans -= c[j];
        }
        return ans;
    }

    public long range(int l, int r) {
        long ans = 0;
        --l;
        while (l < r) {
            // 左边层数低，左边向前跳
            int lowbitl = l & -l, lowbitr = r & -r;
            if (l != 0 && lowbitl < lowbitr) {
                ans -= c[l];
                l -= lowbitl;
            } else {
                ans += c[r];
                r -= lowbitr;
            }
        }
        return ans;
    }
}

// 差分增量
class ExBIT {
    int n;
    BIT tree1, tree2;

    public ExBIT(int _n) {
        n = _n;
        tree1 = new BIT(_n);
        tree2 = new BIT(_n);
    }

    // 区间加对应差分数组的 两个端点操作
    public void add(int l, int r, long k) {
        tree1.add(l, k);
        tree1.add(r + 1, -k);
        tree2.add(l, l * k);
        tree2.add(r + 1, -(r + 1) * k);
    }

    // 差分增量的前缀和
    public long preSum(int i) {
        return (i + 1) * tree1.preSum(i) - tree2.preSum(i);
    }

    // 差分增量的区间和
    public long range(int l, int r) {
        return preSum(r) - preSum(l - 1);
    }
}

P4939 Agent2 - 洛谷

题目链接

题意简述：有两个操作

对区间 [l,r] 的数均加 1
查询第 x 个数的值

进阶中的区间修改+单点查询

java

import java.io.*;

public class Main {
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    static int n;
    static int[] d;

    static void add(int x, int val) {
        for (; x <= n; x += x & -x) {
            d[x] += val;
        }
    }

    static int getSum(int x) {
        int ans = 0;
        for (; x != 0; x &= x - 1) ans += d[x];
        return ans;
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        n = get();
        int m = get();
        d = new int[n + 1];
        while (m-- != 0) {
            int command = get();
            if (command == 0) {
                int x = get(), y = get();
                add(x, 1);
                if (y + 1 <= n) add(y + 1, -1);
            } else {
                int x = get();
                out.println(getSum(x));
            }
        }
        out.close();
    }
}

P5057 简单题 - 洛谷

题目链接

题目简述：有两个操作

对区间 [l,r] 的数进行反转（1变0，0变1）

反转等同于与 1 异或，于是题目变成了维护区间异或和单点查询，同样选择差分序列，只不过是异或的差分。

而异或也满足树状数组的两个要求，因此使用树状数组解决该题

java

import java.io.*;

public class Main {

    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    static int n, m;
    static int[] c;

    static void change(int x) {
        for (; x <= n; x += x & -x) c[x] ^= 1;
    }

    static int askPre(int x) {
        int ans = 0;
        for (; x != 0; x &= x - 1) ans ^= c[x];
        return ans;
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        n = get();
        m = get();
        c = new int[n + 1];
        while (m-- != 0) {
            int command = get();
            if (command == 1) {
                int l = get(), r = get();
                change(l);
                if (r < n) change(r + 1);
            } else {
                out.println(askPre(get()));
            }
        }
        out.close();
    }
}

P1908 逆序对 - 洛谷

题目链接

题意简述：求数组中的逆序对

求解逆序对可以用归并排序求解，此处不做讨论

从前向后遍历数组，同时将其加入到桶中，记录每个数出现的个数，并加上该位置之前且比当前数大的数的个数（有点绕，看例子可能会清晰点）

桶：用 cnt[i] 表示目前 i 出现的个数，初始化均为 0

ans：表示目前逆序对的个数，初始化为 0

txt

数组: 1 3 5 4 2 1                            桶的下标: 0 1 2 3 4 5 6
一: 加入 1 到桶中 ans+=cnt[2...max]     ans=0      桶: 0 1 0 0 0 0 0
二: 加入 3 到桶中 ans+=cnt[4...max]     ans=0      桶: 0 1 0 1 0 0 0
三: 加入 5 到桶中 ans+=cnt[6...max]     ans=0      桶: 0 1 0 1 0 1 0
四: 加入 4 到桶中 ans+=cnt[5...max]     ans=1      桶: 0 1 0 1 1 1 0
五: 加入 2 到桶中 ans+=cnt[3...max]     ans=4      桶: 0 1 1 1 1 1 0
六: 加入 1 到桶中 ans+=cnt[2...max]     ans=8      桶: 0 2 1 1 1 1 0

也就是需要求 i 时刻，桶中 [ai+1,max] 的和，其中 max 为所有数据中的最大值

也即实现单点加与区间查询，使用树状数组求解

但是题目中 max≤109，树状数组的长度开不了那么大

可以发现，该题中我们只关心数据间的相对大小关系，而不关心数据本身大小，采用离散化的方式，将数据缩小（一种映射关系）

举个例子：

txt

原数据: 1 100 200 500 50
新数据: 1 3 4 5 2
这样最大的数据就缩小到了 5

代码如下：

java

import java.io.*;
import java.util.Arrays;

public class Main {
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    static int get() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    static int n;
    static int[] d;

    static void add(int x, int val) {
        for (; x <= n; x += x & -x) {
            d[x] += val;
        }
    }

    static int getSum(int x) {
        int ans = 0;
        for (; x != 0; x &= x - 1) ans += d[x];
        return ans;
    }

    // 离散化
    static void lis(int[] a, int n) {
        int[] temp = new int[n];
        System.arraycopy(a, 0, temp, 0, n);
        Arrays.sort(temp);
        for (int i = 0; i < n; ++i) {
            a[i] = Arrays.binarySearch(temp, a[i]) + 1;
        }
    }

    public static void main(String[] args) throws IOException {
        PrintWriter out = new PrintWriter(System.out);
        n = get();
        int[] num = new int[n];
        for (int i = 0; i < n; ++i) num[i] = get();
        lis(num, n);
        d = new int[n + 1];
        long ans = 0;
        for (int i = 0; i < n; ++i) {
            add(num[i], 1);
            ans += i - getSum(num[i]) + 1;
        }
        out.println(ans);
        out.close();
    }
}

树状数组 - OI Wiki

__EOF__

理解树状数组这一篇文章就够啦 - Cattle_Horse

什么是树状数组

用于解决什么问题

前缀和解法

树状数组解法

树状数组的思想

树状数组的树形态与二叉树

树状数组树的性质

复杂度分析

树状数组封装类

区间修改+单点查询

区间修改+区间查询

P4939 Agent2 - 洛谷

P5057 简单题 - 洛谷

P1908 逆序对 - 洛谷

Recommend

Fortem bags $17.8M funding to meet counter-drone demand

Keychron Q12客制化机械键盘开售：数字小键盘居左，起售价928元

Mybatis Plus 框架项目落地实践总结 - CoderV的进阶笔记

Motorola Edge 40 Pro appears on Google Play Console with SD 8 Gen 2

索尼发布《生化危机8：村庄》VR 模式新预告

Minisforum举办2023年春季新品发布会：发布AMD平台新品，涵盖三个系列共五款

What makes a successful candidate for a top Chinese University?

Annual Planning in Uncertain Times: 6 Tactics for Rethinking Your Company’s End-...

【Oculus Interaction SDK】（十二）Meta Quest 如何开启透视（Passthrough） - 千叶C...

Airforms - Got a database, easily build data entry forms | Product Hunt

About Joyk