[Tutorial] On Range LIS Queries, Part 1

[Tutorial] On Range LIS Queries, Part 1

Hello, Codeforces!

At some point of life you want to make a new data structure problem with short statement and genius solution. LIS (Longest Increasing Subsequence) is a classic problem with beautiful solution, so you come up with the following problem:

• Given a sequence of length and queries , compute the length of Longest Increasing Subsequence of .

But on the other hand this looks impossible to solve, and you just give up the idea.

I always thought that the above problem is unsolved (and might be impossible), but very recently I learned that such queries are solvable in only time, not involving any sqrts! The original paper describes this technique as semi-local string comparison. The paper is incredibly long and uses tons of scary math terminology, but I think I found a relatively easier way to describe this technique, which I will show in this article.

Thanks to qwerasdfzxcl for helpful discussions, peltorator for giving me the motivation, and yosupo and noshi91 for preparing this problem.

Chapter 1. The All-Pair LCS Algorithm

Our starting point is to consider the generalization of above problem. Consider the following problem:

• Given a sequence of length , of length , and queries , compute the length of Longest Common Subsequence of and .

Indeed, this is the generalization of the range LIS problem. By using coordinate compression on the pair , we can assume the sequence to be a permutation of length . The LIS of the permutation is equivalent to the LCS of and sequence . Hence, if we initialize with , we obtain a data structure for LIS query.

The All-Pair LCS problem can be a problem of independent interest. For example, it has already appeared in an old Petrozavodsk contest, and there is a various solution solving the problem in time complexity (assuming ). Personally, I solved this problem by modifying the Cyclic LCS algorithm by Andy Nguyen. However, there is one particular solution which can be improved to a near-linear Range LIS solution, which is from the paper An all-substrings common subsequence algorithm.

Consider the DP table used in the standard solution of LCS problem. The states and transition forms a directed acyclic graph (DAG) over a grid graph. Explicitly, the graph consists of:

• vertices corresponding to states
• Edge of weight from to and
• Edge of weight from to if .
  

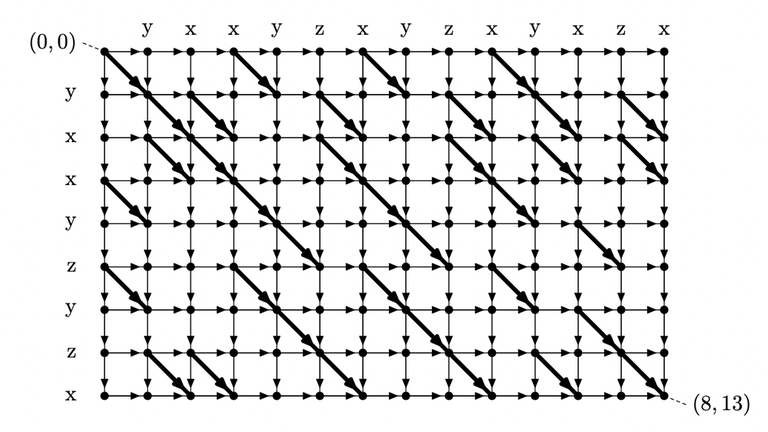
Figure: DAG constructed from the string "yxxyzyzx", "yxxyzxyzxyxzx"

Here, you can observe that the answer to the query corresponds to a longest path from to . Let's denote the length of longest path from to as . Our goal is to compute for all .

How can we do this? We need several lemmas:

Lemma 1. is either or .

Proof.

• since otherwise we can extend the path to with rightward edges.
• since we can cut the path to exactly at the column and move downward.

Lemma 2. is either or .

Proof. Identical with Lemma 1.

Lemma 3. For every , there exists some integer such that

• for all
• for all

Proof. Above statement is equivalent of following: For all we have . Consider two optimal paths from and . Since the DAG is planar, two paths always intersect. By swapping the destination in the intersection, we obtain two paths and which can not be better than optimal. Therefore we have which is exactly what we want to prove.

Lemma 4. For every , there exists some integer such that

• for all
• for all

Proof. Identical with Lemma 3.

Suppose we have the answer and for all . How can we compute the value ? Let's write it down:

It turns out that we don't even need all values, we only have to know a single linear array ! Given that we have an array , the queries can be easily answered in time with Fenwick trees, or time if we use precomputation.

Hence, all we need to do is to compute the values and , and it turns out there is a very simple recurrence.

Theorem 5. The following holds:

• For and
• For and

Proof. Base cases are trivial. For a fixed , consider the distance from to the four cells in the rectangle . Let , then the other two cells either attain value or . Therefore, the possibilities are:

• having value or (equivalently, )
• having value or (equivalently, )
• Whether or not

Those three values uniquely determine . You can verify the Theorem 5 by manually inspecting all cases by hand.

Remark. At least this is the proof I found, and this is also the proof from the original paper. I believe there is a simpler interpretation, so please add a comment if you have a good idea!

As Theorem 5 gives a simple recurrence to compute all values and , we can solve the All-Pair LCS problem in time, hence the Range LIS problem in time.

As long as SETH Conjecture is true, the longest common subsequence of two strings can not be computed faster than time. Hence our algorithm has no room for improvement. However, in the case of LIS, one of our pattern is fixed as , and it turns out we can use this to improve the time complexity.

Chapter 2. The Seaweed

Visualizing the above DP procedure gives a further insight on the structure. We can consider the value and to be associated with the edges of the grid: In that sense, the DP transition is about picking the values from the upper/left edges, and routing them to the lower/right edges of the rectangular cell. For example, we can draw a following picture:

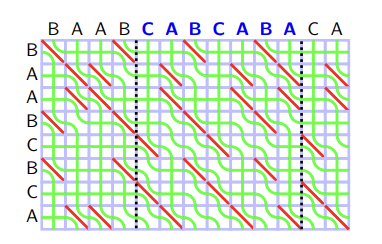
In this picture, green curves represent the values — values from the left edges of big rectangle ("BAABCBCA") are , from the upper edges of big rectangle ("BAABCABCABA") are . We will call each green curve as a seaweed. We will also read the seaweed from the lower left corner to the upper right corner, and say the seaweed is in left or right according to this order. In this regard, in the beginning seaweeds are sorted in the increasing order.

Let's reinterpret the DP transition from Theorem 5 with this visualization. If , two seaweed do not intersect. If , two seaweed intersect if the right seaweed have a greater value than the left one. In other words, each cell is the anti-sorter of seaweed: If two adjacent seaweeds have increasing values (), it swaps so that they have decreasing values ().

Of course, in the case of Range LIS we have such pair, so this is still not enough to solve the problem, but now I can present a main idea for optimization.

Suppose that we swap two values regardless of their values. We can represent each operation as a permutation where stores the final position of -th seaweed from the beginning. Let's say we have a swap operation in position , and let the elementary permutation be

Then the total operation can be described as a single permutation where is a composite permutation: .

We can't use this to solve the Range LIS problem because we take the values into account. But very surprisingly, even with that condition, there exists a cool operator such that:

• is associative.
• The total operation can be described as a single permutation

Chapter 3. The Operator

The definition of this operator is pretty unintuitive, and needs several auxiliary lemmas:

Definition 6. Given a permutation of length , let be the square matrix, such that

Intuitively, it is a partial sum in left-down direction, for example, if , we have:

Which is the partial sum of .

Definition 7. Given two matrix of size , of size , the min-plus multiplication is .

Theorem 8. Given two permutation of length , there exists a permutation of length such that . We denote such as .

To prove it we need two lemmas:

Lemma 8.1. For a matrix , there exists a permutation if and only if the following conditions are satisfied:

Proof of Lemma 8.1. Consider the inverse operation of partial sums. We can always restore the permutation if the "inverse partial sum" of each row and column contains exactly one for each rows and columns, and for all other entries. Fifth term guarantees that the elements are nonnegative, third and fourth term guarantees that each rows and columns sums to . Those conditions are sufficient to guarantee that the inverse yields a permutation.

Lemma 8.2. For any matrix , for all if and only if for all .

Proof of Lemma 8.2. is done by induction. is trivial.

Proof of Theorem 8. We will prove the first four points of Lemma 9. Note that all entries of are nonnegative since does.

• . Considering the derivative, the term is minimized when .
• . Considering the derivative, the term is minimized when .

Here, when we consider the derivative, we use the fact that . definitely decreases by when we increase the , but never increases more than even when we increase the . Therefore, it does not hurt to increase the . We will use this technique later on.

To prove the final point, let be the index where , . Suppose , we have

(Note that Lemma 8.2 is used in )

In the case of we proceed identically, this time using the Lemma 8.2 for .

Theorem 9. The operator is associative.

Proof. Min-plus matrix multiplication is associative just like normal matrix multiplication.

Lemma 10. Let be the identity permutation (), we have (For proof you can consider the derivative.)

And now here comes the final theorem which shows the equivalence of the "Seaweed" and the "Operator":

Theorem 11. Consider the sequence of seaweed and sequence of operation , where each operation denotes the following:

• In the beginning, there is -th seaweed in -th position.
• For each , we swap the seaweed in th position and th position, only if the seaweed has smaller index than seaweed .

Let be the elementary permutation as defined above. Let . Then after the end of all operation, -th seaweed is in the -th position.

Proof of Theorem 11. We will use induction over . By induction hypothesis correctly denotes the position of seaweeds after operations. Let

It suffices to prove that

• for all other if

Which is also equivalent to:

• otherwise.

Observe that has only one nonzero entry . Since we know , and only differs in the -th column. For the -th column, note that

(derivative)

If , we have

Which you can verify iff

If , we have

Which you can verify

Yes, this is a complete magic :) If anyone have good intuition for this result, please let me know in comments. (The original paper mention some group theory stuffs, but I have literally zero knowledge on group theory, and I'm also skeptical on how it helps giving intuition)

What's next

We learned all the basic theories to tackle the problem, and obtained an algorithm for the Range LIS problem. Using all the facts, we can:

• Implement the operator in time
• Use the operator for time

Hence we have... time algorithm. Of course this is very slow, but in the next article we will show how to optimize this algorithm to . We will also briefly discuss the application of this technique.

Practice problem