多项式 I：拉格朗日插值与快速傅里叶变换 - qAlex_Weiq

1. 复数和单位根

前置知识：弧度制，三角函数。

1.1 复数的引入

跳出实数域 RR，我们定义 i2=−1i2=−1，即 i=−1−−−√i=−1，并在此基础上定义 复数 a+bia+bi，其中将 b≠0b≠0 的称为 虚数。复数域记为 CC。

像这种从 aa 变成 a+bxa+bx 的 扩域 操作并不少见，例如初中学习 “平方根” 时，经常用 a+bx−−√(x>0)a+bx(x>0) 表示一个数。这类数的加减乘都是容易的，除法即考虑平方差公式 (c+dx−−√)(c−dx−−√)=c2−d2x(c+dx)(c−dx)=c2−d2x，因此 a+bx√c+dx√=(ac−bdx)+(bc−ad)x√c2−d2xa+bxc+dx=(ac−bdx)+(bc−ad)xc2−d2x。

将 xx 替换为 −1−1，复数四则运算可由实数四则运算结合 ii 的定义直接推广得到。

• 加法：(a+bi)+(c+di)=(a+c)+(b+d)i(a+bi)+(c+di)=(a+c)+(b+d)i。
• 减法：(a+bi)−(c+di)=(a−c)+(b−d)i(a+bi)−(c+di)=(a−c)+(b−d)i。
• 乘法：(a+bi)(c+di)=(ac−bd)+(ad+bc)i(a+bi)(c+di)=(ac−bd)+(ad+bc)i。
• 除法：a+bic+di=(a+bi)(c−di)(c+di)(c−di)=ac+bdc2+d2+bc−adc2+d2ia+bic+di=(a+bi)(c−di)(c+di)(c−di)=ac+bdc2+d2+bc−adc2+d2i。

1.2 复平面与棣莫弗定理

描述一个复数 a+bia+bi 需要两个值 aa 和 bb，其中 aa 表示 实部，bb 表示 虚部。这启发我们将其放在平面直角坐标系上描述，称为 复平面。其在复平面上的坐标为 (a,b)(a,b)，实部 aa 为横坐标，虚部 bb 为纵坐标。

一个复数唯一对应一个平面向量，因为它们都可以用有序实数对描述。将向量起点平移至原点，则其终点指向与其对应的复数。考虑平面向量的一些特征，如其长度与所在直线斜率。将这些概念应用在复数上，我们得到如下定义：

• 定义复数 z=a+biz=a+bi 的 模 为 |z|=a2+b2−−−−−−√|z|=a2+b2。
• 定义复数 z=a+biz=a+bi 的 辐角 为 Argz=θArg⁡z=θ，其中 tanθ=batan⁡θ=ba。满足 −π<θ≤π−π<θ≤π 的 θθ 称为 辐角主值，记作 argzarg⁡z，即 argz=arctanbaarg⁡z=arctan⁡ba。
• 辐角确定了 zz 所在直线，模确定了 zz 在直线上的长度。对比实部和虚部，模和辐角主值以另一种有序实数对的形式描述复数。

根据 z=a+biz=a+bi 的模 rr 和辐角 θθ，可知 zz 的实部 a=rcosθa=rcos⁡θ，虚部 b=rsinθb=rsin⁡θ，据此定义复数的 三角形式 z=r(cosθ+isinθ)z=r(cos⁡θ+isin⁡θ)。

利用 coscos 和 sinsin 的和角公式可得 z1z2=r1r2(cos(θ1+θ2)+isin(θ1+θ2))z1z2=r1r2(cos⁡(θ1+θ2)+isin⁡(θ1+θ2))。该等式称为 棣莫弗定理，它说明 复数相乘，模长相乘，辐角相加。

• 根据棣莫弗定理，我们得到对虚数单位 ii 的一种直观理解：将一个复数 zz 乘以 ii 相当于将其 逆时针旋转 π2π2 弧度。实际上，考虑虚数单位 ii 本身在复平面上的位置，发现就是 11 逆时针旋转 π2π2 度。一般地，有旋转的地方就有 ii 存在，ii 即旋转。推荐观看：虚数的来源 - Veritasium。

1.3 单位根的定义

当 r=1r=1 时，z=cosθ+isinθz=cos⁡θ+isin⁡θ 在单位圆上。此时根据棣莫弗公式有 zn=cos(nθ)+sin(nθ)zn=cos⁡(nθ)+sin⁡(nθ)，它在 复数旋转 和 复数乘法 之间构建了桥梁：zz 的 nn 次幂相当于从 (1,0)(1,0) 开始，以 zz 的角度在单位圆上旋转 nn 次得到的结果，称为将 zz 旋转 nn 次。

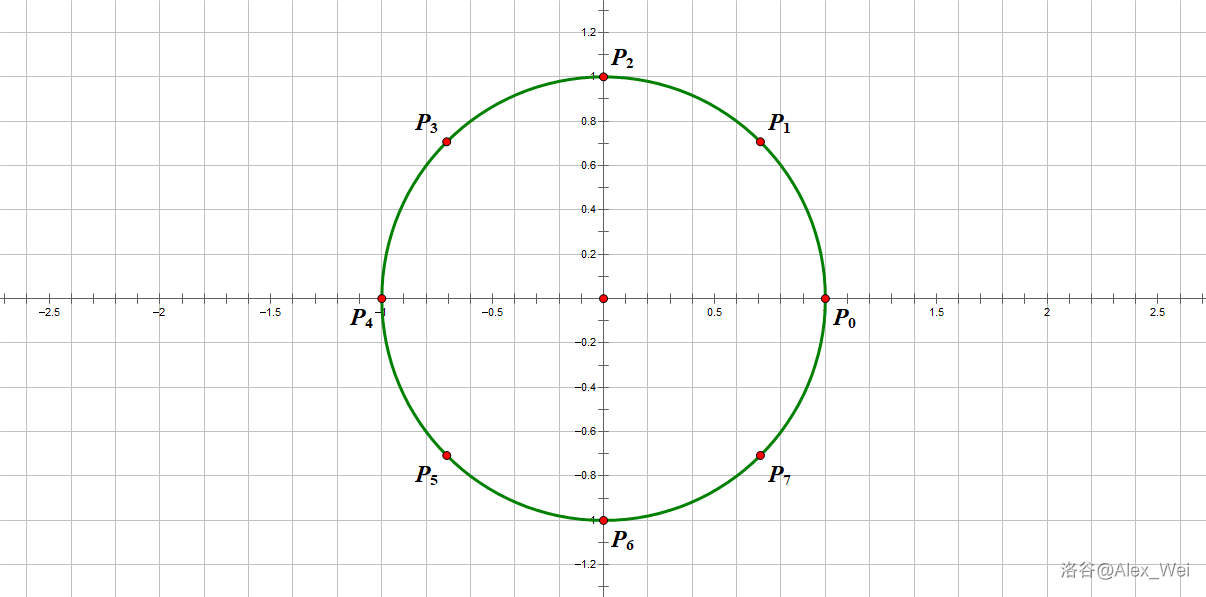
考虑将单位圆 nn 等分（如下图），取任意 nn 等分点 Pk(0≤k<n)Pk(0≤k<n)，将其旋转 nn 次均得到 11，因为跨过的 1n1n 单位圆弧数为 nn 的倍数。这说明 Pnk=1Pkn=1。

探究 PkPk 的表达式：因为它相当于从 11 开始在单位圆上旋转 2kπn2kπn 弧度，因此 Pk=cos(2kπn)+sin(2kπn)Pk=cos⁡(2kπn)+sin⁡(2kπn)。我们称所有 PkPk 为 nn 次 单位根，将 P1P1 记作 ωnωn，则 Pk=Pk1=ωknPk=P1k=ωnk。

根据 Pnk=1Pkn=1 可知任意 nn 次单位根 ωknωnk 均为 xn−1=0xn−1=0 的解。除特殊说明外，一般 nn 次单位根直接代指 ωnωn，即从 11 开始逆时针方向的第一个单位根。

可以观看 3b1b 的视频 从 6:00 到 7:30 的部分加深对上述内容的理解。

• 单位根的循环性：由 ωnn=1ωnn=1 单位根的指数可对 nn 取模。换言之，考虑从 11 开始不断乘以 ωnωn，我们将得到 1,ωn,ω2n,⋯,ωn−1n,ωnn=1,ωn+1n=ωn,⋯1,ωn,ωn2,⋯,ωnn−1,ωnn=1,ωnn+1=ωn,⋯，循环节为 nn。想象从 11 开始不断旋转 2πn2πn 弧度，旋转 nn 次后我们将落入循环。换言之，ωkn=ωk+tnn(t∈Z)ωnk=ωnk+tn(t∈Z)。
• ωkn=ωckcn(c>0)ωnk=ωcnck(c>0)。对单位根有可视化认知后容易理解这一点。
• 当 nn 为偶数时，将 ωknωnk 取反相当于将其逆时针（或顺时针）转半圈，所以 −ωkn=ωk±n2n(2∣n)−ωnk=ωnk±n2(2∣n)。
• 单位根的对称性：因为 nn 次单位根将单位圆 nn 等分，均匀分布在圆周，所以它们的重心就在原点，即 ∑n−1i=0ωin=0∑i=0n−1ωni=0。
• 若 gcd(k,n)=1gcd(k,n)=1，则 ωknωnk 称为 本原单位根。所有本原单位根的 0∼n−10∼n−1 次幂互不相同。

1.4 单位根与原根

前置知识：原根，详见 初等数论学习笔记 I：同余相关。

单位根和原根有极大的相似性，可以说原根就是模 PP 下的整数域的单位根。

设 n=φ(P)n=φ(P) 且 PP 存在原根 gg，则 g0,g1,⋯,gn−1,gn=g0,gn+1=g1g0,g1,⋯,gn−1,gn=g0,gn+1=g1 这样的循环和 nn 次单位根的循环一模一样。这使得在模 PP 意义下涉及 nn 次单位根运算时，可直接用原根 gg 代替。进一步地，对于 d∣nd∣n，gndgnd 可直接代替模 PP 意义下的 dd 次单位根。

• 单位根和原根都是对应域上一个大小为 n=φ(P)n=φ(P) 的 循环群 的 生成元。它们均满足 nn 次幂是对应域的单位元，且它们的 0∼n−10∼n−1 次幂互不相同。换言之，它们 同构。

快速傅里叶变换 FFT 和快速数论变换 NTT 的联系恰在于此。

1.5 欧拉公式

前置知识：自然对数 lnln 的底数 ee 及其相关性质。

这部分为接下来可能用到的符号做一些补充。

欧拉公式指出

即单位圆上从 (1,0)(1,0) 开始旋转 xx 弧度得到的复数，也即大小为 xx 的角的终边与单位圆的交点。

欧拉公式的严谨证明超出了讨论范围，相关资料可以参考百度百科。我们给出一个对欧拉公式的感性理解方式，以加深读者对欧拉公式的直观印象与理解，来自 在 3.14 分钟内理解 eiπeiπ - 3Blue1Brown。这个视频相当有启发性。

根据 (et)′=et(et)′=et，考虑 etet 随着 tt 增大在数轴上的取值。etet 以每秒钟 tt 均匀增加 11 的速度向数轴正方向移动，则 etet 的速度就是它本身的位置。它的起始点为 e0=1e0=1。

根据 (ekt)′=ket(ekt)′=ket，类似可知 ektekt 的速度等于 kk 倍它本身的位置。

当 k=ik=i 时，速度相当于将本身的位置逆时针旋转 π2π2 弧度，与位置垂直。这样，根据基础的高中物理知识，我们知道 eiteit 随着 tt 增大，在单位圆上做匀速圆周运动，且每秒移动 11 弧度。

这样，eiteit 就等于模长为 11，辐角为 tt 的复数，即 cost+isintcos⁡t+isin⁡t。这使得我们可以用 reiθreiθ 描述模长为 rr，辐角为 θθ 的复数，记号变得更简洁。

将该表示法应用至单位根，可知 ωn=e2πinωn=e2πin。

读者应当在 reiθreiθ，r(cosθ+isinθ)r(cos⁡θ+isin⁡θ) 及其在复平面上的位置建立直观联系，有助于理解接下来的内容。

带入 t=πt=π，得到著名等式

带入 t=2π=τt=2π=τ，得

这说明对于任意 k∈Zk∈Z，(e2πi)k+tn(e2πi)k+tn 相等恰对应 ωkn+tnωnkn+t 相等。

2. 多项式

2.1 基本概念

形如 ∑ni=0aixi∑i=0naixi 的 有限和式 称为 多项式，记作 f(x)=∑ni=0aixif(x)=∑i=0naixi。其中，aiai 称为 ii 次项的 系数，也称 xixi 前的系数，记作 [xi]f(x)[xi]f(x)。超出最高次数 nn 的系数 ai(i>n)ai(i>n) 视作 00。

当项数无限时，和式形如 ∑∞i=0aixi∑i=0∞aixi，称为 形式幂级数，它暂时超出了我们的讨论范围。

• 多项式 系数非零 的最高次项的次数称为该多项式的 度，也称次数，记作 degfdeg⁡f。如 f(x)=∑ni=0aixif(x)=∑i=0naixi 其中 an≠0an≠0，则 ff 为 nn 次多项式，记作 degf=ndeg⁡f=n。
• 使得 f(x)=0f(x)=0 的所有 xx 称为多项式的 根。
• 若 aiai 均为实数，则称 ff 为实系数多项式。若 aiai 可以均为复数，则称 ff 为复系数多项式。
• 代数基本定理：任何非零一元 nn 次复系数多项式恰有 nn 个复数根。这些复数根可能重合。证明略。

2.2 系数表示法和点值表示法

f(x)=∑ni=0aixif(x)=∑i=0naixi 给出了所有 ii 次项前的系数，这种描述多项式的方法称为 系数表示法。

将 x=xix=xi 带入，得到 yi=f(xi)yi=f(xi)，称 (xi,yi)(xi,yi) 为 ff 在 xixi 处的点值。用若干点值 (xi,yi)(xi,yi) 描述多项式的方法称为 点值表示法。

考虑这两种表示法之间的联系。我们尝试探究在给定 nn 个点值 (x0,y0),(x1,y1),⋯,(xn−1,yn−1)(x0,y0),(x1,y1),⋯,(xn−1,yn−1) 其中 xixi 互不相同时，所唯一确定的多项式的最高次数。

一个自然的猜测是 n−1n−1，因为 n−1n−1 次多项式需要 nn 个系数描述，具有 nn 单位信息，而 nn 个点值同样具有 nn 单位信息。

证明即考虑直接带入，得到 nn 元线性方程组：对于任意 0≤j<n0≤j<n，∑n−1i=0aixij=yj∑i=0n−1aixji=yj。该线性方程组的系数矩阵为

因 xixi 互不相同，所以该范德蒙德矩阵的行列式非零，方程组有唯一解。类似的，从线性方程组的角度出发，容易证明 nn 个点值不可能唯一确定 nn 次或更高次的多项式。

综上，我们得到重要结论：nn 个点值唯一确定的多项式最高次数为 n−1n−1。

• 从系数表示法转为点值表示法称为 求值（Evaluation）。
• 从点值表示法转为系数表示法称为 插值（Interpolation）。

2.3 多项式运算

2.3.1 基本运算

设 f(x)=∑ni=0aixif(x)=∑i=0naixi，g(x)=∑mi=0bixig(x)=∑i=0mbixi。

• 设 h=f+gh=f+g，则 h(x)=(∑ni=0aixi)+(∑mj=0bjxj)=∑max(n,m)i=0(ai+bi)xih(x)=(∑i=0naixi)+(∑j=0mbjxj)=∑i=0max(n,m)(ai+bi)xi，可知两多项式相加，对应系数相加，deg(f+g)=max(degf,degg)deg⁡(f+g)=max(deg⁡f,deg⁡g)。
• 设 h=f∗gh=f∗g，则 h(x)=(∑ni=0aixi)(∑mj=0bjxj)=∑n+mi=0(∑ij=0ajbi−j)xih(x)=(∑i=0naixi)(∑j=0mbjxj)=∑i=0n+m(∑j=0iajbi−j)xi，可知两多项式相乘，每两个系数相乘贡献至次数之和的系数，deg(f∗g)=degf+deggdeg⁡(f∗g)=deg⁡f+deg⁡g。

因此，在系数表示法下，计算两个多项式相加的复杂度为 O(n+m)O(n+m)，计算两个多项式相乘的复杂度为 O(nm)O(nm)。

• 根据 (f+g)(x)=f(x)+g(x)(f+g)(x)=f(x)+g(x)，可知两个多项式相加时，对应点值相加。

• 根据 (fg)(x)=f(x)g(x)(fg)(x)=f(x)g(x)，可知两个多项式相乘时，对应点值相乘。

因此，在点值表示法下，计算两个多项式相加需要 max(n,m)+1max(n,m)+1 个点值，计算两个多项式相乘需要 n+m+1n+m+1 个点值，复杂度均为 O(n+m)O(n+m)。

• 用 f∗gf∗g 和 fgfg 表示多项式相乘，即进行加法卷积；用 f⋅gf⋅g 表示多项式 点乘，即 对应系数相乘。

在系数表示法下计算两个多项式相乘，我们首先将其转化为点值表示法，相乘后再转回系数表示法。时间复杂度 O((n+m)log(n+m))O((n+m)log⁡(n+m))。相关算法将在第四章介绍。

3. 拉格朗日插值

在 2.2 小节我们得到结论：nn 个点值唯一确定的多项式最高次数为 n−1n−1。那么，如何在点值表示法和系数表示法之间快速转换呢？

从系数表示法转为点值表示法，最常用的方法是直接带入，时间复杂度 O(n2)O(n2)。O(nlog2n)O(nlog2⁡n) 的多项式多点求值则需要高级多项式技巧，此处不作介绍。

从点值表示法转为系数表示法，最直接的方法是高斯消元，时间复杂度 O(n3)O(n3)。接下来我们将介绍常用的拉格朗日插值法。

3.1 算法详解

拉格朗日插值的核心思想在于利用点值的可加性，每次只考虑一个点值，其它点值均视为 00，由此构造 nn 个多项式 fi(x)fi(x)，使得它们在 xixi 处取值为 yiyi，xj(j≠i)xj(j≠i) 处取值为 00，则 f=∑n−1i=0fif=∑i=0n−1fi。中国剩余定理 使用了类似的思想。

为了让 fi(xj)=0 (i≠j)fi(xj)=0(i≠j)，fifi 应包含 x−xjx−xj 作为因式，因此设 fi(x)=∏i≠j(x−xj)fi(x)=∏i≠j(x−xj)。但是此时 fi(xi)fi(xi) 不一定等于 yiyi，我们发现可以调整 fifi 的系数，给 fifi 乘上 yifi(xi)yifi(xi)。综上，我们得到 fifi 的表达式

对 fifi 求和得 ff，我们得到拉格朗日插值公式

为得到 ff 的各项系数，只需 O(n2)O(n2) 求出 F(x)=∏n−1i=0(x−xi)F(x)=∏i=0n−1(x−xi)，对每个 ii 暴力 O(n)O(n) 将 FF 除掉一次式 x−xix−xi 算出 F(x)x−xiF(x)x−xi 的各项系数，再乘以 yi∏j≠ixi−xjyi∏j≠ixi−xj 得到 fifi，则 f=∑n−1i=0fif=∑i=0n−1fi。时间复杂度 O(n2)O(n2)。

通常情况下，题目要求我们求出 F(x)F(x) 在给定某个 xx 处的取值，此时我们不把 xx 看做函数的元，而是直接将 xx 带入上式。时间复杂度仍为 O(n2)O(n2)。

多项式快速插值在 O(nlog2n)O(nlog2⁡n) 的时间内将点值表示法转化为系数表示法，这超出了我们的讨论范围。

3.2 连续取值插值

当给定点值横坐标为连续整数时，我们有快速单点插值的方法。

以 0,1,⋯,n−10,1,⋯,n−1 即 xi=ixi=i 为例：

分子是 ∏(x−i)∏(x−i) 挖掉一个项，经典维护前缀后缀积。设 pi=∏i−1j=0x−jpi=∏j=0i−1x−j，si=∏n−1j=i+1x−jsi=∏j=i+1n−1x−j。

分母对于 i>ji>j，∏i−1j=0(i−j)=i!∏j=0i−1(i−j)=i!。对于 i<ji<j，∏n−1j=i+1(i−j)=(−1)(−2)⋯(i−n+1)∏j=i+1n−1(i−j)=(−1)(−2)⋯(i−n+1)，将所有负号提出来，得 (−1)n−i+1(i−n+1)!(−1)n−i+1(i−n+1)!。

预处理阶乘逆元，时间复杂度 O(n)O(n)。

3.3 应用

• 计算范德蒙德方阵的逆矩阵，详见 4.4.1 小节。

3.4 例题

P4781 【模板】拉格朗日插值

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e3 + 5;
constexpr int mod = 998244353;
int ksm(int a, int b) {
  int s = 1;
  while(b) {
    if(b & 1) s = 1ll * s * a % mod;
    a = 1ll * a * a % mod, b >>= 1;
  }
  return s;
}
int n, k, ans, x[N], y[N];
int main() {
  cin >> n >> k;
  for(int i = 1; i <= n; i++) cin >> x[i] >> y[i];
  for(int i = 1; i <= n; i++) {
    int deno = 1, nume = 1;
    for(int j = 1; j <= n; j++) {
      if(i == j) continue;
      deno = 1ll * deno * (x[i] + mod - x[j]) % mod;
      nume = 1ll * nume * (k + mod - x[j]) % mod;
    }
    ans = (ans + 1ll * y[i] * nume % mod * ksm(deno, mod - 2)) % mod;
  }
  cout << ans << "\n";
  return 0;
}

4. 快速傅里叶变换

快速傅里叶变换（Fast Fourier Transform，FFT）是多项式算法的根基。想要真正理解它，必须先真正理解单位根，还需要对线性代数有基本了解。

推荐观看：

4.1 求值的本质

设 f(x)=∑n−1i=0aixif(x)=∑i=0n−1aixi，将 x0x0 带入，得 f(x0)=∑n−1i=0aixi0f(x0)=∑i=0n−1aix0i。考虑将其写成向量内积（点积）的形式：

这样，如果有 x0,x1,⋯,xm−1x0,x1,⋯,xm−1 需要求值，整个过程就可以写成 m×nm×n 维矩阵乘以 nn 维列向量的形式：

左侧矩阵就是著名的 范德蒙德矩阵。

当 m=nm=n 时为范德蒙德方阵，xixi 互不相同时其逆存在，帮助我们快速从点值表示法转回系数表示法。m>nm>n 时任取 xixi 互不相同的 n+1n+1 行可以求逆。m<nm<n 时无法还原系数。这体现出 n+1n+1 个点值唯一确定最高次数不超过 nn 的多项式。

朴素计算求值的复杂度为 O(nm)O(nm)，因为带入求值一次的复杂度为 O(n)O(n)。快速傅里叶变换即在离散傅里叶变换基础上通过选取合适的 xixi，使得可以快速求值。

4.2 离散傅里叶变换

在介绍 FFT 之前，我们先给出离散傅里叶变换（Discrete Fourier Transform，DFT）的概念。

DFT 在工程中是将离散信号从时域转为频域的过程。碰巧的是，其表达式刚好可以用来对多项式进行多点求值，只不过这些点值是固定的 单位根 处的点值，但对于求值做多项式乘法已经足够了。

DFT 将一个长度为 NN 的复数序列 x0,x1,⋯,xN−1x0,x1,⋯,xN−1 通过如下公式转化为另一个长为 NN 的复数序列 X0,X1,⋯,XN−1X0,X1,⋯,XN−1：

设多项式 f(x)=∑N−1n=0xnxif(x)=∑n=0N−1xnxi，易知

根据上式，离散傅里叶变换可以看成多项式 f(x)=∑N−1n=0xnxif(x)=∑n=0N−1xnxi 在 NN 个单位根处求值。

没看懂？没关系。接下来我们将从另一角度出发，得到一个差别微小但更容易理解的算法 —— FFT。

4.3 算法详解

首先我们得搞清楚，DFT 是一个变换，而 FFT 是用于实现 DFT 的算法。在 FFT 的推导过程中，其所实现的变换和 DFT 变换有细微的差别，因此笔者也用 FFT 表示该算法实现的变换。

按理说学习一个算法时需要搞清楚它的用途，但如果直接从 DFT 角度入手尝试简化流程，那么为了让动机看起来自然，我们还要先学习 DFT 的实际含义，这涉及到大量前置知识。

但是，从计算机科学界尤为重要且为各位 OIer 熟知的多项式乘法的优化出发，我们通过自然推理得到一个算法，而该算法恰好可以快速实现 DFT（有一些细小的差别，详见 4.3.5）。

我们明确接下来的目标：给定次数 n−1n−1 的多项式 f(x)=∑n−1i=0aixi(an−1≠0)f(x)=∑i=0n−1aixi(an−1≠0)，快速求出它的至少 nn 个点值。

下文中，f(x)f(x) 也被视为关于 xx 的 n−1n−1 次函数。

4.3.1 简化情况

解决一个普遍性的问题，最重要的思想就是 从简化情况入手，分析问题的性质。

函数的性质无非就那几个：奇偶性，单调性，周期性等。一般函数没有单调性和周期性，但总可以表示为一个偶函数和一个奇函数之和，这一定是突破点。

• 对于偶函数 f(x)f(x)，即所有奇数次项系数为 00，带入两个相反数 ww 和 −w−w 时，它们的值相等。

• 对于奇函数 f(x)f(x)，即所有偶数次项系数为 00，带入两个相反数 ww 和 −w−w 时，它们的值互为相反数。

因此，将任意多项式 f(x)f(x) 拆成偶函数 fe(x)fe(x) 和奇函数 fo(x)fo(x) 之和，则

选择 ⌈n2⌉⌈n2⌉ 对两两互为相反数的值 (xi,−xi)(xi,−xi) ，求出所有 xixi 在 fe(x)fe(x) 和 fo(x)fo(x) 处的取值。

不妨设 nn 为偶数，则 fefe 是 n−2n−2 次多项式，fefe 是 n−1n−1 次多项式，本质上依然相当于求出 n−1n−1 次多项式的 nn 个点值，对时间复杂度没有优化。

但是 fefe 和 fofo 的项数减半，尝试利用该性质。

因为 fefe 只有偶数次项 a0x0+a2x2+⋯a0x0+a2x2+⋯，故考虑换元 u=x2u=x2，则 fe(u)=a0u0+a2u1+⋯fe(u)=a0u0+a2u1+⋯。换言之，我们设 f′e(x)=a0x0+a2x1+⋯fe′(x)=a0x0+a2x1+⋯，则 fe(x)=f′e(x2)fe(x)=fe′(x2)。

同理，从 fofo 中提出一个 xx，设 f′o(x)=a1x0+a3x1+⋯fo′(x)=a1x0+a3x1+⋯，则 fo(x)=xf′o(x2)fo(x)=xfo′(x2)。

这样才是真正意义上的规模减半。若问题可递归，则时间复杂度为 T(n)=2T(n2)+O(n)T(n)=2T(n2)+O(n)，解得 T(n)=O(nlogn)T(n)=O(nlog⁡n)。

4.3.2 引入单位根

问题来了，如何保证递归得到的问题也满足两两互为相反数呢？

考虑一开始的 (xi,−xi)(xi,−xi)，这说明存在 i′i′ 使得 x2i=−x2i′xi2=−xi′2，它们互不相同但它们的 44 次方相等。

进一步推演，因为问题会递归 w=⌈log2n⌉w=⌈log2⁡n⌉ 层，所以我们需要找到 k=2wk=2w 个互不相等的 xx，但它们的 kk 次幂相等。这个相等的 kk 次幂可以任意选择，方便起见设为 11，则 xk=1xk=1，xx 为所有 kk 次单位根。

逆推得到结果后，我们再顺着检查一遍：初始令 xx 为所有 kk 次单位根，每层递归会将这些数平方，得到所有 k2,k4⋯k2,k4⋯ 次单位根。因为 k2,k4,⋯k2,k4,⋯ 都是偶数，所以它们可以两两正负配对，直到递归 ww 层的平凡情况：k2w=1k2w=1 次单位根即 x=1x=1。

由此可得通常使用（补齐到 22 的幂）的快速傅里叶变换的范德蒙德方阵形式：

4.3.3 递归公式

得到大致框架后，我们具体地描述整个算法流程：

首先将 nn 补齐到不小于 nn 的最小的 22 的幂，即 2⌈log2n⌉2⌈log2⁡n⌉。

设当前需要求值的多项式 ff 长度为 L(L=2w,w∈N)L(L=2w,w∈N)，若 L=1L=1 则直接返回 a0a0。否则我们需求出 f(x)f(x) 在所有 LL 次单位根 ωkL(0≤k<L)ωLk(0≤k<L) 处的取值。

将 f(x)f(x) 写成 fe(x2)+xfo(x2)fe(x2)+xfo(x2)，则对于 0≤k<L20≤k<L2，有

根据单位根的性质（在单位根部分有介绍）：

• ωkn=ω2k2nωnk=ω2n2k。
• ωkn=ωk+tnn(t∈Z)ωnk=ωnk+tn(t∈Z)。
• ωkn=−ωk+n2n(2∣n)ωnk=−ωnk+n2(2∣n)。

这样，我们只需求出 L2L2 次多项式 fefe 和 fofo 在所有 L2L2 次单位根处的取值。

4.3.4 蝴蝶变换

递归处理比较慢，我们希望像位运算卷积一样通过递推实现整个过程。

因为在边界条件下，每个位置的取值与其对应的系数相关，所以递归转递推的关键在于考察系数的变化。

考虑 n=8n=8 的情况，初始为 (a0,a1,a2,a3,a4,a5,a6,a7)(a0,a1,a2,a3,a4,a5,a6,a7)。

进行第一层递归时，将 fefe 的系数写在左半部分，fofo 的系数写在右半部分，得 (a0,a2,a4,a6),(a1,a3,a5,a7)(a0,a2,a4,a6),(a1,a3,a5,a7)。

进行第二层递归时，类似地将每个子问题的 fefe 和 fofo 的系数分别写在左右两侧，得 (a0,a4),(a2,a6),(a1,a5),(a3,a7)(a0,a4),(a2,a6),(a1,a5),(a3,a7)。

进行第三层递归时，共有 44 个大小为 22 的子问题，且进行上述操作后系数的位置不发生改变。

我们看到，如果一个系数在规模为 2n2n 的问题中的位置为 pp，若 pp 是偶数，则递归至左半部分，若 pp 是奇数，则递归至右半部分，且在规模为 nn 的问题中的位置为 ⌊p2⌋⌊p2⌋。

进一步地，一个系数在第 ii 次递归时的方向决定了它最终下标在二进制下第 w−i(n=2w)w−i(n=2w) 位的取值。若向左递归则为 00，向右递归则为 11。而它递归的方向又受到 ⌊p2i−1⌋⌊p2i−1⌋ 的奇偶性的影响，即 pp 在二进制下第 ii 位的取值，若为 00 则向左递归，为 11 则向右递归。

这就说明，pp 在二进制下第 ii 位的取值，等于它对应的系数的最终下标在二进制下第 w−iw−i 位的取值。

因此我们断言，系数 apap 在 ww 次递归后的下标等于 pp 二进制翻转后的值，设为 rprp。这里翻转指翻转第 0∼w−10∼w−1 位的值。

rprp 可递推求得：r0=0r0=0。对于 ri(i>0)ri(i>0)，先右移一位得到 i′=⌊i2⌋i′=⌊i2⌋，则 riri 的低 w−1w−1 位（第 0∼w−20∼w−2 位）的值可由 ri′ri′ 右移一位得到。第 w−1w−1 位的值只需检查 ii 的奇偶性。因此，ri=⌊ri′2⌋+n2(imod2)ri=⌊ri′2⌋+n2(imod2)，其中 i′=⌊i2⌋i′=⌊i2⌋。

因此，在算法一开始先对系数数组 aa 执行 蝴蝶变换，即同时令 ai→ariai→ari，然后类似 FWT，枚举问题规模 2d(1≤d<n)2d(1≤d<n)，枚举每个子问题 2di(0≤2di<n)2di(0≤2di<n)，再枚举当前子问题的所有对应位置 (x=2di+k,y=2di+k+d)(0≤k<d)(x=2di+k,y=2di+k+d)(0≤k<d) 执行变换，即设 xx 和 yy 对应位置的当前值为 fxfx 和 fyfy，则 f′x=fx+ωk2dfyfx′=fx+ω2dkfy，f′y=fx−ωk2dfyfy′=fx−ω2dkfy。

进一步地，根据 rr 的定义，我们有 rri=irri=i。因此，执行蝴蝶变换只需对所有 i<rii<ri 执行 swap(ai,ari)swap(ai,ari)。

这就是 FFT，整个过程称为 对多项式 ff 做长度为 nn 的快速傅里叶变换，时间复杂度 O(nlogn)O(nlog⁡n)。代码在 4.5 小节。

4.3.5 DFT 和 FFT

对比 DFT 和 FFT 矩阵：

可以发现 DFT 和 FFT 基本一致，它们的差别在于：

• 朴素 FFT 要求 nn 是 22 的幂，但 DFT 序列长度可以是任意正整数。
• DFT 和 FFT 带入单位根的顺序是相反的。

注意这些细微差别，不要把 DFT 和 FFT 搞混了。

4.3.6 循环卷积

4.4 离散傅里叶逆变换

离散傅里叶逆变换（Inverse Discrete Fourier Transform，IDFT）可以视为单位根处插值的过程。即给出 n=2wn=2w 个在所有 nn 次单位根处的点值 Pk=(ωkn,f(ωkn))(0≤k<n)Pk=(ωnk,f(ωnk))(0≤k<n)，要求还原 ff 的各项系数，其中 ff 的次数不大于 n−1n−1。

类似地，IDFT 和 IFFT 之间也存在一些差异。想必各位读者根据之前的内容已经可以猜出这种差异是什么了。

4.4.1 范德蒙德方阵逆

考虑范德蒙德方阵

这玩意怎么求逆？我们考虑最暴力的方法：拉格朗日插值！

因为范德蒙德方阵可以看成多项式多点求值，根据

再结合拉格朗日插值公式

可知从 f(xj)f(xj) 贡献到 aiai 的系数为 (A−1)ij=[xi]∏k≠ix−xkxj−xk(A−1)ij=[xi]∏k≠ix−xkxj−xk。

这就是范德蒙德方阵逆当中每个元素的表达式。

4.4.2 算法介绍

很显然，ff 在经过快速傅里叶变换后，再进行快速傅里叶逆变换，仍得到 ff。

因此，只需对快速傅里叶变换的矩阵求逆，即可得到快速傅里叶逆变换的矩阵。

设 ωω 表示 ωnωn，则

则 (F−1)ij=[xi]∏k≠jx−ωkωj−ωk(F−1)ij=[xi]∏k≠jx−ωkωj−ωk。

分子和分母均形如 g(x)=∏0≤k<n(x−ωk)x−ωjg(x)=∏0≤k<n(x−ωk)x−ωj，我们研究该函数的性质。

首先，因为 ωk(0≤k<n)ωk(0≤k<n) 为 xn−1=0xn−1=0 的 nn 个互不相同的根，根据因式定理，∏0≤k<n(x−ωk)∏0≤k<n(x−ωk) 就等于 xn−1xn−1。感性理解：将 ∏0≤k<n(x−ωk)∏0≤k<n(x−ωk) 展开，再应用单位根的 对称性。

模拟短除法 xn−1x−ωjxn−1x−ωj，可知

因此，对一个序列做 IFFT，只需将 FFT 递归公式里面的 ωkLωLk 换成 ω−kLωL−k，并在最后将所有数除以 nn 即可。

这就引出了 IDFT 公式及其对应矩阵：

4.5 快速多项式乘法

通过 FFT 和 IFFT，我们可以在 O(nlogn)O(nlog⁡n) 的时间内实现 n−1n−1 次多项式在系数表示法和点值表示法之间的转换。

计算两个次数分别为 n−1n−1 和 m−1m−1 的多项式 a,ba,b 相乘，设结果为 cc，则 cc 是 n+m−2n+m−2 次多项式，我们需要 n+m−1n+m−1 个点值才能确定它。根据点值的性质，首先找到不小于 n+m−1n+m−1 的最小的 22 的幂 LL，对系数表示法的 a,ba,b 分别做长度为 LL 的 FFT，将对应点值相乘得到 c^c^，再对 c^c^ 做 IFFT 还原 cc。

---

首先我们需要实现一个复数类，它支持复数的加减乘运算。也可以使用 C++ 自带复数类 std::complex<T>，用法见 CPP reference。

FFT 和 IFFT 大体上一致，只有一些细小差别。我们可以类似实现 FWT 和 IFWT 那样，用同一个函数实现它们，并用一个参数区别。

等式 ωn=cos(2πn)+isin(2πn)ωn=cos⁡(2πn)+isin⁡(2πn) 帮助我们求出 nn 次单位根。

• 注意浮点数的精度。当多项式系数的绝对值较大时，需使用 long double 甚至 5.2 小节的任意模数卷积。

模板题 P3803 代码：

#include <bits/stdc++.h>
using namespace std;

constexpr int N = 1 << 21;
constexpr double pi = acos(-1);

struct comp {
  double a, b; // a + bi
  comp operator + (const comp &x) const {return {a + x.a, b + x.b};}
  comp operator - (const comp &x) const {return {a - x.a, b - x.b};}
  comp operator * (const comp &x) const {return {a * x.a - b * x.b, a * x.b + b * x.a};}
} f[N], g[N], h[N];
int n, m, r[N];

void FFT(int L, comp *f, bool type) { // L 表示长度, type = 1 表示 FFT, type = 0 表示 IFFT
  for(int i = 1; i < L; i++) {
    r[i] = (r[i >> 1] >> 1) + (i & 1 ? L >> 1 : 0);
    if(i < r[i]) swap(f[i], f[r[i]]);
  }
  for(int d = 1; d < L; d <<= 1) {
    comp wd = {cos(pi / d), sin(pi / d)}; // 2d 次单位根
    if(!type) wd.b = -wd.b; // IFFT 单位根取倒数, 相当于沿 x 轴对称
    static comp w[N];
    w[0] = {1, 0};
    for(int j = 1; j < d; j++) w[j] = w[j - 1] * wd; // 用数组记录 0 ~ d-1 次单位根, 减少复数乘法次数
    for(int i = 0; i < L; i += d << 1) {
      for(int j = 0; j < d; j++) {
        comp x = f[i | j], y = w[j] * f[i | j | d];
        f[i | j] = x + y, f[i | j | d] = x - y;
      }
    }
  }
  if(!type) for(int i = 0; i < L; i++) f[i].a /= L; // IFFT 时所有数要除以长度 L, 我们只用到了实部所以只需将实部除以 L
}

int main() {
  cin >> n >> m;
  for(int i = 0; i <= n; i++) cin >> f[i].a;
  for(int i = 0; i <= m; i++) cin >> g[i].a;
  int L = 1;
  while(L <= n + m) L <<= 1;
  FFT(L, f, 1), FFT(L, g, 1);
  for(int i = 0; i < L; i++) h[i] = f[i] * g[i];
  FFT(L, h, 0);
  for(int i = 0; i <= n + m; i++) cout << (int) (h[i].a + 0.5) << (i < n + m ? ' ' : '\n');
  return 0;
}

4.6 快速数论变换

前置知识：原根和阶。

我们将 DFT 的数值范围从复数域推广至任意存在 nn 次单位根 αα 的环 RR，其中 αα 满足 αk(0≤k<n)αk(0≤k<n) 互不相同，对 x0,x1,⋯,xn−1x0,x1,⋯,xn−1 DFT 得 X0,X1,⋯,Xn−1X0,X1,⋯,Xn−1，则

也可以视作 Xi=f(αi)Xi=f(αi)，其中 f(t)=∑n−1j=0xjtjf(t)=∑j=0n−1xjtj。

类似可知 IDFT

即 DFT 和 IDFT 对序列进行的变换的本质抽象。

4.6.1 算法介绍

快速数论变换即在模 pp 意义下的整数域 F=Z/pF=Z/p 进行的快速傅里叶变换。

设变换长度为 nn，则需存在 nn 次单位根 aa 满足 δp(a)=nδp(a)=n。大部分题目的模数 pp 满足：

• pp 为质数。
• 2k∣p−12k∣p−1，其中 2k2k 不小于最大的可能的 NTT 长度。

第一条性质保证 pp 存在原根 gg 且 nn 可逆，第二条性质保证存在 nn 次单位根。注意它不是充要条件，只是充分条件。

根据原根的性质，δp(g)=p−1δp(g)=p−1，即 gg 的 0∼p−20∼p−2 次幂互不相同，则 gg 在 FF 上的性质和复数域上 p−1p−1 次单位根的性质完全一致：gk(0≤k<p−1)gk(0≤k<p−1) 和 ωkp−1(0≤k<p−1)ωp−1k(0≤k<p−1) 形成的域是同构的，gkgk 等价于 ωkp−1ωp−1k。

因此，q=gp−1nq=gp−1n 等价于 ωp−1np−1ωp−1p−1n 即 ωnωn，它的 0∼n−10∼n−1 次幂互不相同，即 δp(q)=nδp(q)=n，也可以通过阶的性质 δp(gk)=δp(g)gcd(δp(g),k)δp(gk)=δp(g)gcd(δp(g),k) 说明。

常见 NTT 模数有：

• 998244353=7×17×223+1998244353=7×17×223+1，有原根 33。它可以用来做长度不超过 223223 的 NTT，也是最常见的模数。
• 1004535809=479×221+11004535809=479×221+1，有原根 33。
• 469762049=7×226+1469762049=7×226+1，有原根 33。

如果不是常见模数，我们需要检验 pp 是否为形如 q2k+1q2k+1 的质数，2k2k 是否足够大，再运用原根相关的知识枚举并判定找到任意一个原根，就可以做 NTT 了。

注意以上只是模数 pp 可 NTT 的充分条件，它的更弱的条件是存在 δp(a)=nδp(a)=n 和 n−1n−1。如果 NTT 是正解的一部分，那么一个合格的出题人应将 pp 设为常见模数，因为模数不是考察重点。

4.6.2 代码实现

朴素 NTT 已经比 FFT 快了不少，因为复数运算很耗时。

接下来加入一些常数优化：

• 预处理 2d2d 次单位根的 0∼d−10∼d−1 次幂，这样对每个 ii 枚举 jj 的时候就不需要重复计算单位根的幂。
• 用 unsigned long long 和 1616 次模一次的技巧，减少取模次数。类似技巧也用于优化矩阵乘法。

综上，写出如下代码（依然是 模板题）：尽管题目没有要求取模，但可视为在模 pp 意义下进行多项式乘法，其中 pp 大于答案的每一项。

#include <bits/stdc++.h>
using namespace std;

using ull = unsigned long long;
constexpr int N = 1 << 21;
constexpr int mod = 998244353;
constexpr int ivg = (mod + 1) / 3;

int ksm(int a, int b) {
  int s = 1;
  while(b) {
    if(b & 1) s = 1ll * s * a % mod;
    a = 1ll * a * a % mod, b >>= 1;
  }
  return s;
}

int n, m, r[N], f[N], g[N], h[N];
void FFT(int L, int *a, bool type) {
  static ull f[N], w[N];
  for(int i = 0; i < L; i++) f[i] = a[r[i] = (r[i >> 1] >> 1) | (i & 1 ? L >> 1 : 0)];
  for(int d = 1; d < L; d <<= 1) {
    int wd = ksm(type ? 3 : ivg, (mod - 1) / (d + d));
    for(int j = w[0] = 1; j < d; j++) w[j] = 1ll * w[j - 1] * wd % mod;
    for(int i = 0; i < L; i += d << 1) {
      for(int j = 0; j < d; j++) {
        int y = w[j] * f[i | j | d] % mod;
        f[i | j | d] = f[i | j] + mod - y, f[i | j] += y;
      }
    }
    if(d == (1 << 16)) for(int p = 0; p < L; p++) f[p] %= mod;
  }
  int inv = ksm(L, mod - 2);
  for(int i = 0; i < L; i++) a[i] = f[i] % mod * (type ? 1 : inv) % mod;
}
int main() {
  cin >> n >> m;
  for(int i = 0; i <= n; i++) cin >> f[i];
  for(int i = 0; i <= m; i++) cin >> g[i];
  int L = 1;
  while(L <= n + m) L <<= 1;
  FFT(L, f, 1), FFT(L, g, 1);
  for(int i = 0; i < L; i++) h[i] = 1ll * f[i] * g[i] % mod;
  FFT(L, h, 0);
  for(int i = 0; i <= n + m; i++) cout << h[i] << (i < n + m ? ' ' : '\n');
  return 0;
}

5. 应用与技巧

FFT 和 NTT 是所有快速多项式操作的基础。

设多项式 ff DFT 得到 f^f^，也记为 DFT(f)DFT⁡(f)。可以发现，DFT 是线性变换，因此它具有 线性性，这是它最重要且最常用的一个性质：

• cDFT(f)+dDFT(g)=DFT(cf+dg)cDFT⁡(f)+dDFT⁡(g)=DFT⁡(cf+dg)。

5.1 常数优化

在分析变换次数的时候，一般不区分 DFT 和 IDFT。

5.1.1 三次变两次优化

计算两 实系数 多项式 f,gf,g 相乘。

根据 (a+bi)2=(a2−b2)+2abi(a+bi)2=(a2−b2)+2abi，将 f+gif+gi 平方后取出虚部再除以 22 即可。

这样，三次 DFT 变成了两次 DFT，对常数有显著优化。代码。

这个优化被接下来稍复杂的技巧完全包含，它们的核心思想都是利用实系数的性质。

5.1.2 合并两次实系数 DFT

同时计算两 实系数 多项式 f,gf,g 的 DFT。

类似地，我们设 u=f+igu=f+ig，v=f−igv=f−ig。先求出 uu 的 DFT u^u^，考虑能否利用 u^u^ 直接求出 v^v^。

在给出做法之前，我们还要引入一些复数相关的概念：

• 定义：对于两个复数 z1z1 和 z2z2，若它们实部相等，虚部互为相反数，则称 z1,z2z1,z2 互为 共轭复数。z2z2 是 z1z1 的共轭，z1z1 是 z2z2 的共轭。
• 表示：复数 zz 的共轭记作 z¯¯¯z¯ 或 conj(z)conj⁡(z)。
• 运算性质：两个共轭复数的辐角互为相反数，即 argz1=−argz2arg⁡z1=−arg⁡z2。根据棣莫弗定理，可知 复数积的共轭，等于它们共轭的积。这样理解：求共轭相当于把整个复平面沿 xx 轴翻转，求积再翻转等价于翻转再求积。
• 易知复数和的共轭等于它们共轭的和，且一个复数的共轭的共轭等于它本身。

首先，v(ωkn)=∑n−1i=0vi(ωkn)iv(ωnk)=∑i=0n−1vi(ωnk)i。为了让它和 uu 产生联系，因为 f,gf,g 为实系数多项式，所以 uu 和 vv 的各项系数互为共轭，我们对整个结果求两次共轭，并将一次共轭根据共轭的性质下放至 vivi 和 ωknωnk。

求得 v^v^ 之后，因为 u^=f^+ig^u^=f^+ig^，v^=f^−ig^v^=f^−ig^，所以 f^=u^+v^2f^=u^+v^2，g^=u^−v^2i=(v^−u^)i2g^=u^−v^2i=(v^−u^)i2。

5.1.3 合并两次实系数 IDFT

这里实系数指 IDFT 后的各项系数为实数。如果是 IDFT 前的各项系数为实数，直接使用上一小节的技巧即可。

设需要 IDFT 的两个多项式为 f^f^ 和 g^g^。计算 IDFT(f^)IDFT⁡(f^)，各项系数均为实数，虚部信息被浪费了。考虑计算 IDFT(f^+ig^)IDFT⁡(f^+ig^)，则各项系数的实部即 ff 的系数，虚部即 gg 的系数。

5.2 任意模数卷积

给定两多项式 f,gf,g，在系数模 pp 意义下求出它们的卷积 h=f∗gh=f∗g。

若 pp 不是 NTT 模数，我们不能朴素地使用 FFT 求解该问题，因为 hh 的系数可达 np2np2。取 n=106n=106，p=109p=109，则 np2=1024np2=1024，long double 也无法接受。

接下来介绍两种常见的解决该问题的方法。它们也被称为 MTT（非正式），得名于毛啸 2016 年的集训队论文。

5.2.1 拆系数 FFT

设 B=p–√B=p，将所有系数表示为 kB+r(0≤r<B)kB+r(0≤r<B) 的形式，得到四个多项式 f=f0B+f1f=f0B+f1，g=g0B+g1g=g0B+g1，计算它们两两相乘的结果，则 fg=(f0g0)B2+(f0g1+f1g0)B+f1g1fg=(f0g0)B2+(f0g1+f1g0)B+f1g1。

显然有一个四次 DFT 和三次 IDFT 的朴素做法：对 f0,f1,g0,g1f0,f1,g0,g1 进行 DFT，f^0⋅g^0,f^0⋅g^1+f^1⋅g^0,f^1⋅g^1f^0⋅g^0,f^0⋅g^1+f^1⋅g^0,f^1⋅g^1 进行 IDFT。

使用 6.1.2 和 6.1.3 的技巧，可以做到两次 DFT 和两次 IDFT。系数值域 nB2=np=1015nB2=np=1015，勉强可以接受。

模板题 P4245 任意模数多项式乘法 的 代码。注意用 long double，double 会被卡精度，或者换一种精度较高的 FFT 写法。

5.2.2 三模数 NTT

前置知识：（扩展）中国剩余定理。

选取三个常用 NTT 模数，分别算出 f∗gf∗g 在这些模数下的结果，再使用中国剩余定理合并即可。

我们选择 p1=998244353p1=998244353，p2=1004535809p2=1004535809 和 p3=469762049p3=469762049，设结果分别为 h1,h2,h3h1,h2,h3。

如果使用 CRT，则需要 __int128，因为 hh 的真实值为

使用 exCET 就不需要 __int128：

• 合并 h≡h1(modp1)h≡h1(modp1) 和 h≡h2(modp2)h≡h2(modp2)。设 h=h1+yp1h=h1+yp1，则 h1+yp1≡h2(modp2)h1+yp1≡h2(modp2)，解得 y∈[0,p2)y∈[0,p2) 之后得到 h≡h1+yp1(modp1p2)h≡h1+yp1(modp1p2)，记作 h≡x(modp1p2)h≡x(modp1p2)。
• 合并 h≡x(modp1p2)h≡x(modp1p2) 和 h≡h3(modp3)h≡h3(modp3)。设 h=x+yp1p2h=x+yp1p2，类似解得 y∈[0,p3)y∈[0,p3)，得到 h≡x+yp1p2(modp1p2p3)h≡x+yp1p2(modp1p2p3)。因为 x+yp1p2<p1p2p3x+yp1p2<p1p2p3，所以它就是真实值，可以直接取模。

效率比拆系数 FFT 低不少，因为进行了九次 DFT。代码。

5.3 分治 NTT

前置知识：CDQ 分治。

分治 NTT 在信息竞赛界应用广泛，这归功于他所解决的问题：形如 fi=∑i−1j=0fjgi−jfi=∑j=0i−1fjgi−j 的 半在线卷积。

5.3.1 算法介绍

形如给定 g1∼gn−1g1∼gn−1 和 f0f0，求 f1∼fn−1f1∼fn−1 满足 fi=∑i−1j=0fjgi−jfi=∑j=0i−1fjgi−j 的问题被称为 半在线卷积。因为 fifi 很大，一般会对 NTT 模数 pp 取模。

我们不能通过简单的 NTT 解决这个问题，因为 ff 的每一项均和之前项有关，这要求我们在尝试计算 fifi 时必须已经求出 f0∼fi−1f0∼fi−1，而 NTT 做不到这一点。或者说，它们解决的问题形式不同。

这是一个在线的问题，考虑使用 CDQ 分治 转化为静态问题。

• 设当前分治区间为 [l,r][l,r]，其中 f0∼fl−1f0∼fl−1 对 fl∼frfl∼fr 的贡献已经计算完毕。
• 若 l=rl=r，说明已经求出 flfl，返回。
• 否则，令 m=⌊l+r2⌋m=⌊l+r2⌋，先向左递归 [l,m][l,m] 求解 fl∼fmfl∼fm。
• 为了求解 fm+1∼frfm+1∼fr，我们需要计算 fl∼fmfl∼fm 对它们的贡献：fi=∑mj=lfjgi−jfi=∑j=lmfjgi−j。因为 fl∼fmfl∼fm 已知，所以总的贡献相当于两个已知的多项式相乘的结果。具体地，令 f′j=fj+l(0≤j≤m−l)fj′=fj+l(0≤j≤m−l)，计算 h=f′∗gh=f′∗g，则 fifi 受到 hi−lhi−l 的贡献。
• 向右递归 [m+1,r][m+1,r] 求解 fm+1∼frfm+1∼fr。

因为 f,gf,g 的长度均不超过区间长度，所以时间复杂度 O(nlog2n)O(nlog2⁡n)。

模板题 P4721 分治 FFT 代码：

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
using ull = unsigned long long;

constexpr int N = 1 << 17;
constexpr int mod = 998244353;
void add(int &x, int y) {x += y, x >= mod && (x -= mod);}
int ksm(int a, int b) {
  int s = 1;
  while(b) {
    if(b & 1) s = 1ll * s * a % mod;
    a = 1ll * a * a % mod, b >>= 1;
  }
  return s;
}

int n, f[N], g[N];
void solve(int l, int r) {
  if(l == r) return;
  int m = l + r >> 1, L = 1;
  solve(l, m);
  while(L < r - l + 1) L <<= 1;
  static int a[N], b[N], c[N];
  memset(a, 0, L << 2);
  memcpy(a, f + l, m - l + 1 << 2);
  memcpy(b, g, L << 2);
  NTT(L, a, 1), NTT(L, b, 1);
  for(int i = 0; i < L; i++) c[i] = 1ll * a[i] * b[i] % mod;
  NTT(L, c, 0);
  for(int i = m + 1; i <= r; i++) add(f[i], c[i - l]);
  solve(m + 1, r);
}

int main() {
  cin >> n;
  for(int i = 1; i < n; i++) scanf("%d", &g[i]);
  f[0] = 1, solve(0, n - 1);
  for(int i = 0; i < n; i++) printf("%d%c", f[i], i + 1 < n ? ' ' : '\n');
  return 0;
}

5.3.2 阶梯网格路径计数

阶梯网格路径计数是一类可以使用分治 NTT 解决的经典问题。

给定 n+1n+1 列 m+1m+1 行的网格图，左下角和右上角分别记为 (0,0)(0,0) 和 (n,m)(n,m)。从 (0,0)(0,0) 出发，每次只能向右或向上走，求走到 (n,m)(n,m) 的方案数。让我们回忆：方案数为 (n+mn)(n+mn)。

当然，问题没有这么简单。我们限制第 ii 列不能走到行数大于 cici 的点，其中 cici 单调不降，且 cn=mcn=m。换言之，求出在一个阶梯网格从左下角走到右上角的方案数。

显然有 O(nm)O(nm) 的动态规划：设 fi,jfi,j 表示走到 (i,j)(i,j) 的方案数，则 fi,jfi,j 转移至 fi+1,jfi+1,j 和 fi,j+1fi,j+1。

考虑一段 cici 相同的极长区间 [l,r](l<r)[l,r](l<r) 从 fl,j1fl,j1 转移到 fr,j2fr,j2 的贡献系数：为防止重复计数，从 (l,j1)(l,j1) 出发的第一步应当向右，因此有系数 ((r−l−1)+(j2−j1)r−l−1)((r−l−1)+(j2−j1)r−l−1)。设 gigi 表示 (r−l−1+ii)(r−l−1+ii)，则 fl,j1gi→fr,j1+ifl,j1gi→fr,j1+i，为卷积形式。

在不受 cici 影响的时候，我们确实可以这样做。但是对于每个 ii，它内层的所有 jj 之间也有转移，这让我们不方便借助分治和卷积加快整个过程。考虑进行一些等价转换便于分层。

稍作思考，设 fk,jfk,j 表示走到 (i,j)(i,j) 其中 i+j=ki+j=k 的方案数，则 fk,jfk,j 转移至 fk+1,jfk+1,j 和 fk+1,j+1fk+1,j+1。

进一步地，为了避免在 k>nk>n 时受到 j≥k−nj≥k−n 的限制，考虑从 (n,0)(n,0) 开始沿左上方向把整个阶梯网格劈成两半，分别计算从 (0,0)(0,0) 和 (n,m)(n,m) 到斜对角线上的点（i+j=ni+j=n）的方案数，而这两个问题是对称的。

综合上述分析，我们将问题转化为：从 (0,0)(0,0) 出发，每次可以向右或右上走一步，求走到最右侧一列每个点的方案数。其中，在第 ii 列不能走到行数大于 cici 的点。这个 cici 可通过原问题的 cici 进行简单转化得到，且容易证明其仍不降且满足很好的性质：ci+1−ci≤1ci+1−ci≤1。

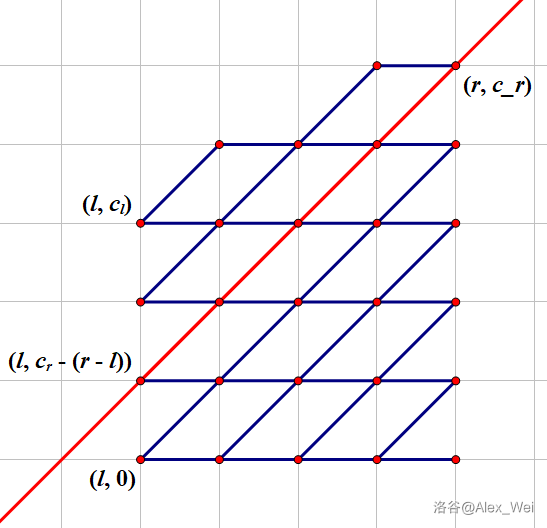
因此，从 flfl 推到 frfr 的时候，我们会发现对于 j≤cr−(r−l)j≤cr−(r−l)，设不等号右侧的数为 xx，fl,jfl,j 对 frfr 的贡献不会受到 cc 的影响：因为 ci+1−ci≤1ci+1−ci≤1，所以从 (l,j)(l,j) 开始，就算每一步都往右上走，也不会突破限制。这样，fl,0∼fl,xfl,0∼fl,x 对 frfr 的贡献可直接卷积计算。对于 fl,x+1∼fl,clfl,x+1∼fl,cl，分治下放至左右子区间 (l,m](l,m] 和 (m,r](m,r] 进行递归。

有了大致思路，设计算法就很简单了：设 solve(l,r,Δ,F)solve(l,r,Δ,F) 表示当前区间为 (l,r](l,r]，传入多项式 FF 的第 ii 项表示 fl,i+Δfl,i+Δ，返回多项式 GG 的第 ii 项表示 fr,i+Δfr,i+Δ。也可视作暂时将 cl∼crcl∼cr 全部减去 ΔΔ，传入 fl=Ffl=F，返回 G=frG=fr，接下来就使用这种视角。

对于 j≤cr−(r−l)j≤cr−(r−l)，设不等号右侧的数为 xx，F0∼FxF0∼Fx 和 H0∼Hr−lH0∼Hr−l 卷积求出 F0∼FxF0∼Fx 转移得到的 G0∼GcrG0∼Gcr，其中 HiHi 即转移系数 (r−li)(r−li)。

对于 j>xj>x，分治下放：设 F′=Fx+1∼FclF′=Fx+1∼Fcl，mid=⌊l+r2⌋mid=⌊l+r2⌋，则先递归左半部分 F′←solve(l,mid,Δ+x+1,F′)F′←solve(l,mid,Δ+x+1,F′)，再递归右半部分 F′←solve(mid,r,Δ+x+1,F′)F′←solve(mid,r,Δ+x+1,F′)，则此时 F′F′ 表示从 Fx+1∼FclFx+1∼Fcl 转移得到的 Gx+1∼GcrGx+1∼Gcr。

两部分相加即得 GG，返回即可。

边界 r−l=1r−l=1 的处理是平凡的。

两次下传 F′F′ 时，F′F′ 的长度显然不超过 cr−x=r−lcr−x=r−l，因此在处理区间 (l,r](l,r] 时涉及到的所有多项式的长度均不超过其父区间长度。设 n,mn,m 同级，则时间复杂度为 O(nlog2n)O(nlog2⁡n)。

接下来对问题进行一些扩展：

• 如果没有 ci+1−ci≤1ci+1−ci≤1 的性质，但 cici 单调不降，还能做吗？答案是可以，只需将 xx 的定义改为 cl−(r−l)cl−(r−l)，此时 (l,r](l,r] 涉及到的多项式长度不超过父区间的长度加上端点处 cc 的差值，可以接受。

5.4 例题

CF1770G Koxia and Bracket

相比于 F，这道题就略显套路了。

将左括号视为 11，右括号视为 −1−1，找到最后一个使得前缀和小于 00 的位置 lstlst，则 s1∼slsts1∼slst 的每个左括号都有用，必然不会删去。同理，slst+1∼snslst+1∼sn 的每个右括号也都有用。

对于 s1∼slsts1∼slst 的每个右括号 sisi，如果它对应的前缀和为 cici，则为保证前缀和非负，在 s1∼sis1∼si 中至少需要删掉 −ci−ci 个右括号。我们只关心 −ci−ci 的前缀最大值，因为若这些位置满足条件，则所有位置满足条件，而每个前缀最大值一定会比先前的前缀最大值大 11，所以我们将问题转化为：给定长为 mm 的序列，其中有 cc 个位置被打上了标记，求出选择 cc 个位置的方案数，使得对于每个前缀，选择的位置数不小于被打上标记的位置数。

设 fi,jfi,j 表示考虑到第 ii 个位置，当前选择位置数减去打标记位置数的数量为 jj。对于没有被打标记的位置 pp，fp−1,jfp−1,j 转移到 fp,j/j+1fp,j/j+1，否则转移到 fp,j−1/jfp,j−1/j。

非常明显的阶梯格路计数问题，稍有变形，不过解法大差不差，核心思想是一致的：考虑 flfl 转移到 frfr，用卷积描述一部分转移，剩下来 O(r−l)O(r−l) 个位置分别递归两侧处理。

对于本题，就是 fl,j(j≥cnt)fl,j(j≥cnt) 对 frfr 的贡献用卷积描述，其中 cntcnt 表示 l+1∼rl+1∼r 的被打上标记的位置。剩余部分递归，长度只有 cntcnt，而且因为截取的是低位，我们甚至不需要记录偏移量 ΔΔ。

r−l=1r−l=1 的边界情况是平凡的。

slst+1∼snslst+1∼sn 的左括号类似处理即可。

每个分治区间涉及到的多项式长度不超过其父区间长度，因此时间复杂度为 O(nlog2n)O(nlog2⁡n)。代码。

• P3803 题解 - NaCly_Fish。
• 2016 集训队论文《再探快速傅里叶变换》—— 毛啸。

__EOF__