贪心算法Dijkstra - Galaxy不写bug

Dijkstra#

最短路径问题 : 给定一个带权有向图 G = (V, E, W)，同时给定一个源点 u (u ∈ V)，我们要找出从源点 u 出发到其它各点的最短路径距离，并得出这些最短路径的具体路径有哪些边构成。

其实我们要求的就是从 源点 u 出发到 其它各点 str的最短路径所组成的路线网络，也就是一个 最短路径树。

最短路径问题 : 给定一个带权有向图 G = (V, E, W)，同时给定一个源点 u (u ∈ V)，我们要找出从源点 u 出发到其它各点的最短路径距离，并得出这些最短路径的具体路径有哪些边构成。

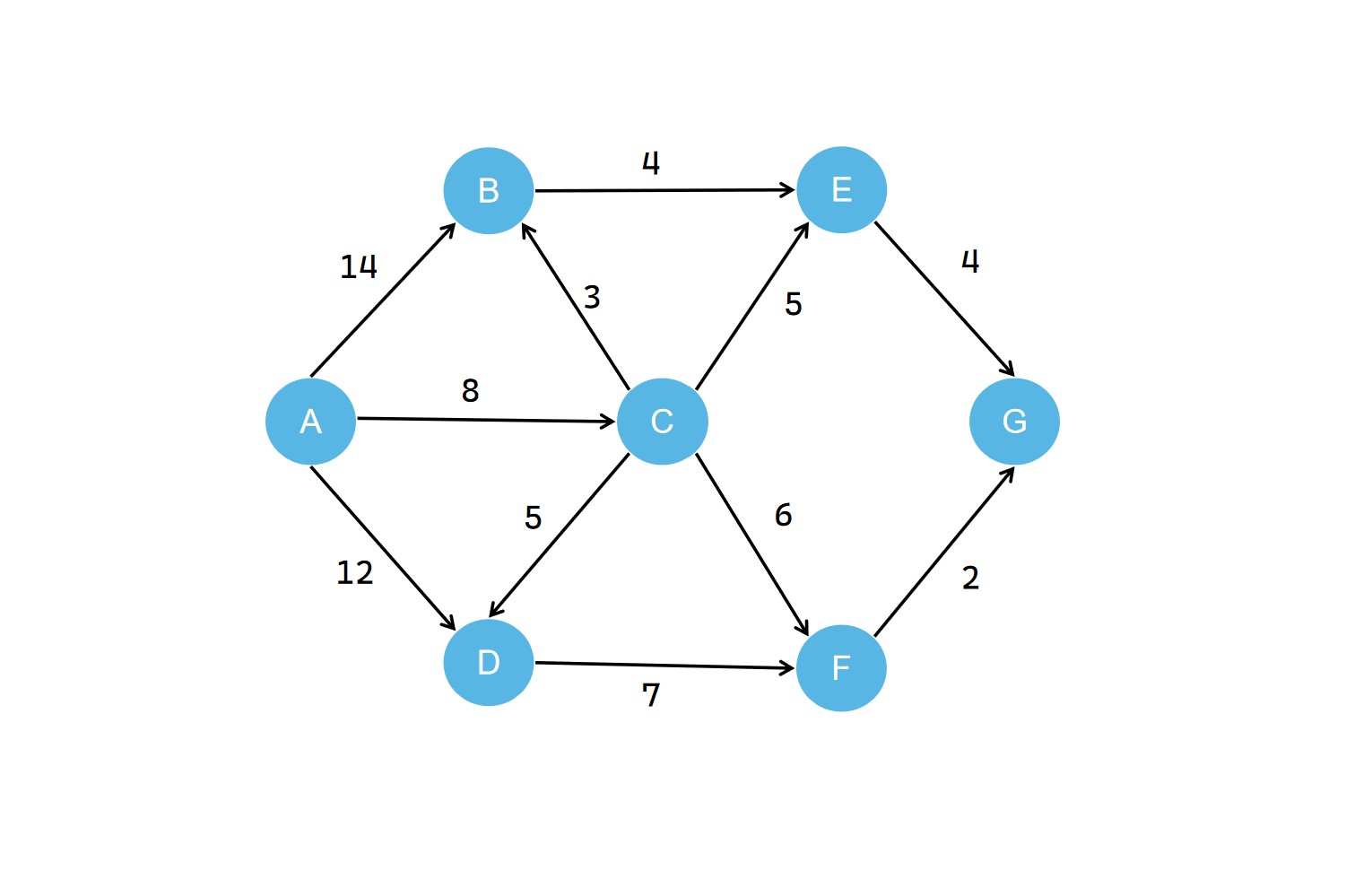
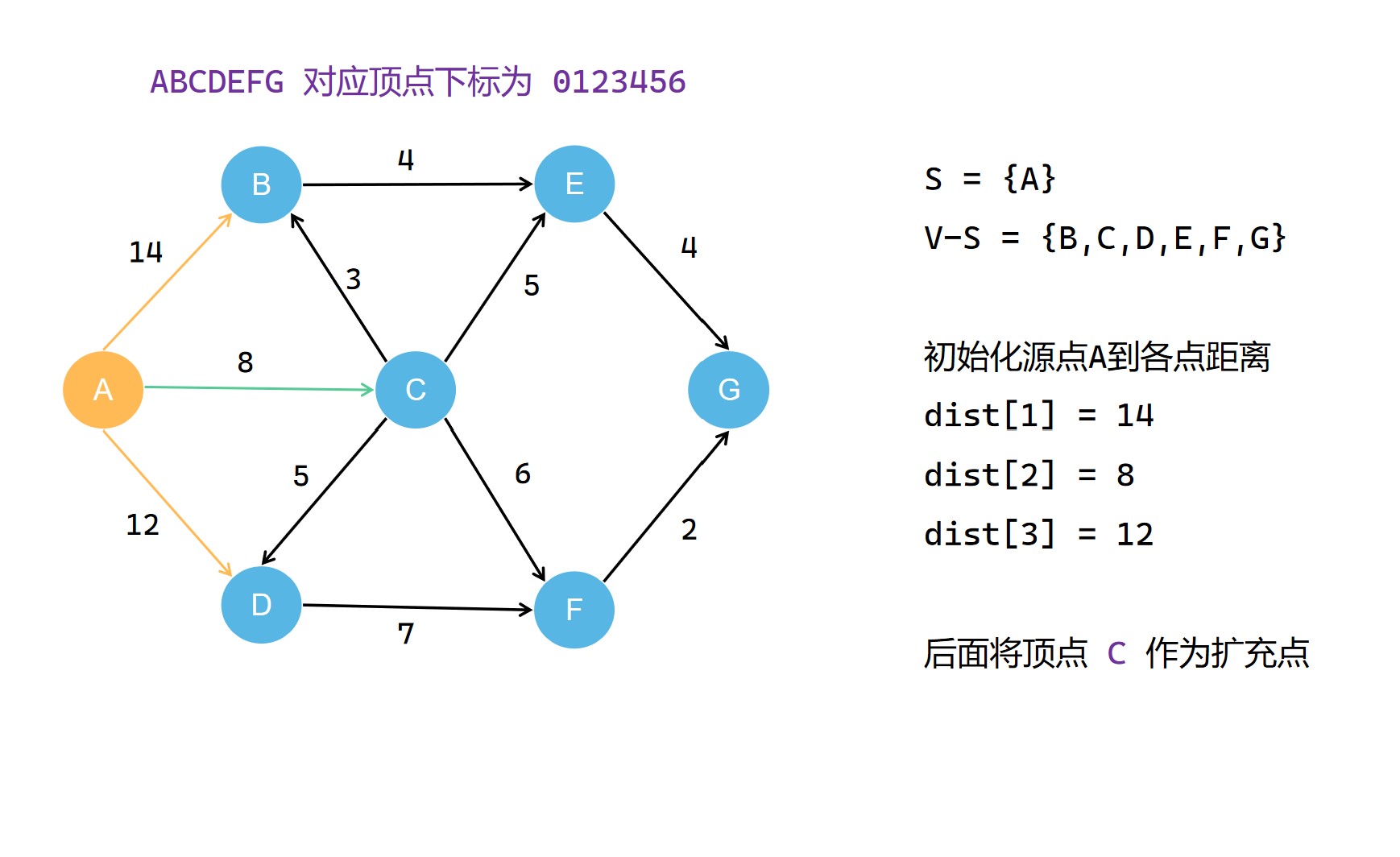
我们以下面这个带权有向图为示例

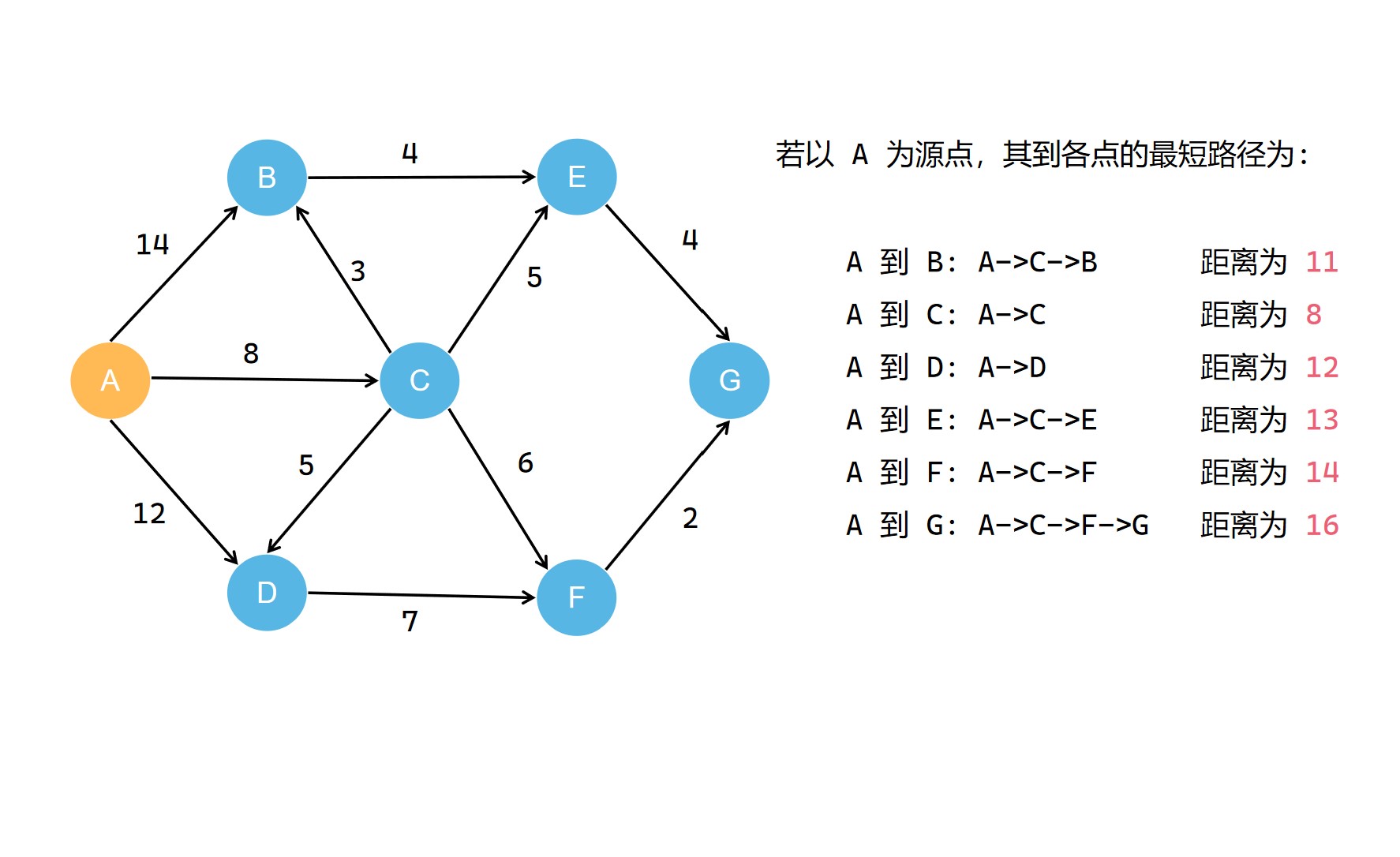
我们若以 A 为源点，得到如下的最短路径

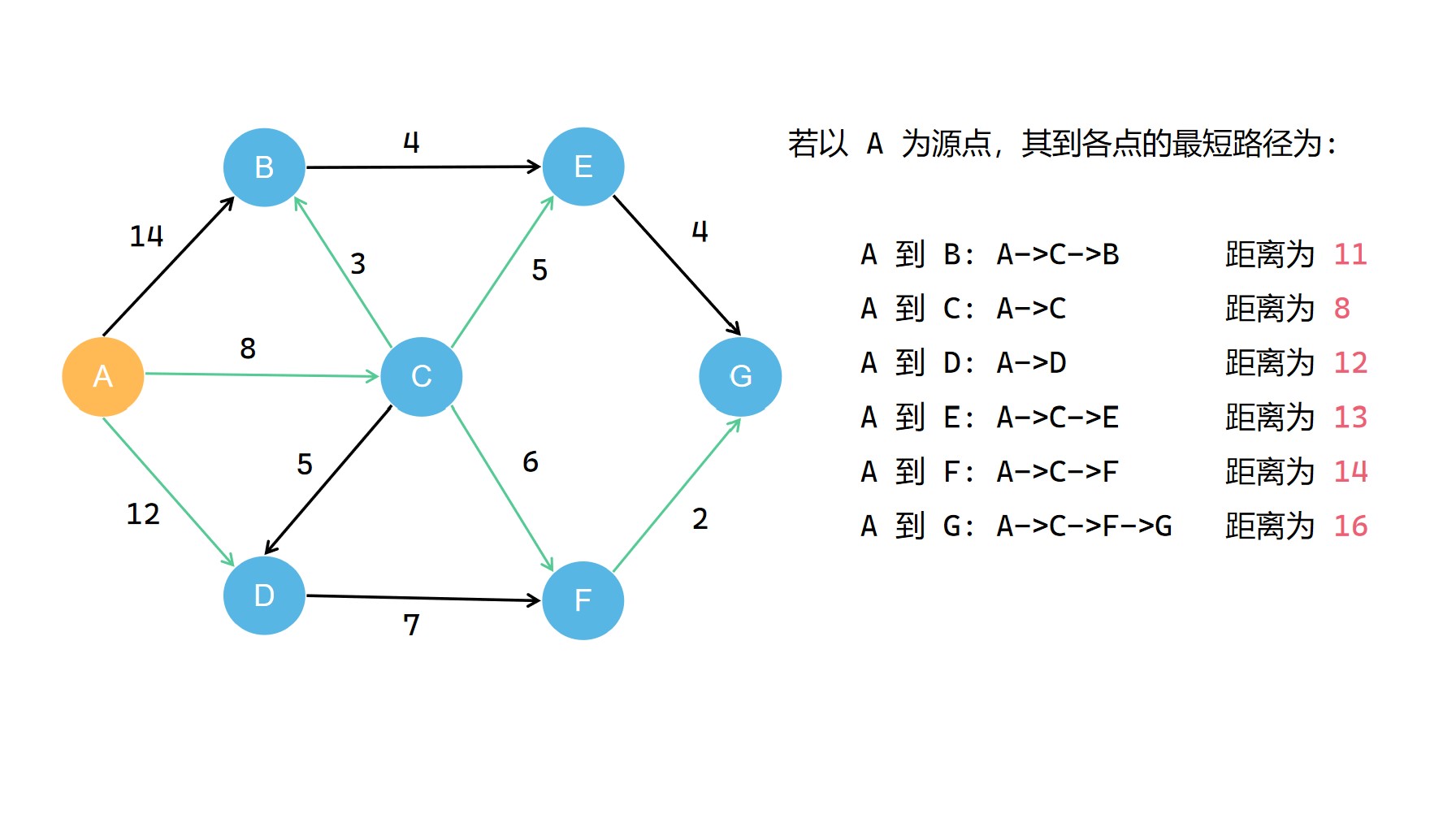
我们可以把源点到各点最短路径用绿色标记一下

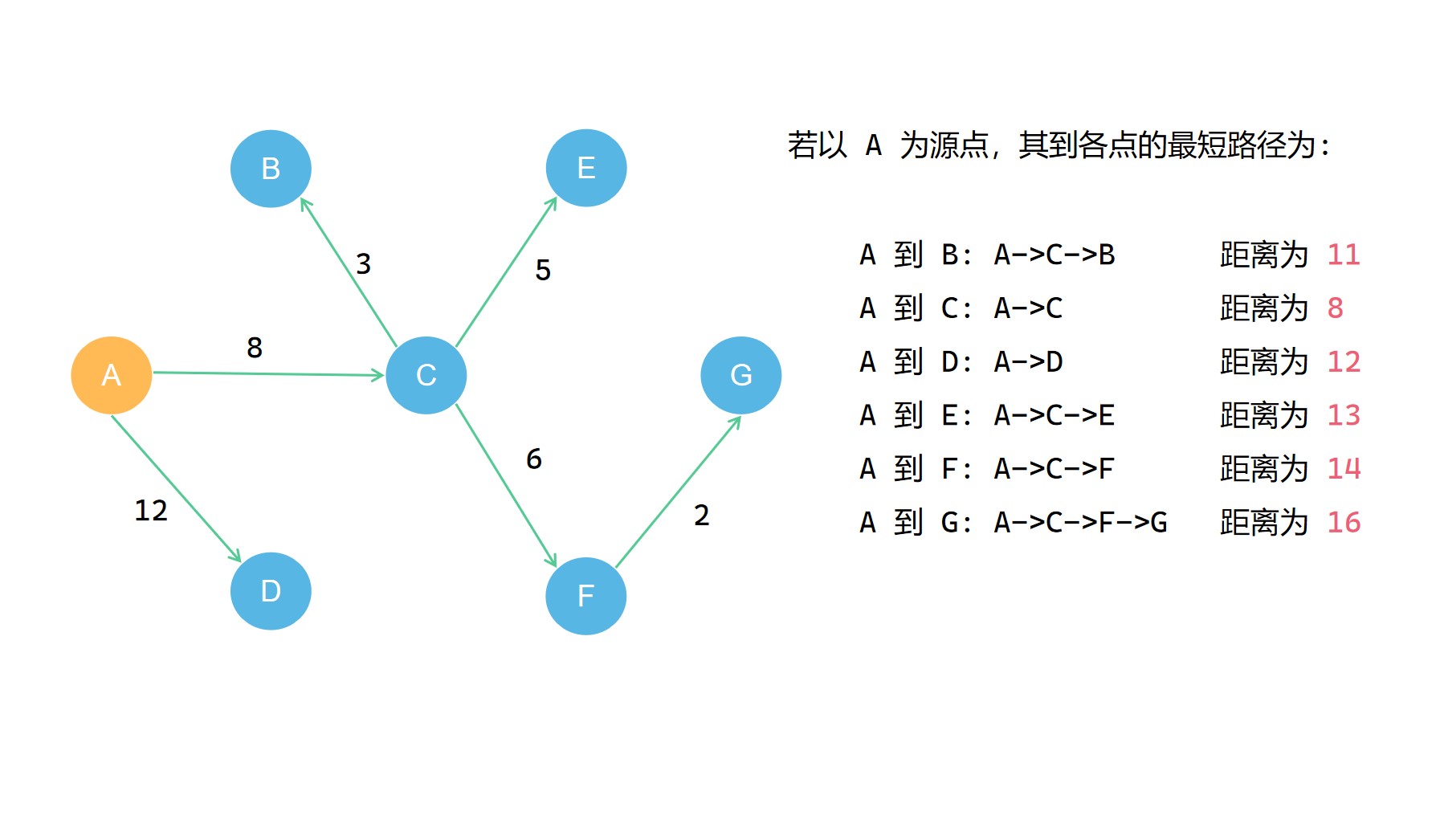
我们可以看出所有的最短路径构成了一个最短路径树

我们要求的从 源点 到 其它各点 的最短路径所组成的路线网络，就是这个最短路径树。

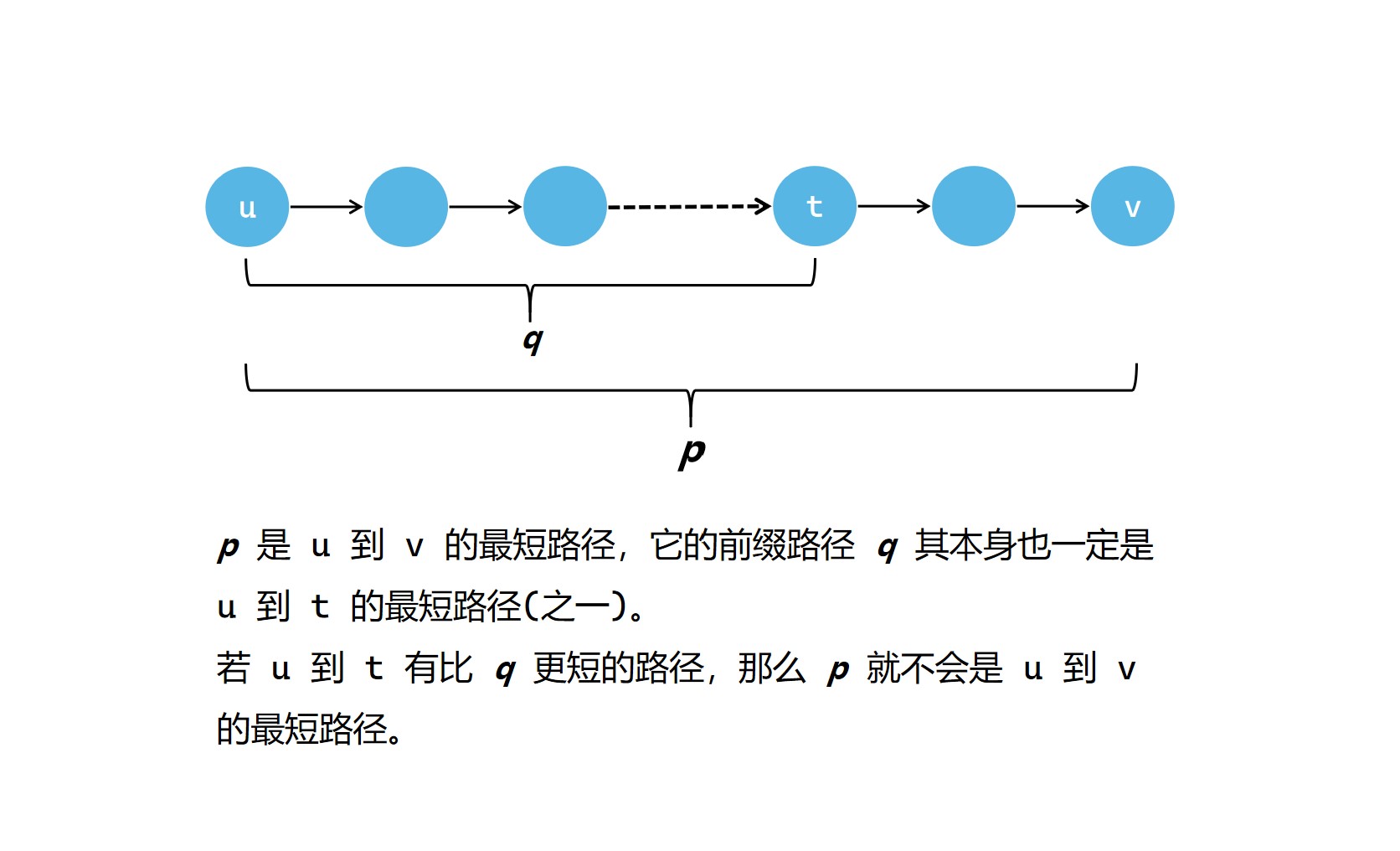
在上面的图中，我们不难发现，当我们确定了源点 u 到某个其它的点 v 的最短路径时，在这个最短路径的具体路线中，若有一个中转点 t，那么在这个最短路径中从源点 u 到 t 的路径也一定是 u 到 t 的最短路径(之一)。也就是说，假设源点 u 到 v 的最短路径为 p，那么p任意的前缀路径 q 一定是最优的(最短路径之一)。如果 q 不是最优的，那么就会存在另一个更短的路径比 p 更短。

这个性质还是很重要的，是解决单源最短路径问题的核心

我们画个图来理解一下

歧义性

在上面的阐述中也稍微提到一点，就是最短路径其实不一定是唯一的，有可能存在两个路径，它们的路径距离一样且都是最短的，那么此时我们二选其一就可以啦。还有一个问题就是，我们的边权都应当是正数，如果边权存在非正数，那么我们是无法定义这个图中的最短路径的(距离确实不能是非正数呀，除了自己到自己🤔)。

无环性

这个性质其实很好理解，既然我们得到的所有最短路径构成的是一个 最短路径树，那么作为一个树，它必不会存在环。也可以由之前的 单调性 得出这个性质。

---

Dijkstra 算法是由荷兰计算机科学家 Edsger Wybe Dijkstra 在1956年提出的，一般解决的是 带权有向图 的 单源最短路径问题。
接下来介绍如何用 Dijkstra 算法求解 单源最短路径问题。

Dijkstra 算法将会充分利用 最短路径树 的 单调性 这一性质。先定下源点 u，然后采用 贪心 的策略，不断去访问与源点 u 相接且之前未被访问过的最近的顶点 v(这句话里相接的意思是指可以从 u 到达 v)，使得当前的最短路径树得到扩充，一直到所有顶点都在当前的最短路径树中，那么就得到了源点 u 到其他所有顶点 v 的最短路径。

我们将当前最短路径树所有的顶点所构成的集合称为 集合S，而不在当前最短路径树中的顶点所构成的集合称为集合V-S。

1、首先需要定义一个辅助数组 flag[]，用于标记每个顶点是否处于当前的 最短路径树 中，后续我们将 最短路径树 称为 集合S。在初始情况下，我们会先将源点 u 划入 集合S;

2、然后我们需要再定义一个数组 dist[]，用于记录当前从源点 u 到 v (v∈V-S)的最短路径距离，比如dist[vi]就表示 u 到 vi 的当前最短路径距离。

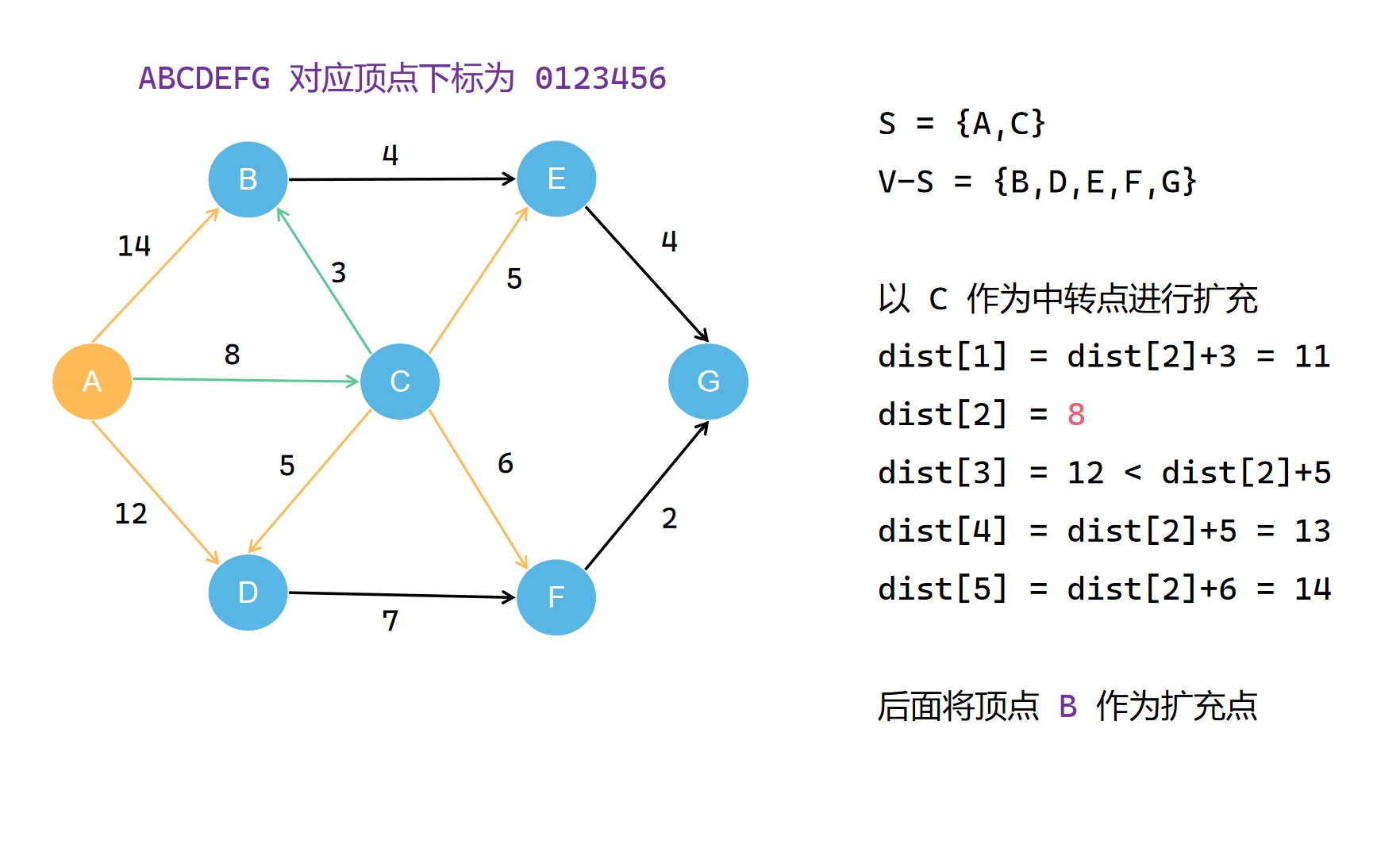
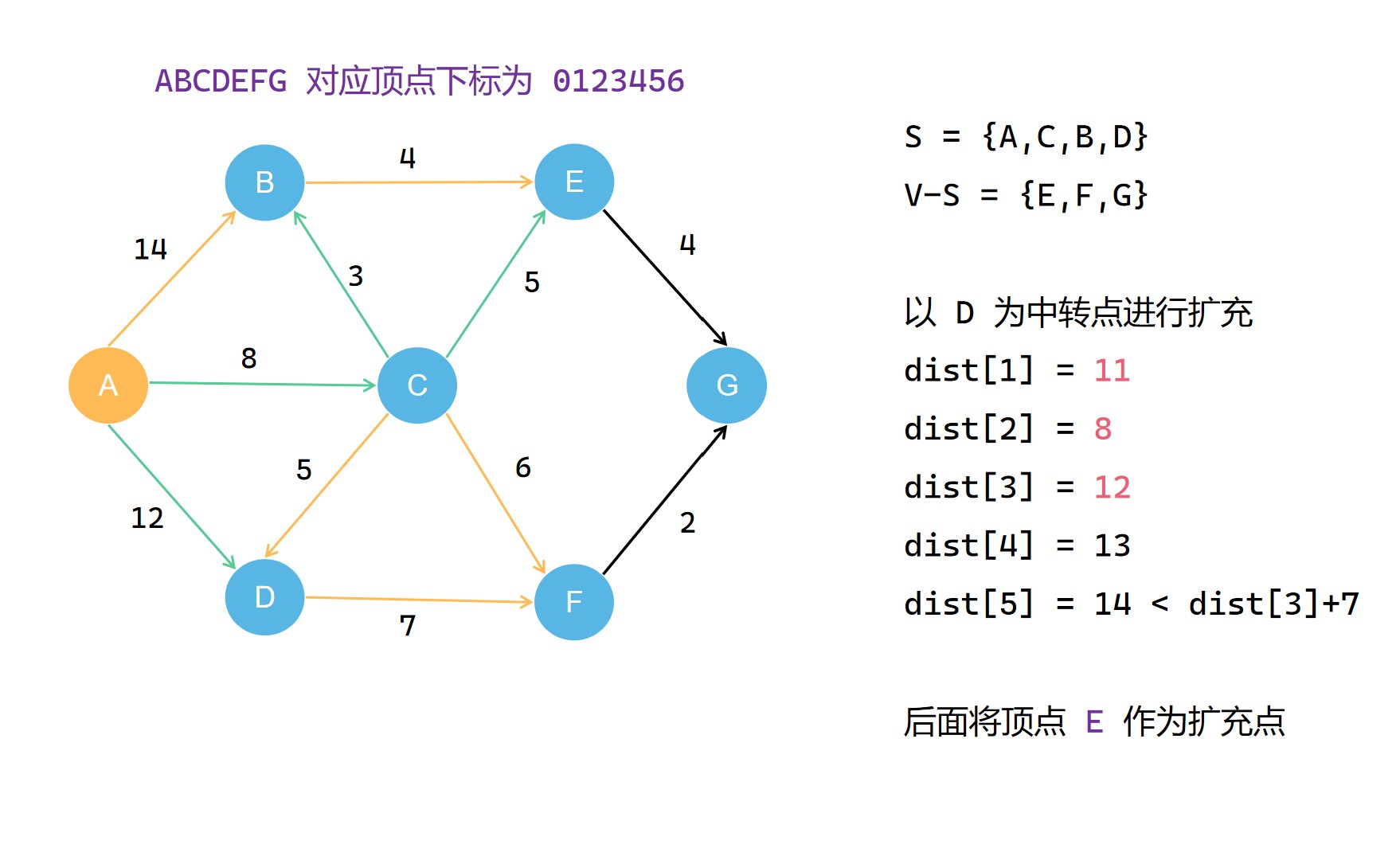
集合S每一次扩充都需要选择当前不在集合S中且到源点 u 最短距离的顶点 t 作为扩充点，并且将其划入集合S。之后的扩充操作中，就以这个 t 作为中转点对 dist[v] 进行更新，使其记录的距离减小。在不断扩充集合S的过程中，dist[v]的记录的距离大小不断减小(可能不变)，直到最后，其记录的便是整个图中u 到 v 的最短的距离；

另外，一开始我们要先初始化源点 u 到其邻接的顶点的距离。

3、为了还原具体路径，我们还需要一个辅助数组 pre[]，用于记录最短路径中每个顶点的前驱顶点。比如 pre[v]，其记录的是 u 到 v 的最短路径中，顶点 v 的前驱顶点。在不断扩充集合S的过程中，如果可以借助当前的扩充点 t 到达 v 的距离更短，我们也要更新 v 的前驱为 t，即 pre[v] = t 。

同样的，我们也要初始化源点 u 为其每个邻接顶点的前驱。

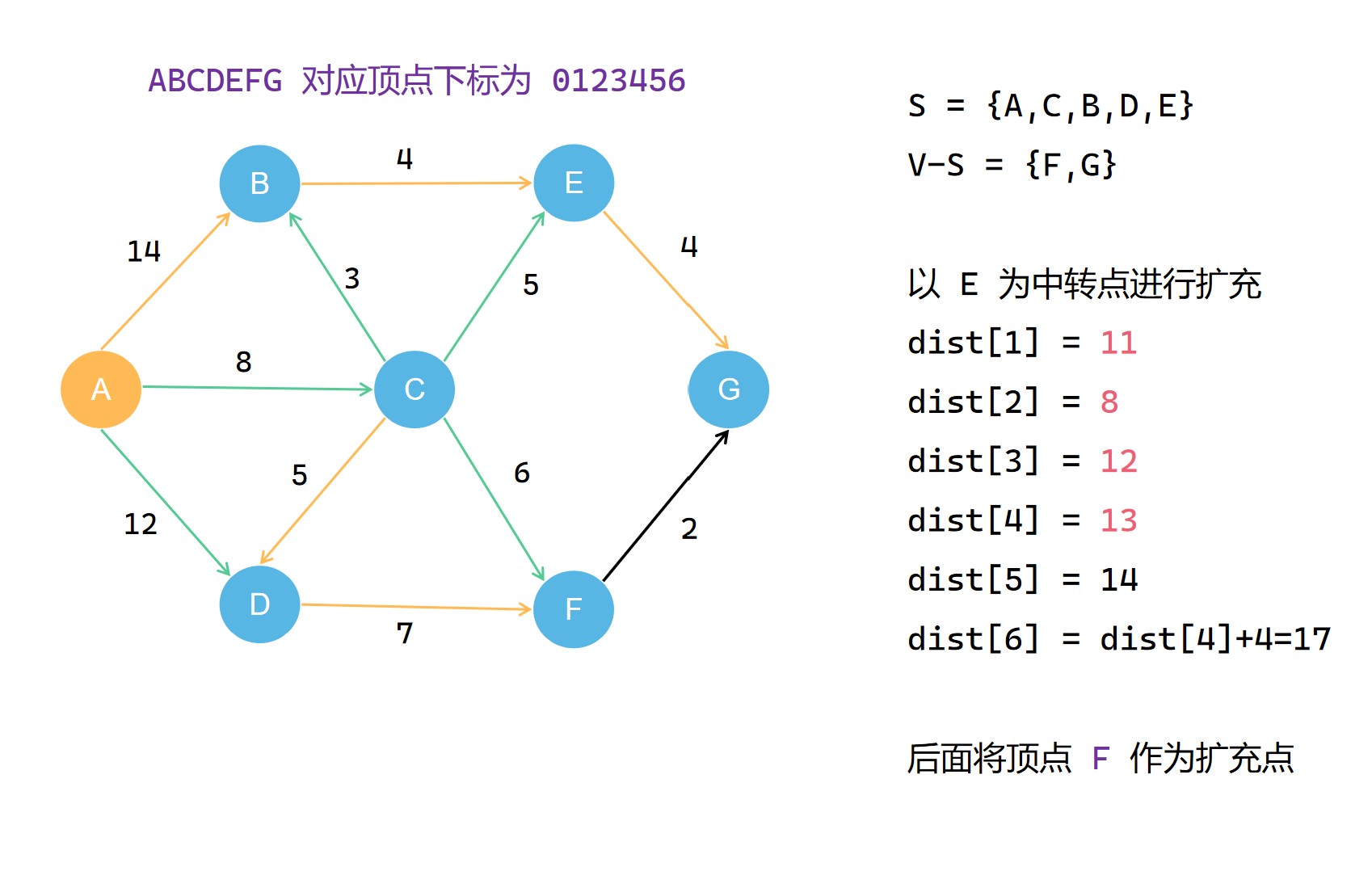
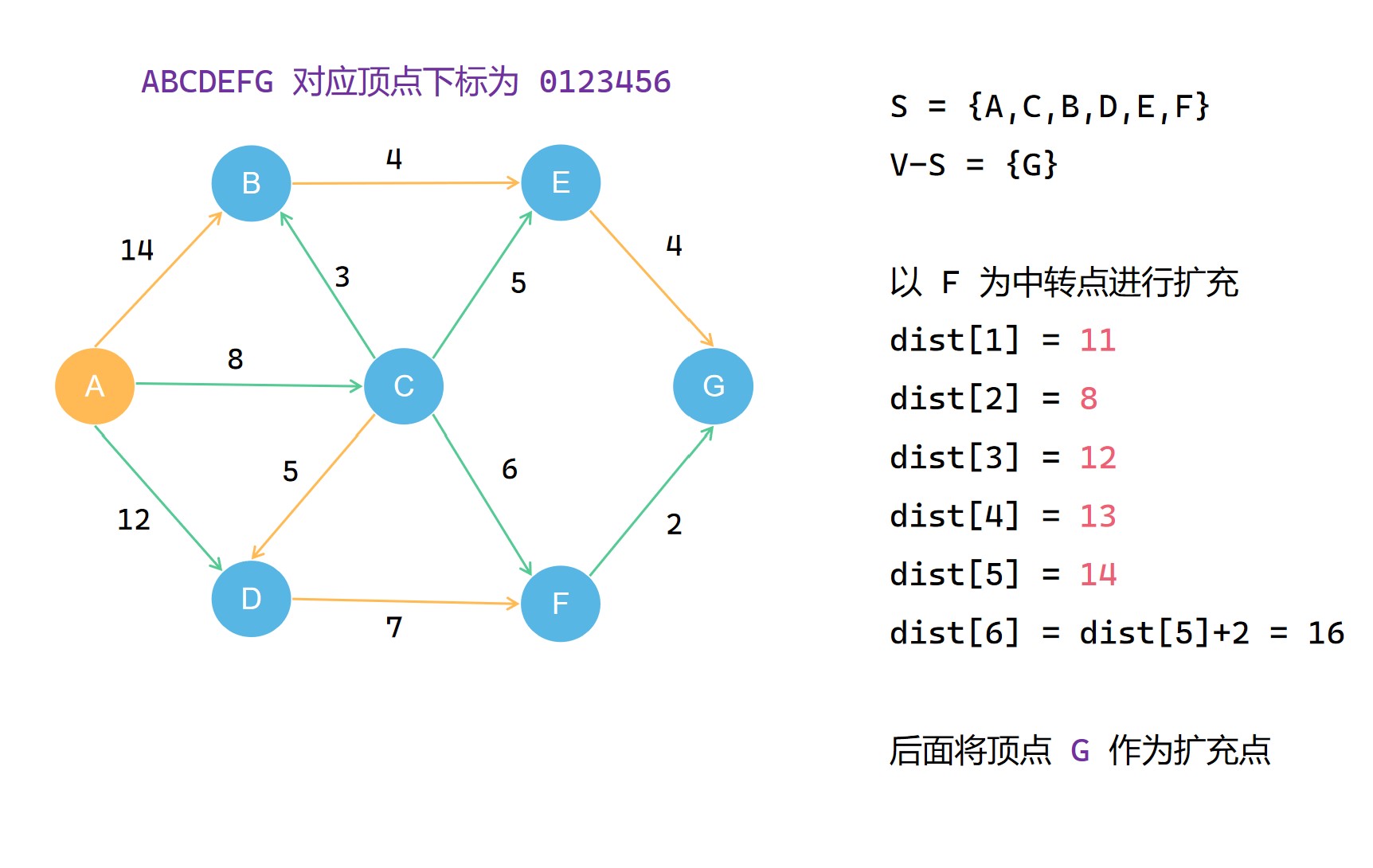
(2)

(3)

(4)

(5)

(6)

(7)

---

以下程序是基于 图的邻接矩阵 实现的

//距离记录数组 , 前驱数组
int dist[MAX], pre[MAX];  
//集合S标记数组。如果flag[i]=true,说明该顶点i已经加入到集合S(最短路径集合);否则i属于集合V-S
bool flag[MAX];            

void Dijkstra(Graph *G, int u){
    for(int v = 0; v < G->nodenums; v++){
        dist[v] = G->edge[u][v];  //初始化源点u到各邻接点v的距离
        flag[v] = false;
        if(dist[v] != INF)
            pre[v] = u;           //若有邻接边,顶点v有前驱顶点u
        else
            pre[v] = -1;          //若没有,先初始化为-1
    }
    flag[u] = true;               //初始化集合S,只有一个元素: 源点u
    dist[u] = 0;                  //初始化源点u到自己的最短路径为0
    
    
    for(int i = 0; i < G->nodenums; i++){
    	int tmp = INF, t = u;
        /*  在集合V-S中寻找距离源点u最近的顶点t,使当前最短路径树最优  */
    	for(int v = 0; v < G->nodenums; v++){
    	    if(!flag[v] && dist[v] < tmp){
                //不在集合S中 并且 更小距离
                t = v;           
                //记录在V-S中距离源点u最近的顶点v
                tmp = dist[v];
    	    }
    	}

    	if(t == u)
    	    return;               //未找到直接终止
    	flag[t] = true;           //否则, 将t加入集合S
        
        /*   更新集合V-S中与t邻接的顶点到u的距离,扩展当前最短路径树  */
    	for(int v = 0; v < G->nodenums; v++){
            //不在集合S中 且 有边
    	    if(!flag[v] && G->edge[t][v] != INF){
                if(dist[v] > dist[t] + G->edge[t][v]){
                    //源点u可以借助t到达v的距离更短
                    dist[v] = dist[t] + G->edge[t][v];
                    pre[v] = t;
                }
    	    }
    	}
    }
}

---

还原具体路径代码

我使用了 C++ 自带的 栈 stack，来实现最短路径具体路径的还原。因为记录的是每个顶点的前驱，所以恰好可以利用 栈 stack 的先进后出的性质。

//还原源点u到各点具体路径
void ShowShortPath(Graph G, int u){
    for(int v = 0; v < G.nodenums; v++){
        if(dist[v] == INF || dist[v] == 0)
            continue;
        cout<<"\n点"<<G.apex[u]<<" 到 点"<<G.apex[v]<<" 的最短路径距离为: "<<dist[v]<<endl;
        cout<<"点"<<G.apex[v]<<"的前驱顶点为: 点"<<G.apex[pre[v]]<<endl;
        cout<<"具体路径为: "<<endl;

        int t = pre[v];           //终点的前驱下标
        //用栈存储终点前驱们 一直到 源点
        stack<int> st;            
        while(t != u){
            st.push(t);
            t = pre[st.top()];
	}

    cout<<G.apex[u];          		//源点
	while(!st.empty()){
	    t = st.top();
	    cout<<" --> "<<G.apex[t];   //中间点
	    st.pop();
        }
	cout<<" --> "<<G.apex[v]<<endl; //终点
	cout<<"———————————————————"<<endl;
    }
}

---

完整程序(含图的邻接矩阵)

#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
const int MAX = 100;
const int INF = 1e7;

typedef char ApexType;			//顶点名称数据类型
typedef int EdgeType;			//边权数据类型

typedef struct {

	ApexType apex[MAX];			//顶点表
	EdgeType edge[MAX][MAX];	//矩阵图
	int nodenums, edgenums;		//顶点个数，边个数

}Graph;

//创建邻接矩阵
void CreateGraph(Graph *G){
    int i, j, k;
    int w;
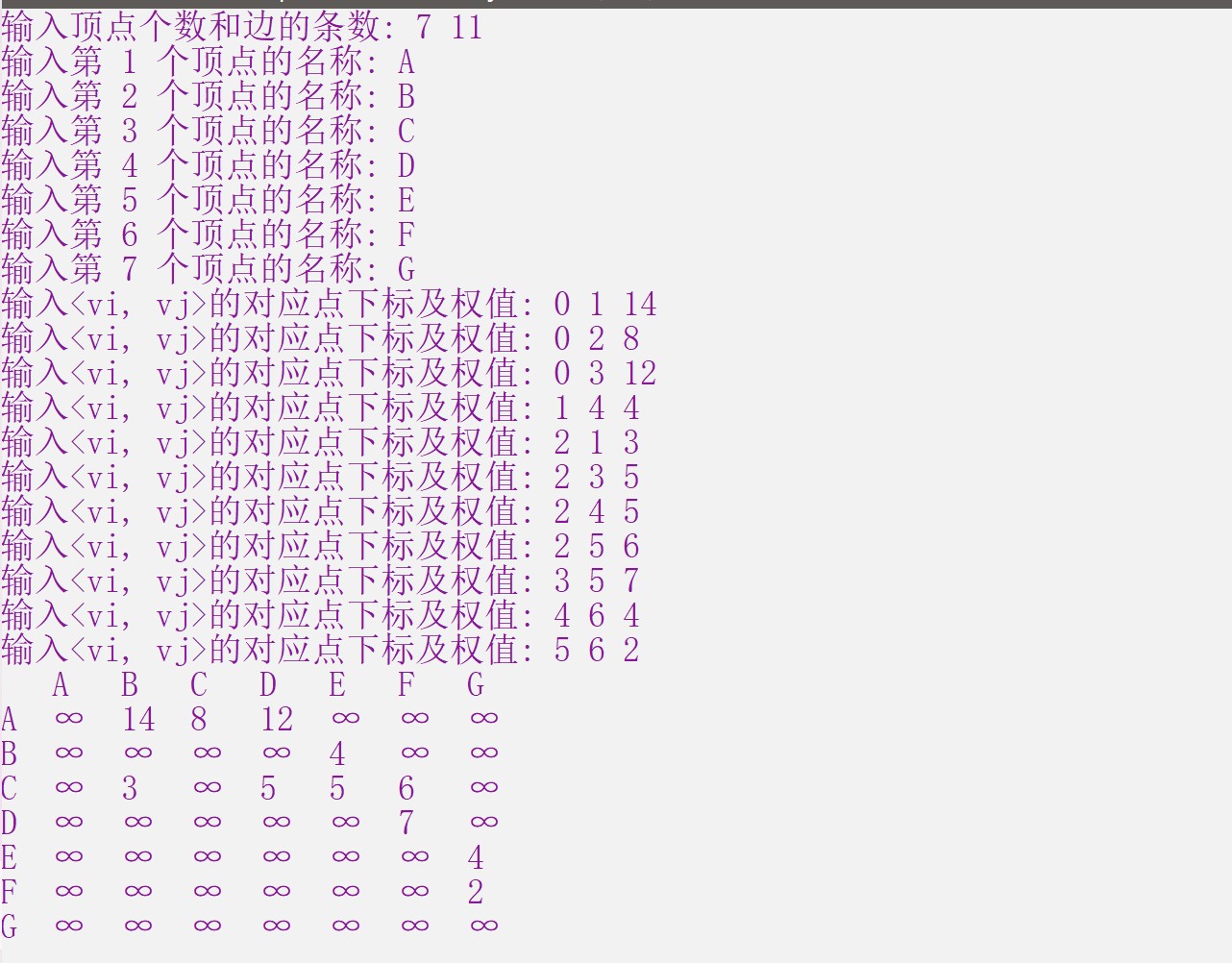
    cout<<"输入顶点个数和边的条数: ";
    cin>>G->nodenums>>G->edgenums;
    //输入顶点信息
    for(i = 0; i < G->nodenums; i++){
	cout<<"输入第 "<<i + 1<<" 个顶点的名称: ";
	cin>>G->apex[i];
    }
    //初始化各顶点之间的边为无穷大
    for(i = 0; i < G->nodenums; i++)
	for(j = 0; j < G->nodenums; j++)
	    G->edge[i][j] = INF;             
    //录入有向边的信息
    for(k = 0; k < G->edgenums; k++){
        EdgeType w;
        cout<<"输入<vi, vj>的对应点下标及权值: ";
        cin>>i>>j>>w;
        G->edge[i][j] = w;
    }
}

//打印图的邻接矩阵
void ShowGraphInMatrix(Graph *G){
    cout<<"   ";
    for(int i = 0; i < G->nodenums; i++)
		printf("%4c",G->apex[i]);
    cout<<endl;

    for(int i = 0; i < G->nodenums; i++){
		printf("%3c", G->apex[i]);
        for(int j = 0; j < G->nodenums; j++){
            if(G->edge[i][j] == INF)
                cout<<"∞  ";
            else
                printf("%4d", G->edge[i][j]);
        }
		cout<<endl;
    }		
}

//距离记录数组 , 前驱数组
int dist[MAX], pre[MAX];  
//集合S标记数组。如果flag[i]=true,说明该顶点i已经加入到集合S(最短路径集合);否则i属于集合V-S
bool flag[MAX];            

void Dijkstra(Graph *G, int u){
    for(int v = 0; v < G->nodenums; v++){
        dist[v] = G->edge[u][v];  //初始化源点u到各邻接点v的距离
        flag[v] = false;
        if(dist[v] != INF)
            pre[v] = u;           //若有邻接边,顶点v有前驱顶点u
        else
            pre[v] = -1;          //若没有,先初始化为-1
    }
    flag[u] = true;               //初始化集合S,只有一个元素: 源点u
    dist[u] = 0;                  //初始化源点u到自己的最短路径为0
    
    /*   在集合V-S中寻找距离源点u最近的顶点t,使当前最短路径树最优  */
    for(int i = 0; i < G->nodenums; i++){
    	int tmp = INF, t = u;
    	for(int v = 0; v < G->nodenums; v++){
    	    if(!flag[v] && dist[v] < tmp){
                //不在集合S中 并且 更小距离
                t = v;            
                //记录在V-S中距离源点u最近的顶点v
                tmp = dist[v];
    	    }
    	}

    	if(t == u)
    	    return;               //未找到直接终止
    	flag[t] = true;           //否则, 将t加入集合S
        
        /*   更新集合V-S中与t邻接的顶点到u的距离,扩展当前最短路径树  */
    	for(int v = 0; v < G->nodenums; v++){
    	    if(!flag[v] && G->edge[t][v] != INF){
    		//不在集合S中 且 有边
                if(dist[v] > dist[t] + G->edge[t][v]){
                    //源点u可以借助t到达v的距离更短
                    dist[v] = dist[t] + G->edge[t][v];
                    pre[v] = t;
                }
    	    }
    	}
    }
}

//还原源点u到各点具体路径
void ShowShortParth(Graph G, int u){
    for(int v = 0; v < G.nodenums; v++){
	if(dist[v] == INF || dist[v] == 0)
	    continue;
	cout<<"\n点"<<G.apex[u]<<" 到 点"<<G.apex[v]<<" 的最短路径距离为: "<<dist[v]<<endl;
	cout<<"点"<<G.apex[v]<<"的前驱顶点为: 点"<<G.apex[pre[v]]<<endl;
	cout<<"具体路径为: "<<endl;

	int t = pre[v];           //终点的前驱下标
	//用栈存储终点前驱们 一直到 源点
	stack<int> st;            
	while(t != u){
	    st.push(t);
	    t = pre[st.top()];
	}

    	cout<<G.apex[u];          		//源点
	while(!st.empty()){
	    t = st.top();
	    cout<<" --> "<<G.apex[t];   //中间点
	    st.pop();
        }
	cout<<" --> "<<G.apex[v]<<endl; //终点
	cout<<"———————————————————"<<endl;
    }
}


main(){
    Graph G;
    CreateGraph(&G);
    ShowGraphInMatrix(&G);
    
    int u;
    cout << "\n输入出发的源点下标: ";
    cin>>u;

    Dijkstra(&G, u);
    
    cout<<"\n源点到所有点的单源最短路径距离:"<<endl;
    ShowShortParth(G, v);
}

---

单源最短路径及具体路径

原文链接:[最短路径问题]Dijkstra算法(含还原具体路径) - Amαdeus - 博客园 (cnblogs.com)