

.ai | 神经网络中的卷积及其参数
source link: https://mountaye.github.io/blog/articles/parameters-in-convolution-in-neural-network-and-transposeconv
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

在读 PyTorch 的文档和源码的时候,发现写文档的人也不怎么解释啥是卷积,卷积的各个参数是什么意思,只在文档里扔了个链接就完事了,链接那头是一个 GitHub 上的动图演示仓库,是一篇论文《A guide to convolution arithmetic for deep learning》(链接在文末)的附件。于是这篇文章,基本上就是论文的读书笔记了。
数学的卷积:连续 vs. 离散
连续的情况,两个单变量函数 f(⋅)f(⋅) 和 g(⋅)g(⋅) 的卷积,定义为:
(f∗g)(x):=∫∞−∞f(τ)g(x−τ)dτ(f∗g)(x):=∫−∞∞f(τ)g(x−τ)dτ
离散的情况,两个向量(也就是一阶张量) ⃗ff→ 和 ⃗gg→ 的卷积,定义为:
(⃗f∗⃗g)i:=∞∑j=−∞fjgi−j(f→∗g→)i:=∑j=−∞∞fjgi−j
多变量函数/高阶张量的情况,只需要多加几重积分/求和号就可以类推了。
看这两个定义——
只看等号左边的话,可以把卷积看作是一种特殊的乘法,也就是一种运算。f 和 g 的地位是平等的,卷积甚至还满足交换律,你甚至可以把两者的顺序变一变;
但是看等号右边的话,卷积就应该被看作是一种变换。f 和 g 的地位不再平等,f 是被变换的函数/向量,g 是变换的核 (kernel)。函数的情况里,g 把定义在 ττ 空间里的函数 f 变换成了 x 空间里的另一个函数;向量的情况里,g 把一个 J (j 所有可能取值的数量) 维向量 f 变换成了一个 I (i 所有可能取值的数量) 维向量。
神经网络中的卷积,借用的主要是第二种理解。
手算一个例子
例如 ⃗f=(1,2,3,4)f→=(1,2,3,4), ⃗g=(1,2,3)g→=(1,2,3),而且约定下标从 0 开始的话——
(⃗f∗⃗g)0=f0g0=1(f→∗g→)0=f0g0=1
(⃗f∗⃗g)1=f0g1+f1g0=4(f→∗g→)1=f0g1+f1g0=4
(⃗f∗⃗g)2=f0g2+f1g1+f2g0=10(f→∗g→)2=f0g2+f1g1+f2g0=10
(⃗f∗⃗g)3=f1g2+f2g1+f3g0=16(f→∗g→)3=f1g2+f2g1+f3g0=16
(⃗f∗⃗g)4=f2g2+f3g1=17(f→∗g→)4=f2g2+f3g1=17
(⃗f∗⃗g)5=f3g2=12(f→∗g→)5=f3g2=12
不想手算?
import numpy as np
from scipy import signal
signal.convolve(np.array([1,2,3,4]),np.array([1,2,3]))
形象化表示
上面的计算过程,可以看作是——
- 把 g 向量的顺序反过来;
- 把 g 的最右一个元素和 f 的最左元素对齐,
- 上下两行都有数字的列相乘(也就是把没有数字的地方看作 0),然后把所有乘积相加,得到 f*g 的第一项;
- 把 g 向右移动一格
- 重复第3、4步
- 直到 g 的最左项移动到 f 的最右一个元素。
形如下列各表:
| f | 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| g | 3 | 2 | 1 | |||
| (f*g)(0) = 1 | 1 |
| f | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| g | 3 | 2 | 1 | ||
| (f*g)(1) = 4 | 2 | 2 |
| f | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| g | 3 | 2 | 1 | |
| (f*g)(2) = 10 | 3 | 4 | 3 |
| f | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| g | 3 | 2 | 1 | |
| (f*g)(3) = 16 | 6 | 6 | 4 |
| f | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| g | 3 | 2 | 1 | ||
| (f*g)(4) = 17 | 9 | 8 |
| f | 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| g | 3 | 2 | 1 | |||
| (f*g)(5) = 12 | 12 |
机器学习的卷积,是卷积吗?
看论文给出的图 Figure 1.1,在卷积核是灰色 3*3 矩阵的情况下,对蓝色 5*5 矩阵的卷积就是直接把核对齐到蓝色矩阵上,并没有把核的元素顺序颠倒过来。
这玩意能叫卷积吗?
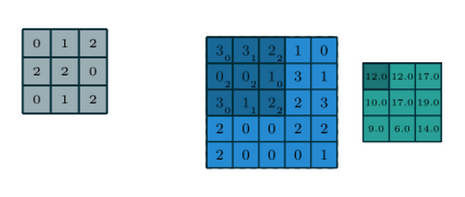
有人强行挽尊,说我们画图示的时候已经把核给颠倒过来了,想知道卷积核就把灰色小矩阵再颠倒回去——
但是,不颠倒就对齐相乘的运算也是有名字的,叫 cross correlation。核有没有颠倒,convolution 还是 cross correlation 一组合,可以带来升维打击般的混乱,堪比高中化学的“还原剂被氧化,氧化剂被还原”……所以,对于计算机专业的数学水平,不予置评~
(你这样纠缠有意思吗?.jpg)
卷积torch.nn.Conv 及其各个参数
in_channels & out_channels
“卷积”的意义在于用一种比较省内存的方式,考虑输入张量中各个元素,和空间上相近的邻居元素之间的关系。所以只需要在真的存在空间关系的维度做卷积,其他维度可以留着不动。
比如一张彩色图片,是一个 (颜色高度宽度) 的 3 阶张量,我们只需要对高度和宽度两个维度做卷积,颜色就是不参与“卷积”的 channel。
in_channel 就是被“卷积”的张量的 channel 数,out_channel 是“卷积”结果的 channel 数。比如我们想从一张 RGB 三色图片中分辨出前景和背景两种不同区域,in_channel=3, out_channel=2。
而 in_channel 如何能够与 out_channel 取值不同,原理见 Figure 1.3。我们使用 out_channel 个不含 channel 维度的“卷积”核,每一个核都与每一个 in channel 做卷积,得到图中的蓝、紫色小矩阵,然后直接把不同的 in channel 暴力求和,得到的结果分别作为卷积结果的 out channel。(这个暴力求和与我以前想得不一样,我以为是什么每一元素都做了一个in_channel*out_channel 的全联通层)
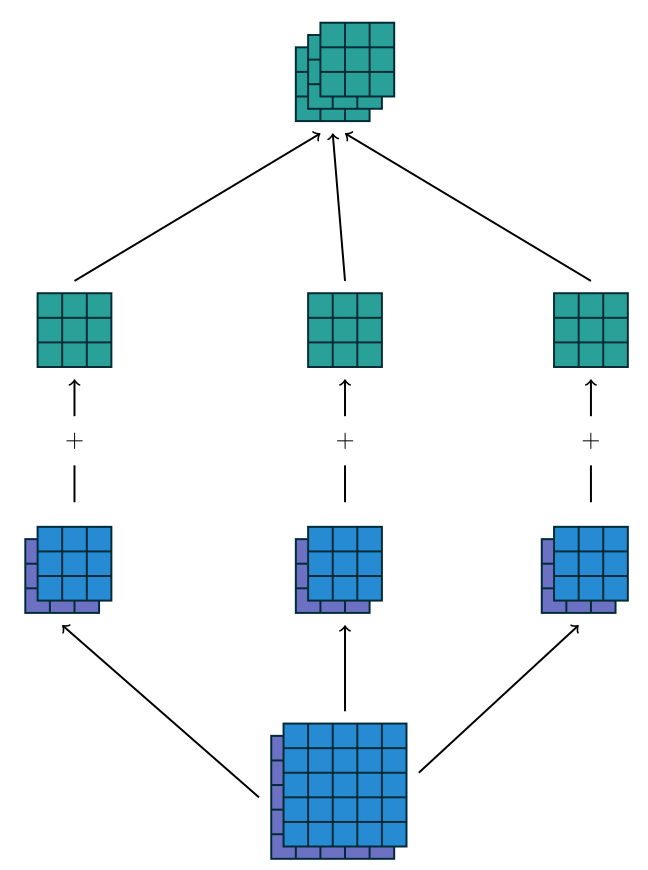
PyTorch 的习惯,对于一个 N 阶“卷积”,参与卷积的是张量的最后 N 阶,in_channel 和 out_channel 也就是被卷张量和卷积结果的 Tensor.shape[-(N+1)]
后面图示的例子都没有考虑 in_channel 和 out_channel 的数量,也就是都当作 1 了。
kernel_size
就是灰色矩阵“卷积”核,每边有几个数字。如果不同方向的边长不一,该参数就需要用一个 tuple 来表示。Figure 1.1 的灰色卷积核,kernel_size=(3,3)
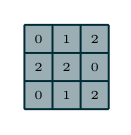
padding & padding_mode
前面手算例子的时候很鸡贼地把 0 作为向量下标的起点。如果采用日常 1 开头的下标来算,第 1 项结果为零,整个卷积结果的长度会长很多,而且多出来的后面几项也都是零。
而且在这个过程中,我们实际上是把一个有限长度的向量,看作了一个以所有整数 \Z\Z 为定义域的函数,除了那有限的几项之外,其余地方都定义函数值为 0。
用计算机计算的话显然没法如此奢侈地谈“无限多个”,例子中实际用到的,在 ⃗ff→ 左右两边各需要 2 个 0,也就是说 padding=2, padding_mode='zeros'
Figure 1.2 表示的就是 padding=(1,1) 的情况(蓝色是被卷张量,白色是 padding,灰色是卷积核,绿色是卷积结果):
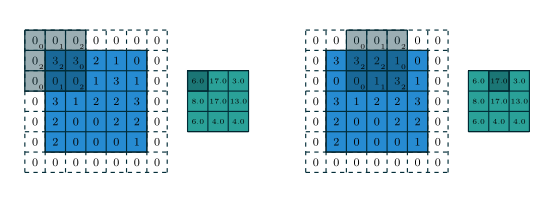
既然神经网络中的卷积并不是真正的卷积,所以他们索性不装了——
正常卷积的结果往往比被卷张量大一圈(具体大多少取决于 kernel_size, padding, stride 多个参数),但是图像处理的时候经常希望输出图片和输入图片一样大,此时可以用字符串 “same” 作为 padding 的参数,自动计算 padding 的大小。“strict” 则表示 padding=0, 这样输出图片尺寸会变小,但是没有 padding,也就没有往图片里掺杂研究者对图片边缘以外信息的臆测。
同时 padding_mode 参数表示往被卷张量四周填充的数字也不一定是 0。比如对于图片,0 往往表示纯黑,而绝大多数图片的视野之外,往往是和图片边缘像素值相差不大的值。所以 padding_mode 除了 zeros 之外,还接受以下取值:
reflect: 以图片边缘为镜面,把边缘附近的像素值对陈反射出去;replicate: 只取边缘的像素值作为常数,直接向外延拓;circular: 类似于物理中的周期性边界条件,取对边附近的像素值作为 padding 内容。
stride
前面手算卷积的第4步,把卷积核向右移动了1格,如果每次移动超过1格,就需要这个参数指定移动步长。如果不同方向的步长不同,也是用 tuple 来表示。
Figure 1.4 表示的就是 stride=(2,2) 的情况(蓝色是被卷张量,蓝色中的深色块是卷积核,绿色是卷积结果):
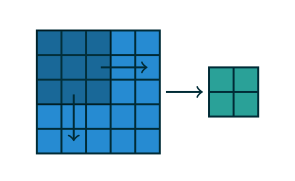
dilation
这个参数把“卷积”核撑开,也就相当于在“卷积”核的相邻元素之间加 0。Figure 1.5 表示的就是 dilation=(1,1) 的情况(蓝色是被卷张量,蓝色中的深色块是卷积核,绿色是卷积结果):
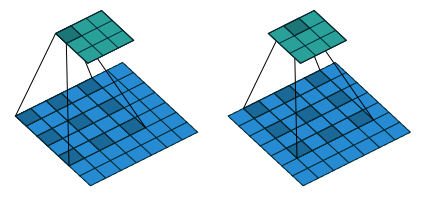
比如 dilation=1 时,(1,2,3) 的卷积核就相当于 (1,0,2,0,3)
比如 dilation=2 时,(1,2,3) 的卷积核就相当于 (1,0,0,2,0,0,3)
这样可以让卷积核在尺寸比较小的情况下,覆盖到更大面积的被卷张量。当然具体实现时,不可能直接补 0 这么浪费内存。
groups
该参数必须是 in_channel 和 out_channel 的公约数,当其不为 1 时,就相当于同时做 groups 个卷积,其中每个卷积的 in_channel=in_channel/groups, out_channel=out_channel/groups
bias
该参数是一个布尔值,卷积类似于一种高维空间里的乘法,这个参数就决定是否要拟合 y=kx+b 中的 b
“卷积”的“逆运算”: TransposeConv
卷积的结果比 padding 之后的被卷张量要小。尤其当“卷积”的 stride 约等于 kernel_size 时,卷积的就变成了某些池化 (pooling)(求最大值不是一种线性算子,所以最大值池化不能用卷积表示,但是平均值池化可以)。
那么在类似 U-net 这样的模型里,右半边的数据升维(下图中的绿箭头),就需要一种“卷积”的“逆运算”。有人把这种运算叫做 deconvolution,有人叫做 transposed convolution,还有人叫做 convolution with fractional strides。
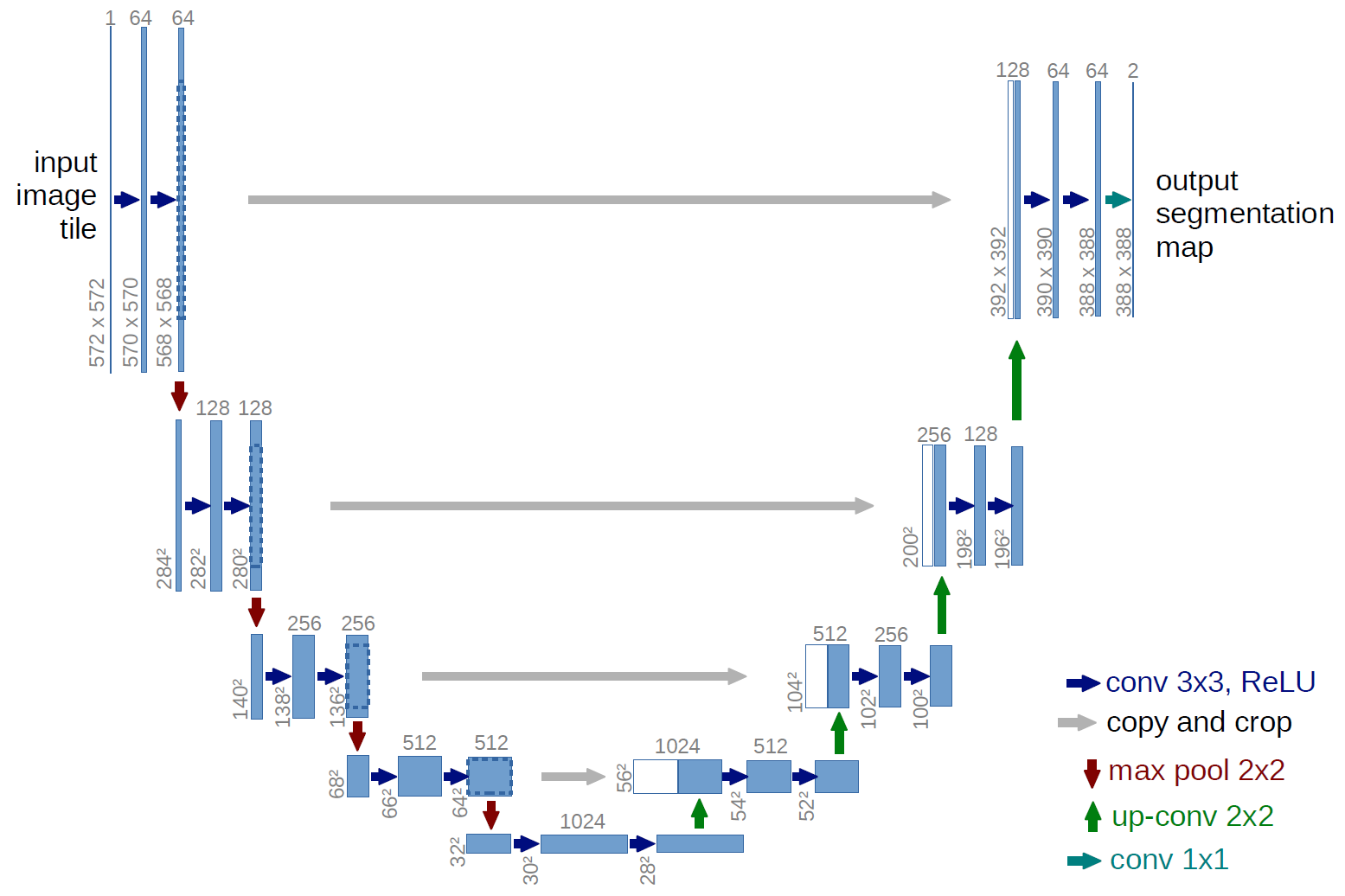
PyTorch 取的是第二种名字。论文解释了为什么这么取名字,笔记以后有时间再补上把……
因为这个与运算本身就是作为“卷积”的逆运算出现的,所以 PyTorch 的文档里这么说:
This is set so that when a
Conv2dand aConvTranspose2dare initialized with same parameters, they are inverses of each other in regard to the input and output shapes.
也就是说,把 ConvTranspose 的输入和输出反过来,然后按照 Conv 的规则确定各个参数,填入 ConvTranspose 的括号里就可以了,除了 output_padding
output_padding
ConvTranspose 的输出就是对应 Conv 的输入。看 Figure 2.7:
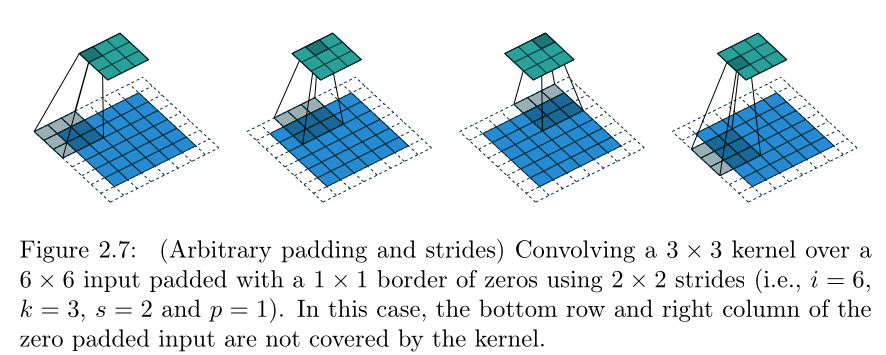
当 (input+2∗padding)/stride(input+2∗padding)/stride 不能整除的时候,最右的几列最下的几行就被卷积核忽略掉了。那么在逆运算 TransposeConv 中,这就意味着同一个输入可能对应着 stride−1stride−1 种可能的输出。output_padding参数就可以消除这种歧义,调整 TransposeConv 输出张量的尺寸。
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK