2

OpenFOAM 编程 | 求解捕食者与被捕食者模型（predator-prey model）问题（ODEs）

 1 year ago
source link: https://www.cnblogs.com/Fitanium/p/16837685.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
neoserver,ios ssh client

0. 写在前面

本文问题参考自文献 [1][1] 第一章例 6，并假设了一些条件，基于 OpenFOAM-v2206 编写程序数值上求解该问题。笔者之前也写过基于 OpenFOAM 求解偏分方程的帖子，OpenFOAM 编程 | One-Dimensional Transient Heat Conduction。

1. 问题描述

假设一群山猫（捕食者）和一群山兔（被捕食者）生活在同一片区域，那么我们可以知道，山猫吃了山兔，繁殖力会增强，山猫的数量会增加。这样一来，山兔的数量会随之减少。接下来，山猫由于食物短缺而数量减少，进而导致山兔遇到山猫的机会减少（被吃掉的概率降低），结果山兔的数量又逐渐增加，这样山猫得到食物的机会也随之增加，其数量又再一次增加，而山兔的数量又会再一次随之减少，如此不断循环。

2. 解析求解

设任意 tt 时刻山兔与山猫的数量分别是 ϕϕ 和 ψψ ，二者的变化服从下面动力学方程

dϕdtdψdt=k1ϕ−μϕψ=νϕψ−k2ψ(1)(1)dϕdt=k1ϕ−μϕψdψdt=νϕψ−k2ψ

其中，k1k1，k2k2，μμ 和 νν 都是正常数。

在上述方程中有几点需要注意：

  1. k1ϕk1ϕ 表示山兔种群的净增长率，与山兔种群数量成正比。
  2. −μϕψ−μϕψ 表示山兔被山猫吃掉而导致的减少率，与乘积 ϕψϕψ （可表示两种动物的相遇概率）成正比。
  3. νϕψνϕψ 表示山猫种群的增长率，由于其数量增长取决于捕食（相遇才有可能），因此 νν 为正值。
  4. −k2ψ−k2ψ 表示山猫种群的死亡率，与其种群数量成正比。

方程组（1）因为含有乘积项，因此是非线性的。现采用线性化的特殊方法求解，即研究种群数量 ϕϕ 和 ψψ 在其稳定值附近的微小涨落。设方程组（1）的稳态解为 ϕ=ϕ0ϕ=ϕ0，ψ=ψ0ψ=ψ0，它们由下面条件决定

dϕdt∣∣∣ϕ=ϕ0,ψ=ψ0dψdt∣∣∣ϕ=ϕ0,ψ=ψ0=0=0dϕdt|ϕ=ϕ0,ψ=ψ0=0dψdt|ϕ=ϕ0,ψ=ψ0=0
k1ϕ0−μϕ0ψ0νϕ0ψ0−k2ψ0=0=0(2)(2)k1ϕ0−μϕ0ψ0=0νϕ0ψ0−k2ψ0=0

代数方程（2）的解为

ϕ0ψ0=k2ν=k1μϕ0=k2νψ0=k1μ

现在，将方程组（1）的解写为下面形式

ϕψ=ϕ0+ξ=ψ0+ηϕ=ϕ0+ξψ=ψ0+η

其中，ξξ 和 ηη 与 ϕ0ϕ0 和 ψ0ψ0 相比都是小量。将上述解带入方程组（1）中可以得到关于变量 ξξ 和 ηη 的方程组

dξdtdηdt=k1ξ−μϕ0η−μψ0ξ−μξη=νϕ0η+νψ0ξ−k2η+νξη(3)(3)dξdt=k1ξ−μϕ0η−μψ0ξ−μξηdηdt=νϕ0η+νψ0ξ−k2η+νξη

其中非线性项 μξημξη 和 νξηνξη 为二阶小量，可以忽略；再将稳态解代入可得线性化的耦合方程组

dξdtdηdt=−k2μνη=k1νμξdξdt=−k2μνηdηdt=k1νμξ

解耦后可得到

d2ξdt2+k1k2ξd2ηdt2+k1k2η=0=0(4)(4)d2ξdt2+k1k2ξ=0d2ηdt2+k1k2η=0

可以知道，式（4）与 L-C 震荡电路及单摆问题同属于相同的数学模型

d2ydt2+k2y=0d2ydt2+k2y=0
y(t)=Esin(kt+δ)    或    y(t)=Ecos(kt+δ)y(t)=Esin⁡(kt+δ)或y(t)=Ecos⁡(kt+δ)

其中，EE 和 δδ 为振幅和初相位，与具体问题有关。

那么我们也可以得到本问题的最终解的形式为

ϕψ=k2ν+E1sin(k1k2−−−−√t+δ1)=k1μ+E2sin(k1k2−−−−√t+δ2)ϕ=k2ν+E1sin⁡(k1k2t+δ1)ψ=k1μ+E2sin⁡(k1k2t+δ2)

其中，每个公式中振幅与初相位取决于各自的初始条件。

3. 数值求解

从上一节可知，我们需要数值求解一个耦合的常微分方程组，可以用RungeKutta法[2][2]。简单推导过程如下：

dϕdtdψdt=f1(ϕ,ψ)=f2(ϕ,ψ)dϕdt=f1(ϕ,ψ)dψdt=f2(ϕ,ψ)
f1(ϕ,ψ)f2(ϕ,ψ)=k1ϕ−μϕψ=νϕψ−k2ψf1(ϕ,ψ)=k1ϕ−μϕψf2(ϕ,ψ)=νϕψ−k2ψ

四阶Runge-Kutta方法可以表示为：

ϕk+1ψk+1=ϕk+Δt6(f11+2f12+2f13+f14)=ψk+Δt6(f21+2f22+2f23+f24)ϕk+1=ϕk+Δt6(f11+2f12+2f13+f14)ψk+1=ψk+Δt6(f21+2f22+2f23+f24)
fi1fi2fi3fi4=fi(ϕk,ψk)=fi(ϕk+Δt2f11,ψk+Δt2f21)=fi(ϕk+Δt2f12,ψk+Δt2f22)=fi(ϕk+Δtf11,ψk+Δtf21)    i=1,2fi1=fi(ϕk,ψk)fi2=fi(ϕk+Δt2f11,ψk+Δt2f21)fi3=fi(ϕk+Δt2f12,ψk+Δt2f22)fi4=fi(ϕk+Δtf11,ψk+Δtf21)i=1,2

求解代码采用 Python 编写，如下所示

#!/usr/bin/python3# -*- coding:utf-8 -*- import numpy as np k1 = 0.7k2 = 0.5mu = 0.1nu = 0.02 def f1(phi,psi): return k1*phi-mu*phi*psi def f2(phi,psi): return nu*phi*psi-k2*psi tStart = 0tEnd = 100.0n = 100000deltaT = tEnd / nhalfDeltaT = deltaT / 2.0Solution = np.ndarray([n+1,2])Solution[0] = [30,20] for i in range(n): f11 = f1(Solution[i][0], Solution[i][1]) f21 = f2(Solution[i][0], Solution[i][1]) f12 = f1(Solution[i][0] + halfDeltaT * f11, Solution[i][1] + halfDeltaT * f21) f22 = f2(Solution[i][0] + halfDeltaT * f11, Solution[i][1] + halfDeltaT * f21) f13 = f1(Solution[i][0] + halfDeltaT * f12, Solution[i][1] + halfDeltaT * f22) f23 = f2(Solution[i][0] + halfDeltaT * f12, Solution[i][1] + halfDeltaT * f22) f14 = f1(Solution[i][0] + deltaT * f11, Solution[i][1] + deltaT * f21) f24 = f2(Solution[i][0] + deltaT * f11, Solution[i][1] + deltaT * f21) Solution[i+1][0] = Solution[i][0] + deltaT / 6.0 * (f11 + 2*f12 + 2*f13 + f14) Solution[i+1][1] = Solution[i][1] + deltaT / 6.0 * (f21 + 2*f22 + 2*f23 + f24) print((i+1)*deltaT,Solution[i+1][0],Solution[i+1][1])

4. OpenFOAM 求解

使用OpenFOAM 数值求解常微分方程（组）主要用到 ODESystem.H（构造微分方程系统）和 ODESolver.H（求解器）；此外，在 OpenFOAM 中需要对常微分方程（组）进行整理[3][3]，进而方便编写代码进行求解。

对于任意阶常微分方程可以转化为一系列一阶常微分方程，这个过程称为降阶，一阶常微分方程的个数与原方程的阶数相等（对于耦合常微分方程组，其阶数等于所有方程阶数之和）。对于某个 nn 阶常微分方程，可按下面形式降阶

y(n)(x)=f(x,y(0),y(1),…,y(n−1))y(n)(x)=f(x,y(0),y(1),…,y(n−1))

其中，nn 为阶数，y(0)=yy(0)=y 。

进一步，引入符号 DD 对各阶导数重新定义，此过程称为转换

Dj=y(j−1)    j=1,2,…,n−1Dj=y(j−1)j=1,2,…,n−1

最终，使用新符号重新表达原系统，此过程称为诱导

D′jD′n=y(n)=Dj+1=f(x,D1,D2,…,Dn)Dj′=Dj+1Dn′=y(n)=f(x,D1,D2,…,Dn)

在 OpenFOAM 中，存在另外一个过程，该过程仅与刚性系统求解器相关，这类求解器需要雅可比矩阵和对自变量的偏导数，即

J=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢∂D′1∂D1∂D′2∂D1⋮∂D′n∂D1∂D′1∂D2∂D′2∂D2⋮∂D′n∂D2⋯⋯⋱⋯∂D′1∂Dn∂D′2∂Dn⋮∂D′n∂Dn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥    和    ∂D′1∂x,∂D′2∂x,,…,∂D′n∂xJ=[∂D1′∂D1∂D1′∂D2⋯∂D1′∂Dn∂D2′∂D1∂D2′∂D2⋯∂D2′∂Dn⋮⋮⋱⋮∂Dn′∂D1∂Dn′∂D2⋯∂Dn′∂Dn]和∂D1′∂x,∂D2′∂x,,…,∂Dn′∂x

接下来，我们看一下如何实现相关求解代码。首先看一下如何构造方程系统。系统代码需要继承 Foam::ODESystem 抽象类，并且需要全部实现三个方法nEqns()、 derivatives() 和 jacobian()，其中 jacobian() 方法对于非刚性求解器可以将实现置空（空函数体）。

让我们重新回顾一下公式（1），可知 nEqns() 应该返回 2；此外， 定义 Y=[ϕ,ψ]TY=[ϕ,ψ]T ，公式（1）可整理成如下向量形式

dYdt=[k1νψ−μϕ−k2]YdYdt=[k1−μϕνψ−k2]Y

因此，导数可按照公式（1）编写即可，只不过需要注意是向量形式。最后，对应之前的描述的降阶过程，可以知道

Y′=f(t,Y)Y′=f(t,Y)

进而可以知道， D1=Y,D′1=Y′D1=Y,D1′=Y′，可得到雅可比矩阵和对自变量的偏导数分别为

∂D′1∂D1=∂Y′∂Y=[k1νψ−μϕ−k2],    ∂D′1∂t=0∂D1′∂D1=∂Y′∂Y=[k1−μϕνψ−k2],∂D1′∂t=0

需要注意的是，雅可比矩阵只有一个元素 ∂D′1∂D1∂D1′∂D1，只不过这个元素是一个块的形式。

具体代码实现如下所示

#include "ODESystem.H" class ODEs : public Foam::ODESystem{public: ODEs() {} ~ODEs() {} // 初始化参数 ODEs(const Foam::scalar k1, const Foam::scalar mu, const Foam::scalar k2, const Foam::scalar nu) { k1_ = k1; mu_ = mu; k2_ = k2; nu_ = nu; } // 方程个数 Foam::label nEqns() const override { return 2; } // 求导 void derivatives(const Foam::scalar x, const Foam::scalarField& y, Foam::scalarField& dydx) const override { // 两个未知量存成向量，y[0] -> \phi, y[1] -> \psi dydx[0] = k1_ * y[0] - mu_ * y[0] * y[1]; dydx[1] = nu_ * y[0] * y[1] - k2_ * y[1]; } // 计算符号的雅可比矩阵和关于自变量的导数 void jacobian(const Foam::scalar x, const Foam::scalarField& y, Foam::scalarField& dfdx, Foam::scalarSquareMatrix& dfdy) const override { dfdx[0] = 0; dfdx[1] = 0; dfdy[0][0] = k1_; dfdy[0][1] = -mu_ * y[0]; dfdy[1][0] = nu_ * y[1]; dfdy[1][1] = -k2_; } private: Foam::scalar k1_; Foam::scalar mu_; Foam::scalar k2_; Foam::scalar nu_;};

对应的，我们实现下主函数

#include <iostream>#include <memory> #include "ODESystem.H"#include "ODESolver.H" class ODEs : public Foam::ODESystem{ // 这里的代码在上边已经介绍，此处省略}; int main(int argc, char* argv[]){ const Foam::scalar startTime = 0.0; // 开始时间 const Foam::scalar endTime = 100.0; // 结束时间 const Foam::scalar phi0 = 30; // 山兔初始值 const Foam::scalar psi0 = 20; // 山猫初始值 const Foam::label n = 100000; // const Foam::scalar deltaT = endTime / n; // 步长 // 系数，参考自文献[4] const Foam::scalar k1 = 0.7; const Foam::scalar mu = 0.1; const Foam::scalar k2 = 0.5; const Foam::scalar nu = 0.02; // 构造对象 ODEs odes(k1, mu, k2, nu); // 构造求解器，具体使用的算法通过参数传递 Foam::dictionary dict; dict.add("solver", argv[1]); Foam::autoPtr<Foam::ODESolver> solver = Foam::ODESolver::New(odes, dict); // 初始化一些变量 Foam::scalar tStart = startTime; Foam::scalarField PhiPsi(odes.nEqns()); // 因变量 PhiPsi[0] = phi0; PhiPsi[1] = psi0; Foam::scalarField ddt(odes.nEqns()); // 保存导数值 // 计算过程 for (Foam::label i = 0; i < n; ++i) { Foam::scalar dtEst = deltaT / 2; Foam::scalar tEnd = tStart + deltaT; // odes.derivatives(tStart, PhiPsi, ddt); solver->solve(tStart, tEnd, PhiPsi, dtEst); // tStart = tEnd; // Foam::Info << tStart << "," << PhiPsi[0] << "," << PhiPsi[1] << Foam::endl; } return 0;}

此外，CMakeLists.txt 文件可参考笔者之前的随笔，如 OpenFOAM编程 | Hello OpenFOAM 和 OpenFOAM 编程 | One-Dimensional Transient Heat Conduction，此处不再赘述。

5. 数据分析

笔者通过命令行参数分别采用RKCK45 算法和 seulex 算法（需要用到雅可比矩阵）对该问题进行求解，从下图可见二者求解得到的结果是一致的。

image

同时运行笔者之前提到的 Python 代码后得到的数值结果与 OpenFOAM 计算结果绘制在同一张图中，二者高度重合。

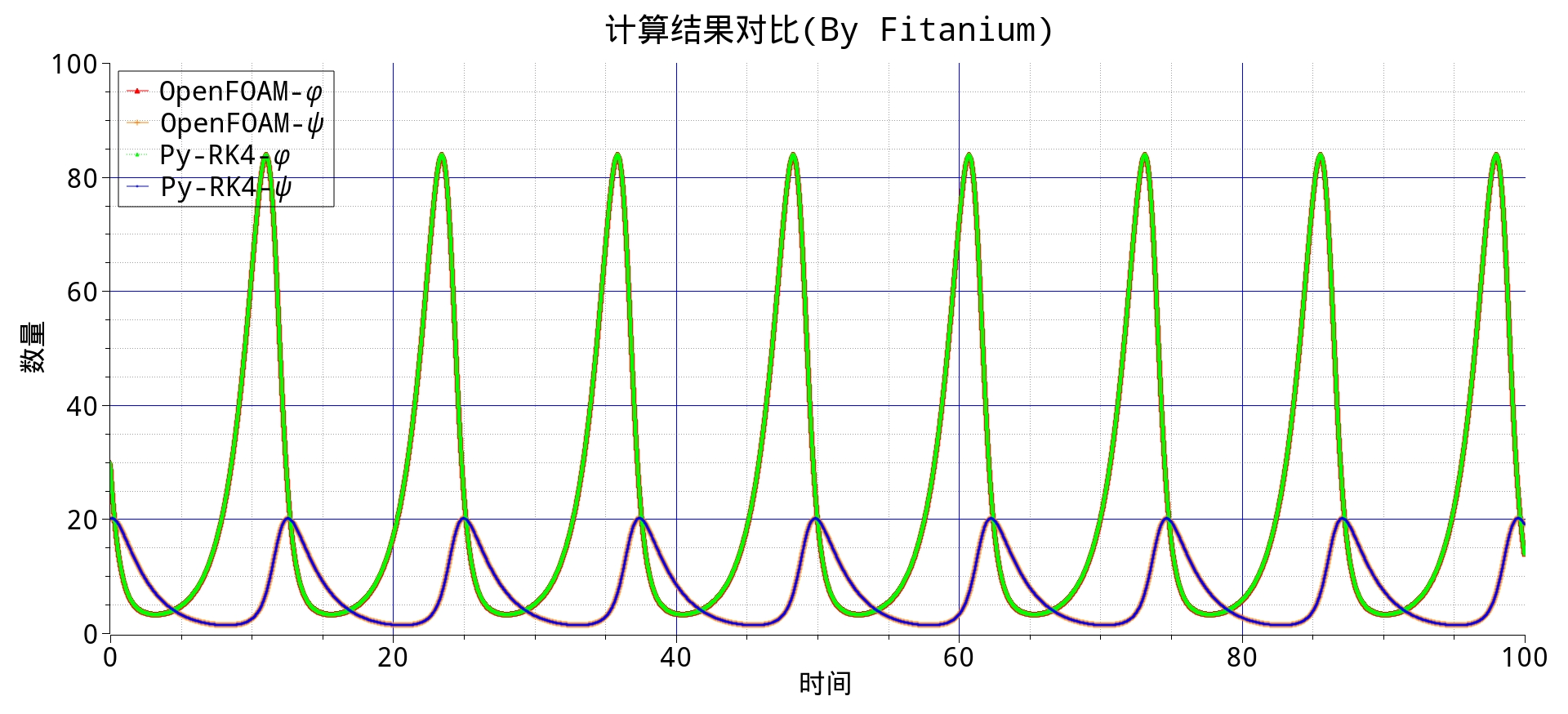
image

同时，解析解法（线性化的特殊解法）得到的结论是二者均按照 k1k2−−−−√k1k2 圆频率震荡，那么对应的周期为 T=2π/k1k2−−−−√=2π/0.7∗0.5−−−−−−−√≈10.62T=2π/k1k2=2π/0.7∗0.5≈10.62，而数值解中得到的周期为 12.425，笔者认为在本文的条件假设下，其中的差距来自于线性解法中没有考虑非线性，但这个解法仍然具有实际意义；读者可以尝试改用绝对值较小的系数来降低其非线性程度。

另外，感兴趣的读者可以尝试使用 Matlab 或 GNU Octave 求解该问题。

[1] 顾樵. 数学物理方法[M]. 北京：科学出版社, 2012.
[2] Chenglin LI.数值计算（四十七）RungeKutta求解常微分方程组
[3] Hassan Kassem. How to solve ODE in OpenFOAM
[4] 捕食者与被捕食者模型——logistic-volterra

防止迷路，请关注笔者博客 博客园@Fitanium。
喜欢的朋友还请点赞、收藏、转发，您的支持将是笔者创作的最大动力。


report

Recommend

About Joyk


Aggregate valuable and interesting links.
Joyk means Joy of geeK