经典背包系列问题

作者：Grey

原文地址：

博客园：经典背包系列问题

CSDN：经典背包系列问题

问题一#

在 n 个物品中挑选若干物品装入背包，最多能装多满？假设背包的大小为m，每个物品的大小为Ai (每个物品只能选择一次且物品大小均为正整数)

题目链接：LintCode 92 · Backpack
​
暴力递归方法思路

定义递归函数

int p(int rest, int i, int[] arr)

递归含义表示：从 i 开始到最后，还剩下 rest 容量的情况下，得到的最大值是多少。

递归函数中有两个决策，第一个决策，不要当前位置物品

int p1 = p(rest, i+1, arr);

第二个决策，要当前物品，这个决策下，有一个限制条件，即当前物品大小不超过 rest，

arr[i] + p(rest - arr[i], i + 1, arr)

暴力解法的完整代码如下

public class Solution {

    public static int backPack(int m, int[] arr) {
        if (arr == null || arr.length < 1) {
            return 0;
        }
        return p(m, 0, arr);
    }

    public static int p(int i, int j, int[] arr) {
        if (j == arr.length) {
            return 0;
        }
        int p1 = p(i, j + 1, arr);
        return i >= arr[j] ? Math.max(arr[j] + p(i - arr[j], j + 1, arr), p1) : p1;
    }
}

优化一，可以通过缓存法来对上述递归过程进行优化，由于递归函数只有两个可变参数，所以可以定义一个二维数组 dp，二维数组的元素全部初始化为 -1，表示未计算过，用这个二维数组就可以存下所有的递归过程中间值，在递归函数中，如果 dp 的值已经计算过，直接返回即可。在每次递归结果返回之前，要先把结果存入 dp 对应的位置，缓存法的完整代码和注释说明如下：

public class Solution {

    public static int backPack(int m, int[] arr) {
        if (arr == null || arr.length < 1) {
            return 0;
        }
        int[][] dp = new int[arr.length + 1][m + 1];
        for (int i = 0; i < dp.length; i++) {
            for (int j = 0; j < dp[0].length; j++) {
                dp[i][j] = -1;
            }
        }
        return p2(m, 0, arr, dp);
    }

    public static int p2(int rest, int i, int[] arr, int[][] dp) {
        // 计算过，直接返回即可
        if (dp[i][rest] != -1) {
            return dp[i][rest];
        }
        int ans = 0;
        if (i == arr.length) {
            // 每次计算的结果在返回之前，先更新 dp 值
            dp[i][rest] = ans;
            return ans;
        }
        int p1 = p2(rest, i + 1, arr, dp);
        ans = rest >= arr[i] ? Math.max(arr[i] + p2(rest - arr[i], i + 1, arr, dp), p1) : p1;
        // 每次计算的结果在返回之前，先更新 dp 值
        dp[i][rest] = ans;
        return ans;
    }
}

优化二，除了上述缓存法，也可以将暴力递归方法直接改成严格位置依赖的动态规划，设置一个 dp 数组

int[][] dp = new int[arr.length + 1][m + 1]

其中 dp[i][j] 就表示递归函数 p(i,j,arr) 的值，根据暴力递归方法可知

dp[i][j] 依赖的位置是 dp[i][j+1] 以及 dp[i - arr[j]][j + 1] 两个位置的值，完整代码如下

public class Solution {

    public static int backPack(int m, int[] arr) {
        if (arr == null || arr.length < 1) {
            return 0;
        }
        int[][] dp = new int[arr.length + 1][m + 1];
        for (int i = arr.length - 1; i >= 0; i--) {
            for (int j = 0; j < m + 1; j++) {
                int p1 = dp[i + 1][j];
                dp[i][j] = j >= arr[i] ? Math.max(arr[i] + dp[i + 1][j - arr[i]], p1) : p1;
            }
        }
        return dp[0][m];
    }
}

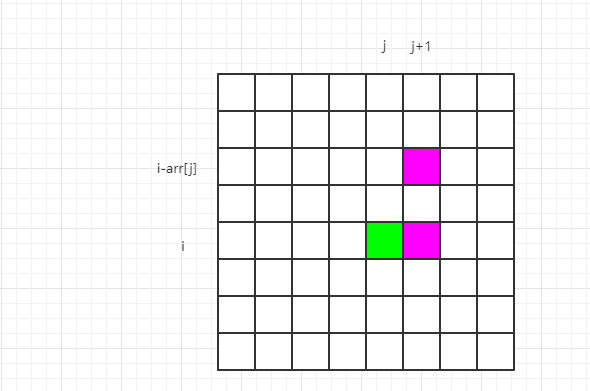
优化三，上述动态规划的转移过程如下

其中 dp[i][j] 依赖的位置是 dp[i][j+1] 以及 dp[i - arr[j]][j + 1] 两个位置，根据这个依赖关系，可以将二维数组简化成一维数组，

设置一维数组

int[] dp = new int[m + 1];

先求最后一列的值，然后复用这个数组推出倒数第二列的值。最后推到第一列的值，完整代码

public class Solution {

    public static int backPack(int m, int[] arr) {
        if (arr == null || arr.length < 1) {
            return 0;
        }
        int[] dp = new int[m + 1];
        for (int i = arr.length - 1; i >= 0; i--) {
            for (int j = m; j >= 0; j--) {
                if (j >= arr[i]) {
                    dp[j] = Math.max(dp[j - arr[i]] + arr[i], dp[j]);
                }
            }
        }
        return dp[m];
    }
}

问题二#

有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值，问最多能装入背包的总价值是多大?

题目链接：LintCode 125 · Backpack II

定义递归函数

int process(int i, int m, int[] w, int[] v)

递归含义表示：i 号及其往后所有的物品在重量允许范围内的最大价值是多少。

首先是 base case

        if (i == w.length) {
            return 0;
        }

表示无物品可选，返回 0 的价值。

接下来是普遍情况，有两种决策，

决策一：选择 i 位置的物品，则

int p1 = process(i + 1, m, w, v);

决策二，不选择 i 位置的物品，此时有条件，即物品重量不能超过当前书包的剩余容量，即

v[i] + process(i + 1, m - w[i], w, v)

完整代码如下

public class Solution {

    public static int backPackII(int m, int[] w, int[] v) {
        if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
            return 0;
        }
        return process(0, m, w, v);
    }

    // i号及其往后所有的物品在重量允许范围内的最大价值是多少
    public static int process(int i, int m, int[] w, int[] v) {
        if (i == w.length) {
            return 0;
        }
        // 不选i号商品
        int p1 = process(i + 1, m, w, v);
        if (m >= w[i]) {
            // 这种情况下，才有资格选i号商品
            return Math.max(p1, v[i] + process(i + 1, m - w[i], w, v));
        }
        return p1;
    }
}

优化一，增加缓存，使用一个二维数组 dp 来存储递归过程的中间值

int[][] dp = new int[w.length + 1][m + 1];

dp 的初始值全为 -1， 同时，将每次递归结果都存入 dp 中，如果某个递归算过了，则直接返回即可，完整代码如下

public class Solution {

    public static int backPackII(int m, int[] w, int[] v) {
        if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
            return 0;
        }
        int[][] dp = new int[w.length + 1][m + 1];
        for (int i = 0; i < dp.length; i++) {
            for (int j = 0; j < dp[0].length; j++) {
                dp[i][j] = -1;
            }
        }
        return process2(0, m, w, v, dp);
    }

    public static int process2(int i, int m, int[] w, int[] v, int[][] dp) {
        if (dp[i][m] != -1) {
            return dp[i][m];
        }
        if (i == w.length) {
            dp[i][m] = 0;
            return 0;
        }
        // 最后一行都是0
        // 从最后一行开始
        int ans = process2(i + 1, m, w, v, dp);
        if (i < w.length && m >= w[i]) {
            // 这种情况下，才有资格选i号商品
            ans = Math.max(ans, v[i] + process2(i + 1, m - w[i], w, v, dp));
        }
        dp[i][m] = ans;
        return ans;
    }
}

优化二，由于暴力递归过程只有两个可变参数，所以本问题也可以改成严格位置的动态规划解，定义一个二维数组 dp，

int[][] dp = new int[w.length + 1][m + 1];

通过观察暴力递归过程可知，dp[i][j] 依赖 dp[i+1][j] 和 dp[i+1][j-w[i]] 两个位置的值，完整代码如下

public class Solution {

    public static int backPackII(int m, int[] w, int[] v) {
        if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
            return 0;
        }
        int[][] dp = new int[w.length + 1][m + 1];
        // 倒数第一行都是0
        // 从倒数第二行开始填
        for (int i = w.length - 1; i >= 0; i--) {
            for (int j = m; j >= 0; j--) {
                dp[i][j] = dp[i + 1][j];
                if (j >= w[i]) {
                    dp[i][j] = Math.max(dp[i][j], v[i] + dp[i + 1][j - w[i]]);
                }
                if (j == m && i == 0) {
                    break;
                }
            }
        }
        return dp[0][m];
    }
}

优化四，参考问题1，上述动态规划也可以做进一步的空间压缩，使用一个一维数组来滚动更新，不赘述，完整代码如下

public class Solution {

        public static int backPackII(int m, int[] w, int[] v) {
        if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
            return 0;
        }
        int[] dp = new int[m + 1];
        for (int i = w.length - 1; i >= 0; i--) {
            for (int j = m; j >= 0; j--) {
                if (j >= w[i]) {
                    dp[j] = Math.max(dp[j], v[i] + dp[j - w[i]]);
                }
                if (i == 0) {
                    break;
                }
            }
        }
        return dp[m];
    }
}

更多#

算法和数据结构笔记