数值分析<3>——任意曲线拟合

万物皆是展开式

你是否想过这样一个问题，任何的函数，也许都能通过一个“大一统”理论将他们整合在一起。事实上对于任意一种对应关系，我们都能找到一个函数尽可能去贴合它，我们采取的是一种极限的思维，举个不恰当的例子来描述，如果一个东西看起来像牛粪，闻起来像牛粪，尝起来像牛粪，那么它就是牛粪。并且，更加一般的是，在一个微小的区间内，函数还可以写成一个幂函数的形式去大致的估算。

泰勒定理给了我们一个很通用的方法去研究函数：

设n是一个正整数。如果定义在一个包含a的区间上的函数f在a点处n+1次可导，那么对于这个区间上的任意x，都有：

f(x)=∑i=0nf(i)(a)i!(x−1)i+Rn(x)

其中，上式的Rn(x)是泰勒公式的估计余项，这在后续会进行详细的解释。

如果仅仅只是背下来，你就不能领略到泰勒展开的精妙之处了。我们用一些很精妙的手段，自然的推导出泰勒公式。首先我们先假定一个函数存在一阶导函数，来看一看一阶导数的定义

limx→x0f(x)−f(x0)x−x0=f′(x0)

其实从这里不难发现，导数定义上，给了我们一种当x→x0的时候，计算f(x)的手段，我们假定这个过程的无穷小为α(x)(x→x0)，那么我们可以把这个等式改写为如下形式

limx→x0=f(x)=L⇔f(x)=L+α(x)limx→x0f′(x)=f(x)−f(x0)x−x0=f′(x)+α(x)f(x)=f(x0)+f′(x0)(x−x0)+α(x)×(x−x0)=f(x0)+f′(x0)(x−x0)+ο(x−x0)

从上面的推导规程很明显可以看出最后一项无穷小是(x−x0)的高阶无穷小，所以我们就很自然的得出了f(x)的一阶泰勒展开式。利用这个公式，我们可以去拟合任意可导的函数的任意函数点，再从点的绘制成函数曲线。

当然我们会认为，一阶导数所带来的那个余项无穷小是不够精确的，提高精确值的方法就是让这个无穷小的阶升高，那么我们可以继续考虑二阶展开，让这个无穷小的阶数升高。首先我们来单独的研究一下这个无穷小。

ο(x−x0)=f(x)−f(x0)−f′(x0)(x−x0)limx→x0ο(x−x0)(x−x0)2=limx→x0f(x)−f(x0)−f′(x0)(x−x0)(x−x0)2

很明显，只要我们的函数二阶可导，那么上述式子就满足了0/0型的洛必达法则！那么我们直接开始洛必达！

limx→x0f(x)−f(x0)−f′(x0)(x−x0)(x−x0)2=limx→x0f′(x)−f′(x0)2(x−x0)=12f″(x0)=limx→x0ο(x−x0)(x−x0)2⇔ο(x−x0)=12f″(x0)(x−x0)2⇔f(x)=f(x0)+f′(x0)(x−x0)+12f″(x0)(x−x0)2+ο(x−x0)2

这样，我们就得到了拥有二阶无穷小的泰勒公式！如法炮制，只要我们的f(x)在x0满足n阶可导的情况，那么我们就可以一直用上面的方式得到n阶泰勒展开公式。

接下来我们来估计余项，也就是误差的大小。在上面的推断中，我们一直使用无穷小进行误差的估计，这种类型的余项叫做皮亚诺余项，这种好处是可以很直观的看出误差的阶数，但是并不算是一个特别容易计算的值，我们仅仅知道最大的误差不超过ο(x−x0)n。因此我们可以思考一下，假如我们展开到第n阶的时候，误差必然是比第n+1阶新引入的那一项更大，但比第n阶是更小的，那么我们可以用介值定理和拉格朗日微分中值定理进行推广，那么余项可以写成

Rn(x)=f(n+1)(θ)n!(x−x0)n+1

利用泰勒公式，我们就可以将一个可导函数的任意点进行一个拟合，从而得到一个较为精确的结果，从函数图像上看，泰勒公式是一个级数累加不断前进逼近的过程。

多项式插值法

如果针对的是一个有穷数列，例如请你寻找以下数字的规律并填写接下来的数字

4、7、11、18、29、47、(__)

你的第一眼可能会发现这是一个类似 Fibonacci数列的规律数字，但实际上我们对于有穷离散型函数，也可以推出这样一个奇怪的对应关系

ax=28579x990720−142847x810080+4140931x715120−713627x6240+17192243x5864−40631363x4480+644406697x32835−927568429x22520+101426987x315−113739

并且对于任何的有穷的数列，我们总是能使用一个通项公式进行数据的拟合计算。如果我们把上述拓展到函数领域，也就是对于任意有限多的(xi,yi)，且这些点符合函数的规则，每个x对应唯一的y，我们总能用一个连续的多项式组合的函数，保证这个函数经过上面所有的点，而计算这个多项式的过程，我们就称为插值。插值是求值的逆过程，利用已有的点，反推出曲线的大致模样。

插值的思想和泰勒很类似，就是说如果观测误差足够小的时候，那么就认为它就是准确的值。我们给定的点符合f(xi)=yi，那么我们的插值构造函数就是g(xi)=yi。

通常我们采用累加的多项式进行插值计算，因为我们的计算都是建立在计算机之上，计算机对于特殊的运算是非常缓慢且复杂的，例如之前提到的泰勒展开，因此我们尽可能需要将计算变成四则运算，同时我们的插值函数还需要保证解的唯一性，因此我们通常将插值函数写成如下形式：

P(x)=∑i=0naixi

利用多项式幂函数和作为插值函数的好处是，它是恒可微的，并不需要像泰勒展开一样，需要先确定可微分的函数才可以继续求解。同时至于这种方式的唯一性，我们可以做一个简单的推导。

假设给定了n+1个数据采样(x1,y1),(x2,y2)⋯(xn+1,yn+1)，根据插值法的规则，那么我们构造出的多项式必然满足下列方程组：

{p(x0)=a0+a1x0+a2x02+⋯+anx0n=y0p(x1)=a0+a1x1+a2x12+⋯+anx1n=y1p(x2)=a0+a1x2+a2x22+⋯+anx2n=y2⋮p(xn)=a0+a1xn+a2xn2+⋯+anxnn=yn

如果熟悉线性代数，我们可以很清楚的发现这是一个非齐次线性方程组（a为未知数），我们可以得到该方程组的Vandermonde行列式

P=VA=Y⇔[1x0x02⋯x0n1x1x12⋯x1n⋮⋮⋮⋮⋮1xnxn2⋯xnn][a0a1⋮an]=[y0y1⋮yn]

|V|=|1x0x02⋯x0n1x1x12⋯x1n⋮⋮⋮⋮⋮1xnxn2⋯xnn|=∏i=1n∏j=0n(xi−xj)

因为我们取得采样点都是不同的点，因此可以保证有xi≠xj，那么根据Cramer法则，该Vandermonde行列式必有唯一解，从而保证了我们的插值函数是唯一的。不过多项式插值也不是全无缺点的，计算复杂度较高、在端点出容易出现龙格现象（一种函数值的剧烈振荡）。这些问题我们将在后面进行讨论。

拉格朗日插值法

拉格朗日插值是一种朴素拟合的手段，假设我们给定n个数据点(x1,y1),(x2,y2)⋯(xn,yn)，拉格朗日插值法，就是构造一条经过这些点的曲线（如果本身的数据就存在大量误差，则只需要靠近而不需经过），用这条线去模拟实际的曲线。这个方法和我们通过两点构造一条直线的方法有异曲同工之妙，当我们代入一个值x1之后，所有不能得到y1的多项式都将系数为0。

一次线性插值

我们先从最容易的一次线性插值来入手，假设我们有曲线f(xi)=yi，取两个采样点x(x0,y0),(x1,y1)，我们一次线性插值则是使用一条直线来近似替代，那么我们需要构建一个函数，使得p(x0)=y0,p(x1)=y1，那么可以作出这样一条直线（直线对称式）：

p(x)=x−x0x0−x1y0+x−x1x1−x0y1

我们看一个简单的函数拟合，已知y=x的两个采样点(100,10),(121,11),求115，我们利用线性插值法，可以计算出结果是10.7142，精确值为10.724，可见利用线性插值也具备三位有效数字。但是如果将值偏离采样点，例如我们需要计算2，精确值为1.414，而插值法计算出的值为5.333，一位有效数字都没有。

实际上我们利用信息的角度去考虑，比如在警察办案过程中，往往会涉及到一个犯罪嫌疑人画像的制作，如果说目击者告诉警察的有效信息为：犯罪分子是一个高鼻梁，蓝眼睛。那么警察在绘制图像的时候，眼睛和鼻子或者周边的颧骨可能会相对精确不少，但是通过鼻子和眼睛的信息，你让警察去猜想他是否是秃顶或者升高体重，自然会不准确。所以这里面也涉及到了一部分信息熵的内容，因为信息过少而导致的数据不精确。

拉格朗日插值

通过一次插值的实践过程和之前对于多项式插值的，我们知道采样点很少导致的信息缺失，那么我们就应该找到更多的采样点进行构造更好的多项式。

根据观察，其实我们可以思考一下，之前多项式插值法中，我们最终是需要通过行列式解出各个多项式的系数，那么我们假定为这样的插值函数

p(x)=∑i=0nli(x)yi

我们将多项式系数写为l(x)我们称为拉格朗日插值基函数。这个基函数必然满足

p(xi)=yili(xk)={0,k≠i1,k=0

通过这个我们很容易分析出插值基函数li(x)有零点xi，其他的均为非零点，那么我们假设插值基函数为：

li(x)=C∏k=0,k≠in(x−xk)

同时因为li(xi)=1可以继续确定常系数

C=1∏k=0,k≠in(xi−xk)

因此我们得到了我们的插值基函数和我们的插值拟合函数

li(x)=∏k=0,k≠ix−xkxi−xkpn(x)=∑i=0nli(x)yi=∑i=0n(∏k=0,k≠inx−xkxi−xk)×yi

因此，我们可以编写出一程序，作为我们拉格朗日插值法的

double[] Lagrange(double[]x,double[] y,double[] xi)
{
    double[] result = new double[xi.Length];
    if (x.Length != y.Length)
    {
        throw new ArgumentException("dim x not equal dim y");
    }
    int n = x.Length;
    for (int k = 0; k < xi.Length; k++)
    {
        double value = 0;
        for (int i = 0; i <n; i++)
        {
            double mulValue = 1;
            for (int j = 0; j < n; j++)
            {
                if (i == j)
                    continue;
                mulValue = mulValue * (xi[k] - x[j]) / (x[i]- x[j]);
            }
            value += mulValue * y[i];
        }
        result[k] = value;
    }
    return result;
}

更有matlab、python版本的代码在仓库中可以对照使用。仓库地址见文章开头

*拉格朗日插值余项

既然是拟合，总归是有误差的，接下来我们研究一下最终的误差。对于拉格朗日插值法，误差实际上是一个阶段误差R(x)=f(x)−p(x)，根据之前我们推导出的拉格朗日插值函数，误差余项记为R(x)=f(x)−p(x)。

那么我们作一辅助函数如下

φ(t)=f(t)−p(t)−g(t)g(x)[f(x)−p(x)]g(x)=∏i=0n(x−xi)

容易发现gn+1(t)=(n+1)!，而插值函数只有n阶，故pn+1(t)=0，因此我们构造的辅助函数是连续且具有n+1阶导数。当t=x时，则会有φ(t)=0，根据Rolle定理，则必有以下：

当φ(t)在插值区间内有n+2个互异零点时，则一阶导数至少有n+1个互异零点
当φ(1)(t)在插值区间内有n+1个互异零点时，则φ(2)(t)至少有n个互异零点

以此类推，容易知道φ(n)(t)有2个零点时，则φ(n+1)(t)至少有一零点，设此零点为t=ξ，对φ(t)求n+1次导数后，有

φ(n+1)(ξ)=f(n+1)(ξ)−(b+1)!g(x)[f(x)−p(x)]=0

故我们插值的截断误差为f(x)−p(x)=fn+1(ξ)(n+1)!∏i=0n(x−xi)，其中ξ取决于我们需要预测的值。自此，我们得到了拉格朗日插值法的所有内容。

Newton差商插值

拉格朗日插值多项式的得出并不容易，至少在计算机眼中，他是复杂的，需要计算多个n-1阶的多项式。同时，这里我们给出一个定理：所有的插值多项式和拉格朗日插值多项式的结果应当是相同的，只是以不同的方式计算和书写。。

首先我们介绍以下差商的概念，实际差商是一个很简单的东西，定义如下：假设顺序排列的节点x0,x1,⋯,xn对应函数值为f(x0),f(x1),⋯,f(xn)，那么一阶差商为

f[x0,xk]=f(x0)−f(xk)x0−xk,(1<=k<=n)

二阶差商为

f[x0,x1;x2,xk]=f[x0;x1,x2]−f[x0;x1,xk]x2−xk,(2<=k<=n)

那么K阶差商为：

f[x0,x1,⋯;xk−2,xk−1]=f[x0,x1⋯;xk−2,xk−1]−f[x0,x1⋯xk−2,xk]xk−1−xk,(k<=n)

k阶差商亦可写成

f[x0,x1,⋯,xk−1,xk]=f[x0,x1,⋯,xk−1]−f[x0,x1,⋯,xk−1,xk]x0−xk

实际上就是个递推的公式，看起来似乎很复杂，但实际上自己尝试去计算的时候会发现，是一个很简单的东西，同时差商是函数的一个线性组合，这又可以说到线性代数了，我们假设组合出的多项式是一个类似坐标的玩意，而每一阶的差商实际上就是向量的基，因此通过差商，我们可以表示出多项式空间中任一多项式。

牛顿差商公式

牛顿差商公式就是将我们的差商做出组合：

P(x)=f[x1]+f[x1,x2](x−x1)+f[x1,x2,x3](x−x1)(x−x2)+⋯+f[x1⋯xn](x−x1)⋯(x−xn−1)

随便给出几个插值采样点，进行计算拉格朗日和牛顿插值公式，我们在计算出各阶差商以后，会发现最终得到的插值多项式和拉格朗日多项式是一致的。那我们为什么还需要多此一举引入牛顿法进行插值而不是直接使用拉格朗日插值呢？

答案很简单，拉格朗日法在构建多项式时，我们必须先知道采样点的数量，如果后续有了新的采样点，我们就需要重新计算整个多项式，这是对于性能浪费极大的。如果采用牛顿法，那么在有新的采样点时，我们只需要多计算一次差商（因为之前的差商已经计算好），可以很容易的将新的点加入我们的多项式中。

牛顿法的代码如下（更多代码见仓库）

double Newton(double[] x, double[] y,double xi)
{
    if (x.Length != y.Length)
    {
        throw new ArgumentException("dim x not equal dim y");
    }
    int n = x.Length;
    double[,] args = new double[n,n];
    for (int i = 0; i < n; i++)
    {
        args[i,0] = y[i];
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = i; j <= n; j++)
        {
            args[j,i] = (args[j - 1,i - 1] - args[j,i - 1]) / (x[j - i] - x[j]);
        }
    }
    double result = y[0];
    for (int i = 1; i < x.Length; i++)
    {
        double mulValue = 1.0;
        for (int j = 0; j < i - 1; j++)
        {
            mulValue = mulValue * (xi - x[j]);
        }
        result += args[i, i] * mulValue;
    }
    return result;
}

实际上，牛顿法因为得到的结果和拉格朗日插值一样，他们的误差也应该是一样的，不过既然我们选择了不同的计算方法，那么误差也可以使用新的手段进行计算。如果我们把我们的插值点看作一固定点，带入我们的差商公式，依次递推，会得到最后的插值余项。

R(x)=f[x0,x1⋯,xn,x](x−x0)(x−x1)⋯(x−xn)

高次插值的Runge(龙格)现象

在多项式插值以及基于多项式插值的拉格朗日插值方法和含有高次幂的牛顿插值中，我们提到过龙格现象，那么什么是龙格现象呢？首先我们先提出这样一个问题，当我们在拉格朗日多项式之中提高项数和多项式的次数，是否可以提高我们数据的精度？这个答案是否定的，我们需要减少误差，也就是说针对任意的ϵ>0，总是存在正整数N，当n大于N时，所有区间内的x满足:

f(x)−pn(x)<ϵ⇔fn+1(ξ)(n+1)!∏i=0n(x−xi)<ϵ

我们可以看到，我们的误差，随着n的增大，(n+1)!逐渐趋于无穷，而后向的乘法，并不会增大太多会变小太多，因此误差很大程度取决于n+1阶导数的范围。对于类似sinx,ex，这类导数的值域范围恒定的函数，误差会随着n的增加逐步趋于0。但是如果对于某些函数而言，随着项数次数增加，误差反而会变大。龙格现象是一种出现在多项式次数很高是，在区间端点出现拟合曲线剧烈振荡的一种现象。下面通过一个例子来进行说明。

假设给定f(x)=1x2+1,x∈[−5,5]，等距离取5，10个点，构建多项式拟合，观察图像。

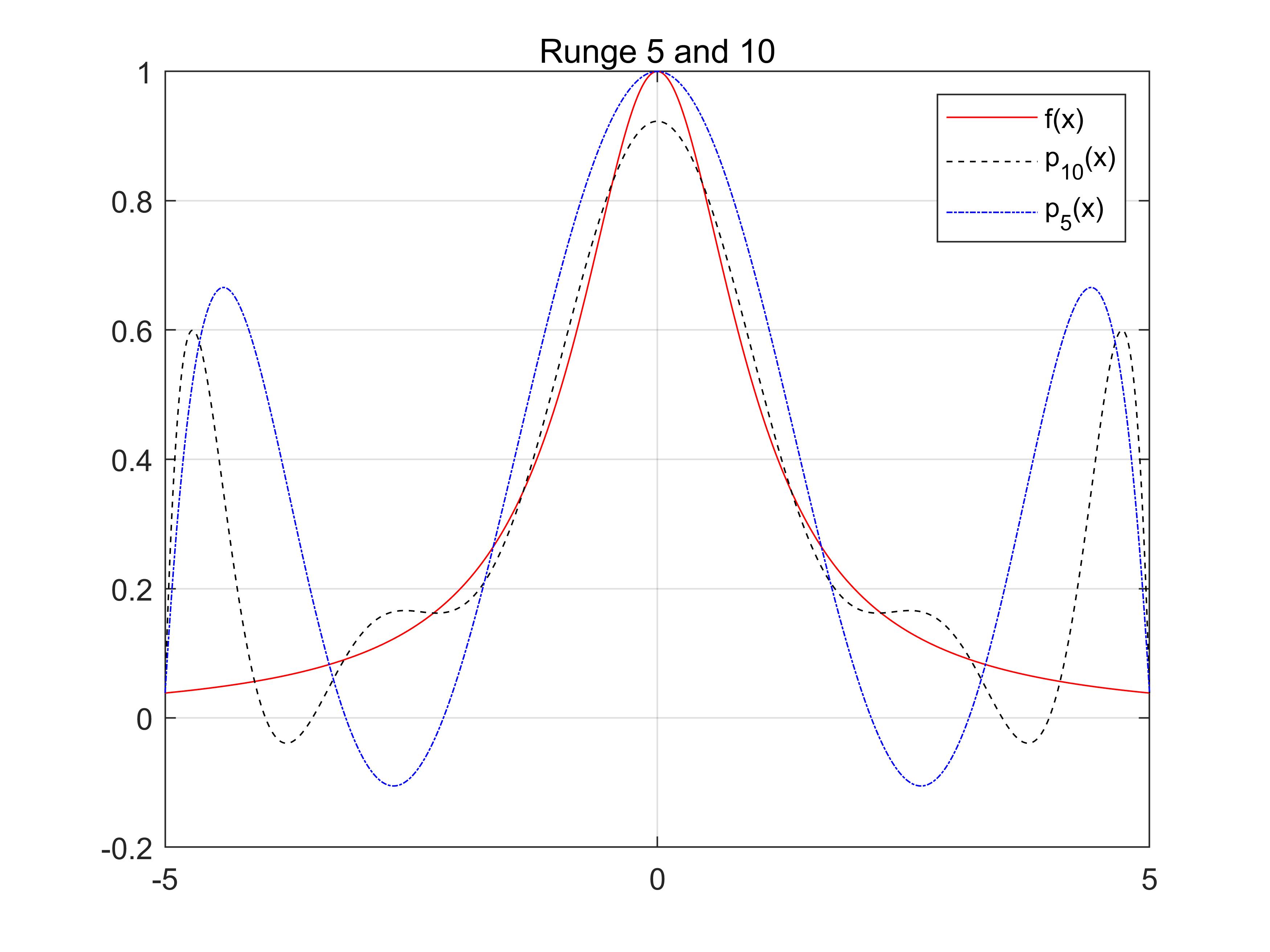
我们可以很清楚的发现，当靠近端点的时候。拟合曲线出现了剧烈的波动，误差到了一个不太可以接受的程度。并且次数越高的时候，抖动出现的更频繁、更剧烈。龙格现象的出现是由于插值节点是等距所造成的。同时，针对导函数不稳定的函数而言，盲目增加插值节点数列，则更加容易出现龙格现象。

一般而言，为了避免龙格现象，我们可以有以下的手段：

避免使用高次的插值多项式，一般而言，即使为了提高插值精度，也尽可能保证n<7。
分段进行插值，在每一小段使用一次插值，从而降低阶数。
对于性态不稳定的函数，选用其他插值手段，如Hermite插值等。

Hermite插值

在之前的插值方法中，我们的要求仅仅是在满足f(x)=p(x)或者两者足够接近作为一个条件，但是这并不足以做出完美的拟合，在许多时候，我们往往还会要求导数及高阶导数尽可能相同或接近，这种拓展了条件的插值方法，就是我们的Hermite插值方法。

最常见的是我们通常会要求曲线的一阶导数接近或相同，这样可以保证我们曲线的一个平滑性能。那么假设曲线y=f(x)，一阶导数为y′=f′(x)，那么Hermite插值需要保证：

{H(xi)=yH′(xi)=y′

不难发现，我们不仅要求了相等的条件，更是要求了相切的条件，因此上述公式具有2(n+1)个采样点（曲线和曲线导数各一半）,那么我们仿造拉格朗日插值条件。可以构造一个这样的插值多项式：

H(x)=a0(x)y0+b0(x)y0′+⋯+an(x)yn+bn(x)yn′=∑i=0n(aiyi+biyi′)

其中，需要满足：

{ai(xk)={0,k≠i1,k=iai′(xk)=0

{bi(xk)={0,k≠i1,k=ibi′(xk)=0

接下来我们用比较长的篇幅证明推导以下我们的Hermite插值的基函数a(x),b(x)，以及证明他的唯一性。

首先我们来求b(x)，它需要满足

bi(xk)=bi′(xk)=0,i≠k

易知满足上述条件的该点为二重根，所以必有因子(x−xi)2,i≠k，

bi(xk)=0,bi′(xk)=1,i=k

易知满足上述条件的该点为单根，因此还会有另一个因子，(x−xi),i=k。又因为b(x)是次数不超过2n+1的多项式，根据拉格朗日多项式的定义，可以假定

bi(x)=C(x−xi)li2(x)

上述式子满足我们之前的规定，同时因为bi′(x)=1，可以轻松的确定常系数为1。故bi(x)=(x−xi)li2(x)。接下来可以确定一下a(x)。

同样的，因为a(x)=0,ai′(x)=0,i≠k说明也具有二重根，同样基函数会含有（（x−xi)2,i≠k，但略微不同的是，k=i的时候，P我们不能在获得任何因子凑够2n+2项。因此我们利用待定系数法假定基函数为

ai(x)=(ax+b)li2(x)

同样代入我们的条件，最终可以求得：

ai(x)=(1−2(x−xi)∑k=0,k≠in1xi−xk)li2(x)

最后我们证明一下我们得到的插值多项式是唯一的，我们利用反证法：

假设存在另一个h(x)是满足Hermite插值条件，那么设：

φ(x)=H(x)−h(x)=0φ′(x)=H′(xi)−h′(xi)=0

由于有n+1个i，因此φ(x)有2n+2个零点，但是φ(x)=H(x)−h(x)=0次数不超过2n+1，所以φ(x)=0，因此H(x)=h(x)，该多项式唯一。

Hermite插值余项

若我们的函数f(x)在插值区间上2n+2阶导数，那么我们假设余项为R(x)=f(x)−H(x)，由Hermite插值定义可知，xi是R(x)的二重根，因此R(x)含有(x−xi)，那么设

R(x)=k(x)∏i=0n(x−xi)2

做出辅助函数

φ(x)=f(t)−H(t)−R(x)

根据定义易知

φ(xi)=0,φ′(xi)=0,φ(x)=0

因此辅助函数至少有n+1个二重零点x_i，以及零点x，根据罗尔定理，容易知道在每两个二重零点之间都有一个零点，同时φ′(xi)=0，φ′(t)至少有2
n+2个零点，以此类推，那么有

φ(2n+2)(ξ)=f(2n+2)ξ)−(2n+2)!k(x)k(x)=f(2n+2)ξ)(2n+2)!

所以余项公式为：

f(x)=f(2n+2)ξ)(2n+2)!∏i=0n(x−xi)2

Hermite的代码如下（更多代码见仓库）

Chebyshev插值

我们之前谈论的插值函数通常采样点是一个平均分布的采样点，比如说我们一个实际的例子，我们需要采集子弹发射速度，我们往往会使用等间隔时间发射一颗子弹。但是往往等间隔这件事情本身就是有难度的，也就是说我们选取的点对结果是有影响的，如下图，在端点的时候，误差可能会达到一个无穷大的地步。切比雪夫插值就是采用最优点间距选取的插值方法。

切比雪夫插值的出发点就是在插值区间上，控制插值误差的上下界，即

∏1n(x−xi)n!f(n)(ξ)

将这个误差控制在绝对值为1以内，实际上这是一个关于x的多项式，那么我们的问题就是，这个多项式是否存在极值，是否有特定的xi使得最大值足够的小呢？那么我们试着列出公式进行推导：

min(max1⩽x⩽1|∏i=1i=n(x−xi)|)

我们再考虑一个问题，我们既然要构造多项式，并且控制误差在1以内，那么考虑一下三角函数，因为三角有两个优秀的性质：

三角函数的值域在[−1,1]
根据傅里叶展开，我们知道曲线可以用三角函数进行拟合

因此如果区间在[−1,1],我们选择xi=cos(2i−1)π2n（如果区间为[a,b]，那么选取xi=b+a2+b−a2cos(2i−1)π2n），这样xi最小值就是1/2n−1。我们可以看看切比雪夫根构造的插值采样点和普通的插值采样点构造的函数有何区别：

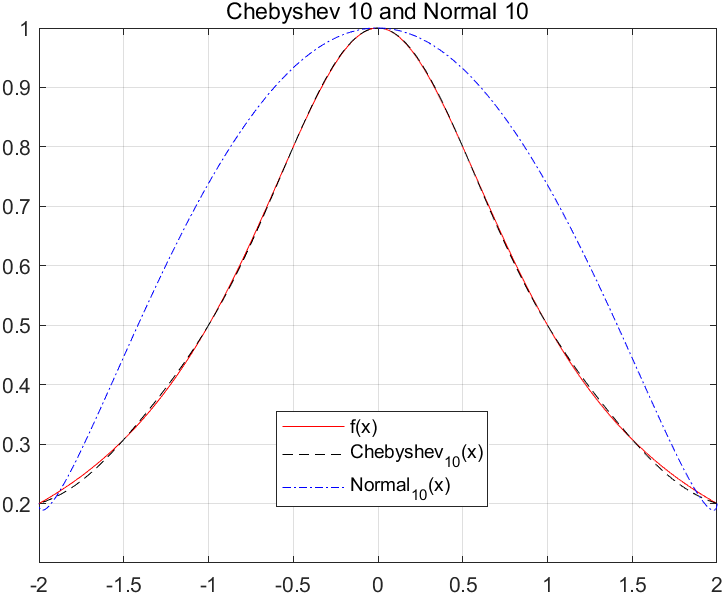
我们利用切比雪夫根（建议学习切比雪夫微分方程），构造的多项式就是切比雪夫多项式，在此之前，我们看一看三角函数的展开：

cos(2θ)=2cos2θ−1cos(3θ)=4cos3θ−3cosθcos(4θ)=8cos4θ−8cos2θ+1

通过观察，那么我们假设g(cosθ)=cosnθ，g(x)是一个多项式，系数为2n−1。实际上这也是成立的，证明过程留给读者。那么我们令切比雪夫多项式公式为：gn(cosθ)=cosnθ
，于是：

gn+1(cosθ)=cos(nθ+θ)=cosnθcosθ−sinnθsinθgn−1(cosθ)=cos(nθ−θ)=cosnθcosθ+sinnθsinθ

gn+1(cosθ)+gn−1(cosθ)=2cosnθcosθ=2cosθgn(cosθ)⇒gn+1(x)=2xgn(x)−gn−1(x)

我们就得到了切比雪夫多项式的递推公式。切比雪夫插值的代码如下：

两种曲线的拟合与预测

我们之前往往要求插值曲线严格的经过各个插值采样点，这个方式往往具有不可操控的地方。例如我们的采样点往往也只是一个粗略的估计，如果我们强行使插值曲线通过这些点，那么数据本身的误差也会反映在数据之中，例如下图中，使用一条直线去拟合获得的误差理论上要比经过这些点的曲线更加优秀。因此我们需要使用某种方式进行限制，这里我们介绍三种拟合方式。

直线拟合法

直线拟合是最为简单的拟合方法，也就是构造一套直线y=ax+b，使得我们的采样点近似的接近这条直线，我们有三种方式进行衡量拟合的优劣

准则一：使得误差最大绝对值最小
准则二：使得总误差的绝对值最小
准则三：使得误差平方和最小

其中准则三就是我们介绍的最小二乘法，我们就以准则三构造拟合的直线，那么设采样点有(xi,yi),i∈n，那么总误差为：

Min(Q)=∑i=1nei2=∑i=1n[yi−g(xi)]2=∑i=1n[yi−(axi+b)]2

容易发现我们的误差Q是关于a,b的函数，因此这里我们可以使用二元函数求导法则求得参数值。

∂Q∂a=−2∑i=1nxi(yi−axi−b)=0∂Q∂b=−2∑i=1n(yi−axi−b)=0⇒∑i=1nyi=a∑i=1nxi+nb∑i=1nxiyi=a∑i=1nxi2+b∑i=1nxi

联立上述式子可以解出a与b：

a=(∑i=1nxi2)(∑i=1nyi)−(∑i=1nxiyi)(∑i=1nxi)n∑i=1nxi2−(∑i=1nxi)2b=n(∑i=1nxiyi)−(∑i=1nxi)(∑i=1nyi)n∑i=1nxi2−(∑i=1nxi)2

采用直线拟合法，则需要保证采样点大致像直线的分布，或者说均匀分布在直线两侧，如果不符合这个则尽量不使用直线拟合。

对于某些增长型的曲线，我们可以采用指数函数y=aebx进行拟合，虽然是指数函数，我们可以将它化为直线方程，如下：

lny=lna+bx,Y=lny,B=b,lna=A⇒Y=A+BX

利用这个方程，我们可以利用直线拟合的手段，确定系数。不过检验我们的拟合精度的指标略微不同，指标为：

误差总平方和尽可能小
标准差σ=Q/(n+2)
相关系数R=1−∑(y~−yi)2∑(yi−y)2，R尽可能接近1

Reference

《数值分析》（原书第二版） —— Timothy Sauer

《数值计算方法》（清华大学出版社） —— 吕同富等

About Me

作　　者：WarrenRyan
出　　处：https://www.cnblogs.com/WarrenRyan/
本文对应视频：BiliBili
关于作者：热爱数学、热爱机器学习，喜欢弹钢琴的不知名小菜鸡。
版权声明：本文版权归作者所有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接。若需商用，则必须联系作者获得授权。
特此声明：所有评论和私信都会在第一时间回复。也欢迎园子的大大们指正错误，共同进步。或者直接私信我
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是作者坚持原创和持续写作的最大动力！

博主一些其他平台：
微信公众号：寤言不寐
BiBili——小陈的学习记录
Github——StevenEco
BiBili——记录学习的小陈（计算机考研纪实）
掘金——小陈的学习记录
知乎——小陈的学习记录

<a style="font-family: 微软雅黑; font-size: 18px;" href="mailto:[email protected]">电子邮件：[email protected] </a>
<br/>
<br/>

社交媒体联系二维码：

o_220106070541_%E4%B8%AA%E4%BA%BA%E4%BF%A1%E6%81%AF%E6%A0%8F.jpg

【机器学习】数值分析03——任意曲线拟合 - WarrenRyan

数值分析<3>——任意曲线拟合

万物皆是展开式

多项式插值法

拉格朗日插值法

一次线性插值

拉格朗日插值

*拉格朗日插值余项

Newton差商插值

牛顿差商公式

高次插值的Runge(龙格)现象

Hermite插值

Hermite插值余项

Chebyshev插值

两种曲线的拟合与预测

直线拟合法

Reference

About Me

Recommend

100多款高仿“羊了个羊”井喷，谁能复制日入百万造富神话？

9种常用UI界面中的控件规范，UI设计师要学的哦！

爆料大神猜测苹果10月或不办发布会，新iPad/Mac直接上线

C# 通用 HTTP 签名组件的另类实现 - [九零]

“网售处方药”开闸如何兼顾安全与便利？

打印 Logger 日志时，需不需要再封装一下工具类？

Your CTO Should Actually Be Technical

API composition

Learn How To Easily Keep All Your Project Documentation In Order

40 岁程序员会有哪些肺腑之言？这篇文章告诉你

About Joyk