Containers that support mapping isomorphic values.

This article series is part of a larger series of articles about functors, applicatives, and other mappable containers. So far, you've seen examples of both co- and contravariant functors, including profunctors. You've also seen a few examples of monomorphic functors - mappable containers where there's no variance at all.

What happens, on the other hand, if you have a container of (generic) values, but it's neither co- nor contravariant? An endomorphism is an example - it's neither co- nor contravariant. You'll see a treatment of that in a later article.

Even if neither co- nor contravariant mappings exists for a container, all may not be lost. It may still be an invariant functor.

Invariance #

Consider a container f (for functor). Depending on its variance, we call it covariant, contravariant, or invariant:

• Covariance means that any function a -> b can be lifted into a function f a -> f b.
• Contravariance means that any function a -> b can be lifted into a function f b -> f a.
• Invariance means that in general, no function a -> b can be lifted into a function over f a.

In general, that is. A limited escape hatch exists:

"an invariant type [...] allows you to map from a to b if and only if a and b are isomorphic. In a very real sense, this isn't an interesting property - an isomorphism between a and b means they're already the same thing to begin with."

Sandy Maguire, Thinking with Types

In Haskell we may define an invariant functor (AKA exponential functor) as in the invariant package:

class Invariant f where
  invmap :: (a -> b) -> (b -> a) -> f a -> f b

This means that an invariant functor f is a container of values where a translation from f a to f b exists if it's possible to translate contained values both ways: From a to b, and from b to a. Callers of the invmap function must supply translations that go both ways.

Invariant functor in C# #

It's possible to translate the concept to a language like C#. Since C# doesn't have higher-kinded types, we have to examine the abstraction as a set of patterns or templates. For functors and monads, the C# compiler can perform 'compile-time duck typing' to recognise these motifs to enable query syntax. For more advanced or exotic universal abstractions, such as bifunctors, profunctors, or invariant functors, we have to use a concrete container type as a stand-in for 'any' functor. In this article, I'll call it Invariant<A>.

Such a generic class must have a mapping function that corresponds to the above invmap. In C# it has this signature:

public Invariant<B> InvMap<B>(Func<A, B> aToB, Func<B, A> bToA)

In this example, InvMap is an instance method on Invariant<A>. You may use it like this:

Invariant<long> il = createInvariant();
Invariant<TimeSpan> its = il.InvMap(l => new TimeSpan(l), ts => ts.Ticks);

It's not that easy to find good examples of truly isomorphic primitives, but TimeSpan is just a useful wrapper of long, so it's possible to translate back and forth without loss of information. To create a TimeSpan from a long, you can use the suitable constructor overload. To get a long from a TimeSpan, you can read the Ticks property.

Perhaps you find a method name like InvMap non-idiomatic in C#. Perhaps a more idiomatic name might be Select? That's not a problem:

public Invariant<B> Select<B>(Func<A, B> aToB, Func<B, A> bToA)
{
    return InvMap(aToB, bToA);
}

In that case, usage would look like this:

Invariant<long> il = createInvariant();
Invariant<TimeSpan> its = il.Select(l => new TimeSpan(l), ts => ts.Ticks);

In this article, I'll use Select in order to be consistent with C# naming conventions. Using that name, however, will not make query syntax light up. While the name is fine, the signature is not one that the C# compiler will recognise as enabling special syntax. The name does, however, suggest a kinship with a normal functor, where the mapping in C# is called Select.

Laws #

As is usual with these kinds of universal abstractions, an invariant functor must satisfy a few laws.

The first one we might call the identity law:

invmap id id = id

This law corresponds to the first functor law. When performing the mapping operation, if the values in the invariant functor are mapped to themselves, the result will be an unmodified functor.

In C# such a mapping might look like this:

var actual = i.Select(x => x, x => x);

The law then says that actual should be equal to i.

The second law we might call the composition law:

invmap f2 f2' . invmap f1 f1' = invmap (f2 . f1) (f1' . f2')

Granted, this looks more complicated, but also directly corresponds to the second functor law. If two sequential mapping operations are performed one after the other, the result should be the same as a single mapping operation where the functions are composed.

In C# the left-hand side might look like this:

Invariant<IntPtr> left = i.Select(f1, f1p).Select(f2, f2p);

In C# you can't name functions or variables with a quotation mark (like the Haskell code's f1' and f2'), so instead I named them f1p and f2p (with a p for prime).

Likewise, the right-hand side might look like this:

Invariant<IntPtr> right = i.Select(ts => f2(f1(ts)), ip => f1p(f2p(ip)));

The composition law says that the left and right values must be equal.

You'll see some more detailed examples in later articles.

Examples #

This is all too abstract to seem useful in itself, so example are warranted. You'll be able to peruse examples of specific invariant functors in separate articles:

• Endomorphism as an invariant functor
• Natural transformations as invariant functors
• Functors as invariant functors
• Contravariant functors as invariant functors

As two of the titles suggest, all functors are also invariant functors, and the same goes for contravariant functors:

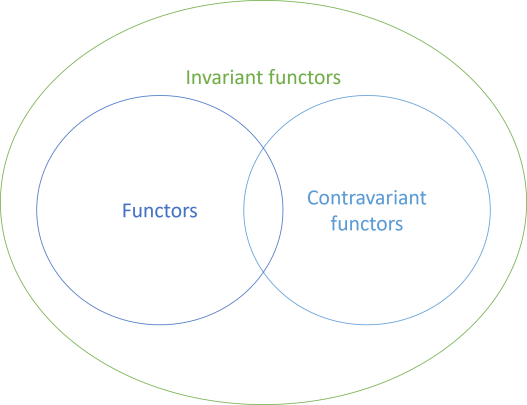
To be honest, invariant functors are exotic, and you are unlikely to need them in all but the rarest cases. Still, I did run into a scenario where I needed an invariant functor instance to be able to perform a particular sleight of hand. The rabbit holes we sometimes fall into...

Conclusion #

Invariant functors form a set that contains both co- and contravariant functors, as well as some data structures that are neither. This is an exotic abstraction that you may never need. It did, however, get me out of a bind at one time.

Next: Endomorphism as an invariant functor.