从傅里叶级数（Fourier series）到离散傅里叶变换（Discrete Fourier transform） - M...

从傅里叶级数（Fourier series）到离散傅里叶变换（Discrete Fourier transform）

一. 傅里叶级数（FS）

首先从最直观的开始，我们有一个信号x(t)（满足Dirichelet条件），先假设它是周期的，为了研究它，我们使用级数将之展开，展开方法如下

现在问题就是如何求解ak。因为三角函数是正交系，即

这样我们就可以进行如下操作：

对（1）式左右同时积分：

故（3）积分的结果如下：

于是我们得到了ak：

这样我们就把一个周期信号分解成了一系列模为ak的复周期信号的组合，形象表示就是这样：

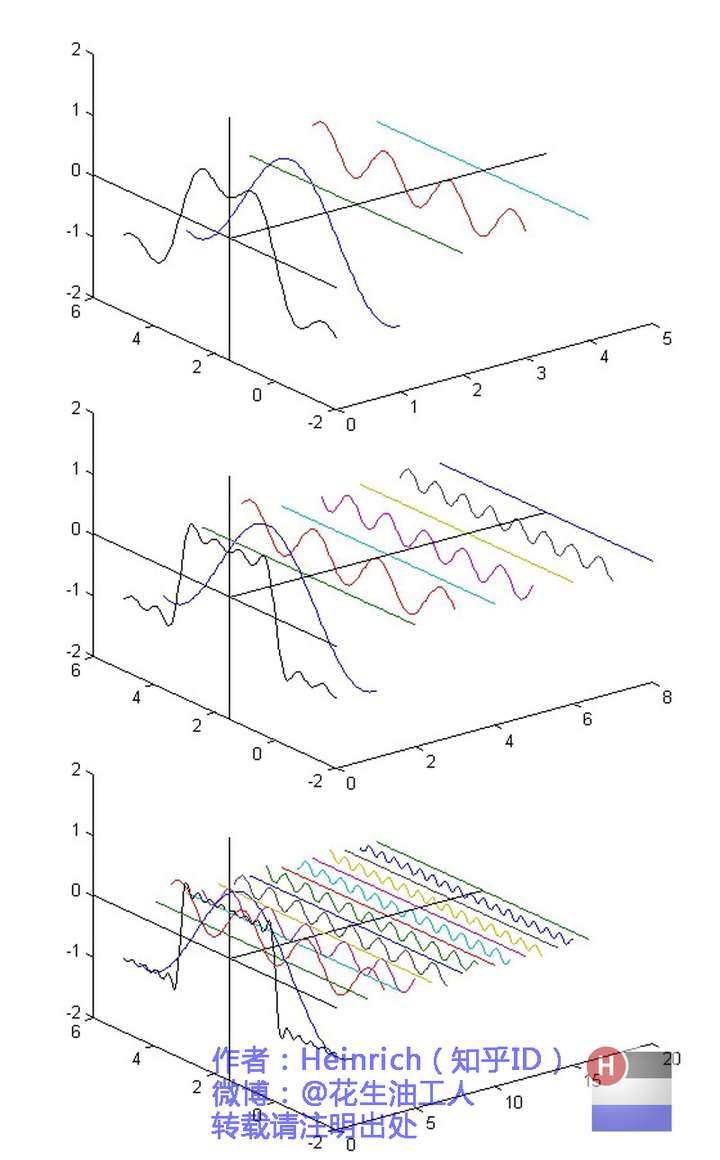
图片来源：傅里叶分析之掐死傅里叶教程https://zhuanlan.zhihu.com/p/19763358（推荐大家看看）

OK，到这里我们成功将一个周期信号分解成了傅里叶级数。但是这里也有两个问题依然困扰着我：

1.首先（相信大家也注意到了我第一句标黄的内容），非周期有限信号能不能展开成傅里叶级数呢？

比如，如果有一个函数，它是这样的：

我们同样可以在0-T上做积分，并且得到s(t)的ak和x(t)的ak是相同的，也就是说，可以把s(t)写成：

但是咱也理解，这样的一个式子大概率不能叫做级数，充其量叫个级数的一部分。不过我们主要研究信号，就不关心这些数学概念了。那么对于这样的一个信号，傅里叶级数还能不能表达它的频谱特性呢？它的频谱跟x(t)又有什么联系呢？,这两个问题我们在第二部分解答。

2. 三角函数系的正交性强调的是一个周期内的积分，但是没有说一定是最小正周期，如果我们在2T、3T或者nT上积分，会发生什么呢？

回答这个问题之前，我们先对傅里叶级数做一个比较统筹的显示，我们不妨以w作为横坐标，以akejkw0的强度（也就是||akejkw0||=|ak|）作为纵坐标，构建一个二维直角坐标系(数据大小是随便给的)：

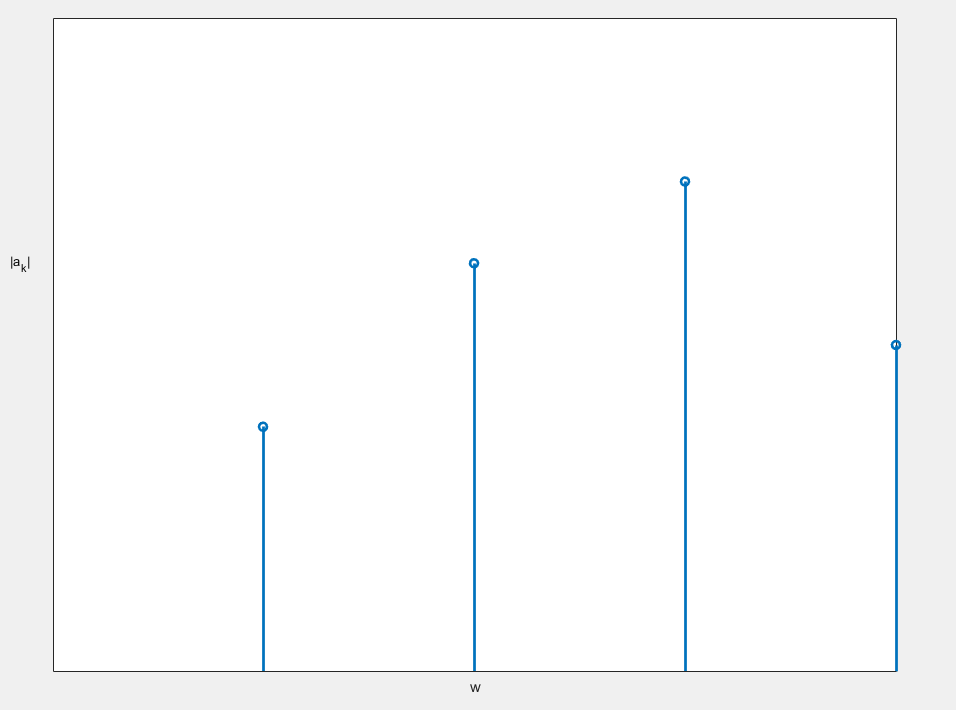
分析这个图，我们知道每两个”柱子“之间的距离应该是Δw=w0=2πT，所以，如果我们增大T，两个数据之间的距离就会变小，如下：

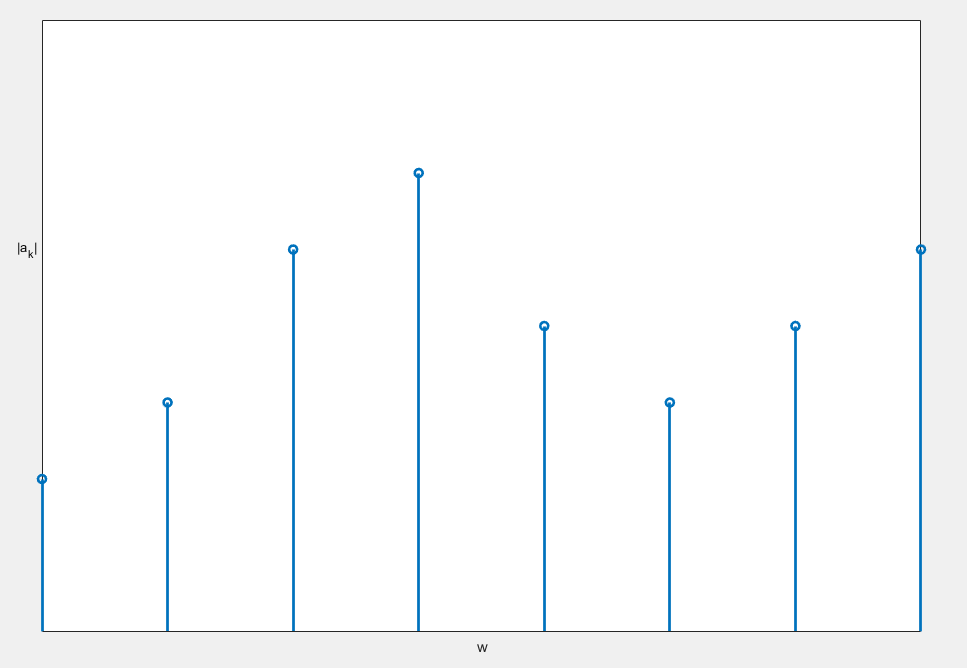
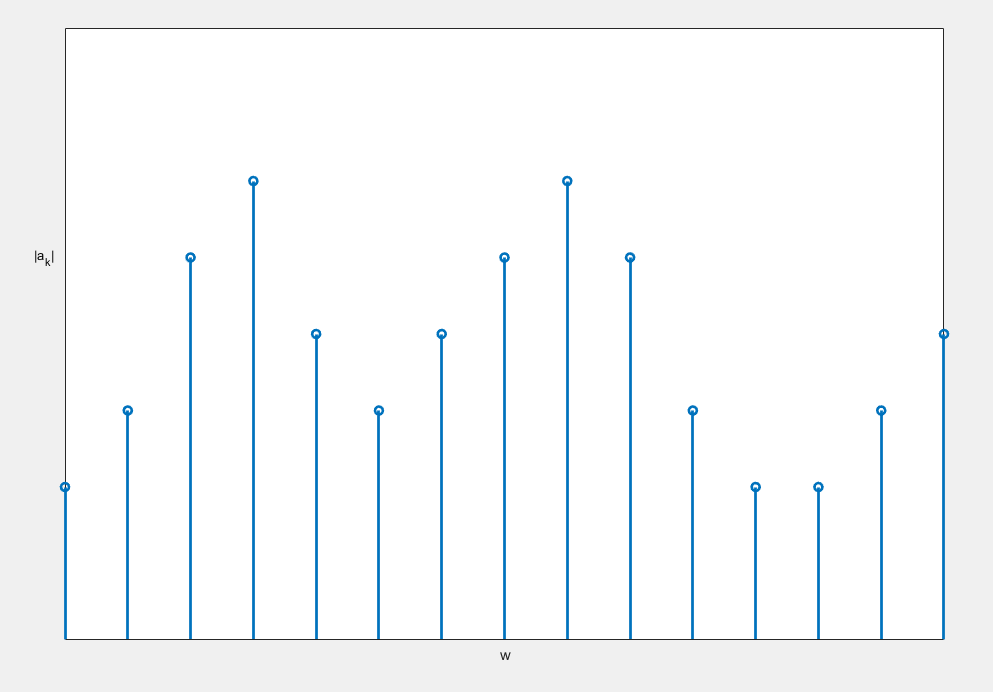
可以看到，T越大,两个数据之间的横轴距离就越小，不妨做个猜想：当T→∞时，这个离散的谱就变成了连续谱。是这样吗？应该说对有限信号是这样的，对无限周期信号则不是，这是为什么呢？请看下一节傅里叶变换的解读。

二. 傅里叶变换（FT）

2.1 傅里叶变换的推导

接着前面的猜想进行分析，为了得到可靠结论，我们进行如下数学分析：

接着（5）式开展：

用w0=2πT替代T，同时将x(t)表示出来:

当w0→0时，可用w0=dw表示它，此外，对于kw0的累加就变成了积分（累加步长kw0无限小）,故而上式变成了：

这样我们实现了将一个信号分解成连续的频谱，而这个频谱就是：

（6）式就是傅里叶变换的基本形式，当然有些地方可能将系数12π进行了一些变换,比如：

这些都是小细节，咱们就不在意了。

2.2 周期函数的傅里叶变换

观察（8）这个式子，我们很快又发现了另外一个问题，积分区域是无穷，而周期函数在无穷区间积分，那必然是发散的，怎么解呢？

我们是这样处理的：

1. 首先将x(t)表示成傅里叶级数：

   x(t)=∑kakejkwot

2. 对级数做傅里叶变换，也就是：

   X(w)=∑kF(akejkwot)=ak∑kF(ejkw0t)

​ 于是问题转化成了如何求ejkw0t的傅里叶变换，这个就要使用傅里叶变换的基本性质了：信号乘以ejw0t相当于傅里叶变换X(w)进行频移w0， 这个我们也可以顺便证明一下：

​ 又由于：

​ 把（10）代入（9），就得到了周期函数的傅里叶变换：

可以看出，周期函数的傅里叶变换是一系列冲击串，这个倒也符合我们的直觉：

傅里叶变换每个X(w)可以理解为信号频率为w的分量的大小，对于周期信号，它的每一个频率分量都是一个无限长信号，所以每一个分量的能量都是无穷的，所以在频谱上就表示为冲击串了。

2.3 有限长非周期信号的傅里叶变换

好了，现在我们来解答第一节中的第二个问题：有限长非周期信号的傅里叶变换和周期信号频谱的关系。

对于有限长信号：

可以换一种表达方式:

要求F[s(t)]，我们首先需要以下几个结论：

1. 时域相乘等于频域卷积，证明:

   若Z(w)=X(w)∗Y(w),则z(t)=F−1(Z(w))=∫∞[∫∞X(m)Y(w−m)dm]ejwtdt=∫∞X(m)[∫∞Y(w−m)ejwtdt]dm=∫∞X(m)y(t)ejmtdm=x(t)y(t)得证

   注：如果从采用z(t)=x(t)y(t)出发，去证明Z(w)=X(w)∗Y(w)会比较麻烦。

2. F[u(t)−u(t−T)]=1−e−jwtjw，这个就很好证明了:

   F[u(t)−u(t−T)]=∫T0x(t)e−jwtdt=1−e−jwtjw

   这个函数展现的频谱图像如下：

   

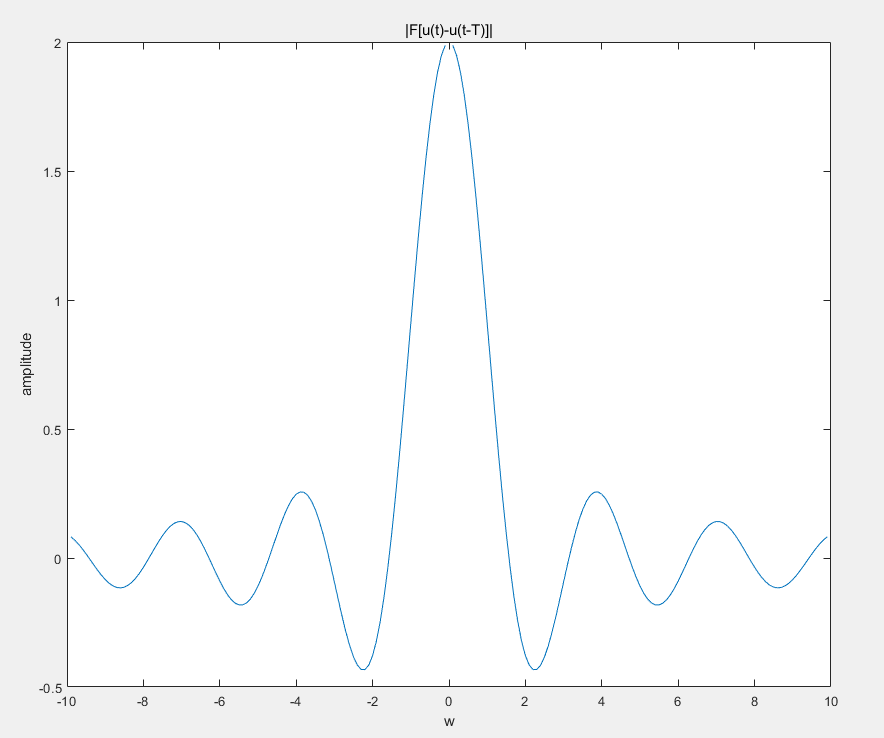
好了，我们现在可以开始计算（6）式s(t)的傅里叶变换了：

及∑kδ(w−kw0)∗1−e−jwtjw就是F[u(t)−u(t−T)]以kw0移位叠加,一些一组图表示这个过程：

简单起见，我们令|X(w)|为：

对它进行卷积，也就是将下面两个信号叠加：

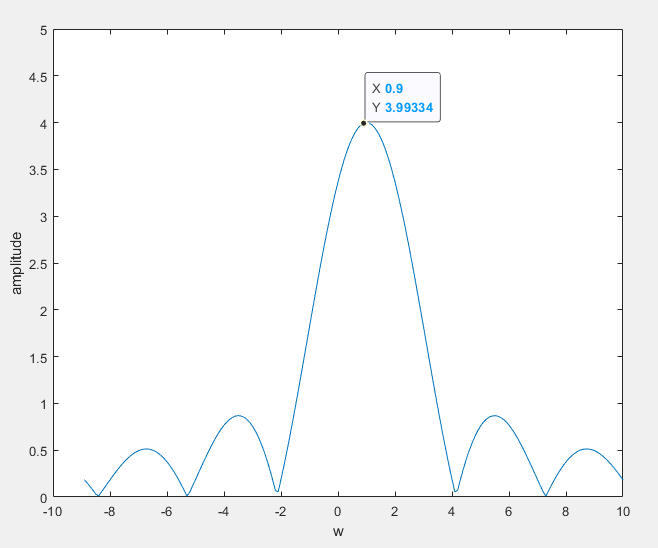
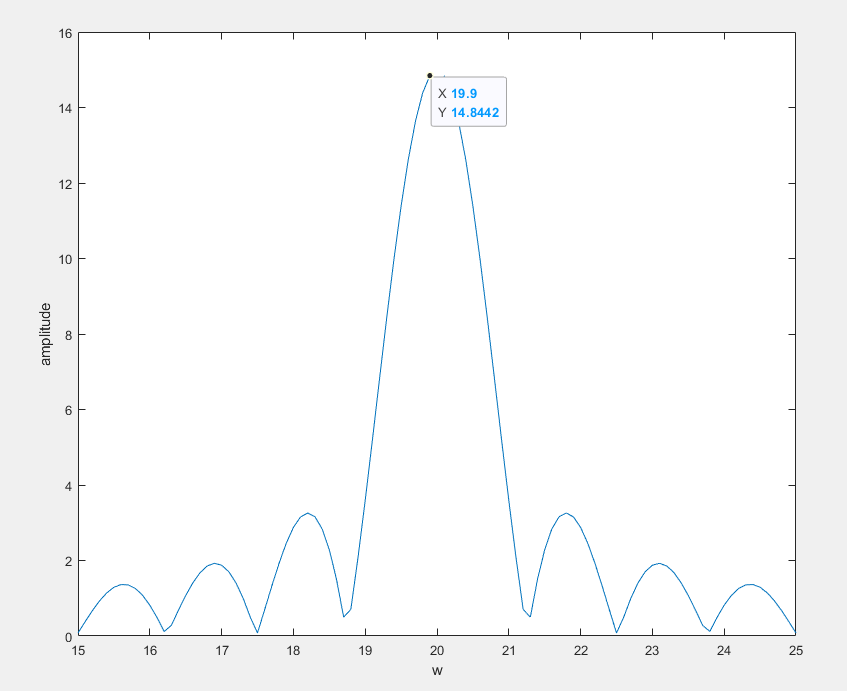
于是得到|S(w)|：

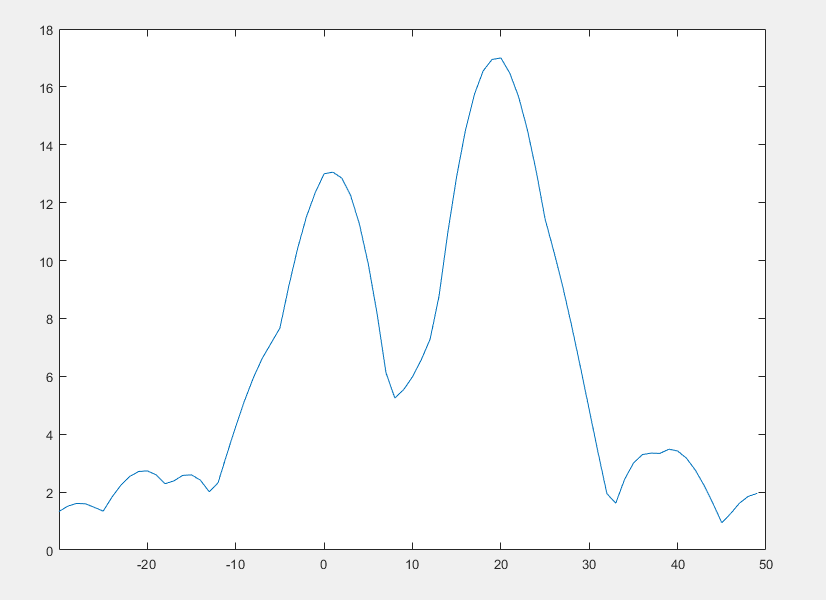
图不咋好看，可能是频率分辨率没调好，但是大概样子大家能看清楚了，也就是在周期信号的频谱里的冲击串变得平滑了，或者换句话说，原来集中在某个kw0频率的能量一部分泄露到了全频域。

这个在物理意义上也比较好理解，把周期信号截断了，实际上是把一部分信号值变成了0，从某个值突然变到0(x(T)->0)，这里没有平滑过渡，是一个突变，而我们知道，突变包含所有频率分量。

至此，我们完成了傅里叶级数到傅里叶变换的推导。

三、时域离散化

在实际应用中，我们大多处理的是数字信号，也就是时域离散的信号，我们来看看时域离散对信号频谱的影响。

这个时候，我们可以把信号表示为

根据（10），利用傅里叶变换的对偶性，可以得出：

所以x(t)的傅里叶变换为：

也就是说，x(n)的傅里叶变换就是下x(t)的傅里叶变换以ws为周期，移位叠加。

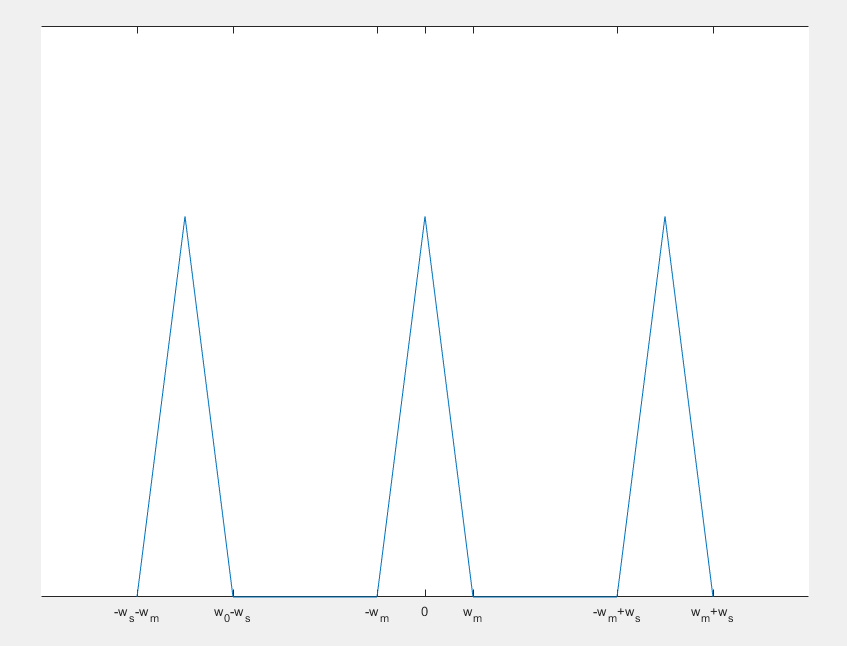
如上图，假设中间的三角形就是X(w)，则它经过移位叠加后得到的上图就是F(x(n))。

从这张图我们也可以看出一个重要的定理——奈奎斯特采样定理：采样频率需要高于信号最高频率的两倍，因为如果不能满足

就会发生频谱混叠（上图的两个相邻三角形叠在一起了）。

这样我们就得到了时域离散信号的傅里叶变换，但是显然，这样得到的频谱也是连续的，计算机存储的是离散信号，那么如何将频域也离散化呢？请看下节。

四、DFT

回顾前面的内容，我们发现，满足频域离散的只有一种信号，那就是周期信号。于是让信号离散化的方法就呼之欲出了：

假设我们采集到的N个数据其实是一个周期信号的一个周期，或者换句话说，我们把这N点数据以N为周期进行延拓，那么接下来要做的就是对一个周期信号的傅里叶变换了，又时域是离散的，傅里叶变换就退化成了傅里叶级数形式：

现在好了，时域和频域都是离散的了，而且频域和时域一样只有N个点。并且通过上面时域离散造成频域以采样角频率ws拓展的结论，我们可以知道，这个数字频谱，其实就是在长度为ws的区间内插入了N个点，所以没两个点之间的频率间隔为

这个Δw也叫做频率分辨率，也就是通过这个频谱能区分的两个频率最小的间隔。

这里我们再对模拟角频率Ω和数字角频率做一个区分：

在模拟域，频率f表示的是一个信号每秒重复变化的次数，模拟角频率Ω=2πf表示的就是单位时间内信号相位角变换的弧度。可以把一个重复的信号想象成一个点做圆周运动，f表示它单位时间绕了多少圈，w表示它单位时间转过多少弧度。

在数字域，我们同样可以通过单位时间信号相位角的该变量来表示角频率，但是数字域只有单位1，无连续时间的概念，长度为N的序列，两个点相隔的时间是1fs，所以数字域的“时间”每改变1，角度改变应该是：

上式还可以写作w=2πffs，又由采样定理知fs>2f,所以w<π，但是我们常常取数字频域的0−fs进行研究，也就是说w最大取到2π(实际上是0移位一个周期得到的)，可见：w被限制在了[0 2π]，所以我们也称数字角频率w为归一化频率。

---

其实上述所有的推导都能在《信号与系统》和《数字信号处理》教材里找到，我只是做了一个整理和总结，建议大家还是精读课本，写书的人一般比写博客的人强。