如何判定完美矩形

通知： 持续更新中， 开始报名， 开始预约。

读完本文，你不仅学会了算法套路，还可以顺便解决如下题目：

牛客	LeetCode	力扣	难度
-			🔴

———–

今天讲一道非常有意思，而且比较有难度的题目。

我们知道一个矩形有四个顶点，但是只要两个顶点的坐标就可以确定一个矩形了（比如左下角和右上角两个顶点坐标）。

今天来看看力扣第 391 题「

」，题目会给我们输入一个数组 rectangles，里面装着若干四元组 (x1,y1,x2,y2)，每个四元组就是记录一个矩形的左下角和右上角坐标。

也就是说，输入的 rectangles 数组实际上就是很多小矩形，题目要求我们输出一个布尔值，判断这些小矩形能否构成一个「完美矩形」。函数签名如下：

def isRectangleCover(rectangles: List[List[int]]) -> bool

所谓「完美矩形」，就是说 rectangles 中的小矩形拼成图形必须是一个大矩形，且大矩形中不能有重叠和空缺。

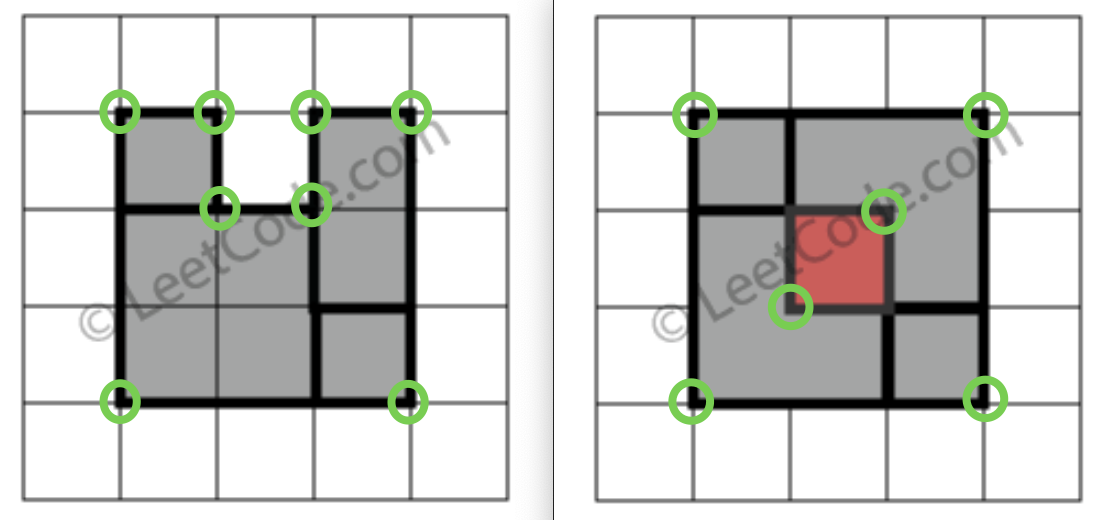
比如说题目给我们举了几个例子：

这个题目难度是 Hard，如果没有做过类似的题目，还真做不出来。

常规的思路，起码要把最终形成的图形表示出来吧，而且你要有方法去判断两个矩形是否有重叠，是否有空隙，虽然可以做到，不过感觉异常复杂。

其实，想判断最终形成的图形是否是完美矩形，需要从「面积」和「顶点」两个角度来处理。

先说说什么叫从「面积」的角度。

rectangles 数组中每个元素都是一个四元组 (x1, y1, x2, y2)，表示一个小矩形的左下角顶点坐标和右上角顶点坐标。

那么假设这些小矩形最终形成了一个「完美矩形」，你会不会求这个完美矩形的左下角顶点坐标 (X1, Y1) 和右上角顶点的坐标 (X2, Y2)？

这个很简单吧，左下角顶点 (X1, Y1) 就是 rectangles 中所有小矩形中最靠左下角的那个小矩形的左下角顶点；右上角顶点 (X2, Y2) 就是所有小矩形中最靠右上角的那个小矩形的右上角顶点。

注意我们用小写字母表示小矩形的坐标，大写字母表示最终形成的完美矩形的坐标，可以这样写代码：

# 左下角顶点，初始化为正无穷，以便记录最小值
X1, Y1 = float('inf'), float('inf')
# 右上角顶点，初始化为负无穷，以便记录最大值
X2, Y2 = -float('inf'), -float('inf')

for x1, y1, x2, y2 in rectangles:
    # 取小矩形左下角顶点的最小值
    X1, Y1 = min(X1, x1), min(Y1, y1)
    # 取小矩形右上角顶点的最大值
    X2, Y2 = max(X2, x2), max(Y2, y2)

这样就能求出完美矩形的左下角顶点坐标 (X1, Y1) 和右上角顶点的坐标 (X2, Y2) 了。

计算出的 X1,Y1,X2,Y2 坐标是完美矩形的「理论坐标」，如果所有小矩形的面积之和不等于这个完美矩形的理论面积，那么说明最终形成的图形肯定存在空缺或者重叠，肯定不是完美矩形。

代码可以进一步：

def isRectangleCover(rectangles: List[List[int]]) -> bool:
    X1, Y1 = float('inf'), float('inf')
    X2, Y2 = -float('inf'), -float('inf')
    # 记录所有小矩形的面积之和
    actual_area = 0
    for x1, y1, x2, y2 in rectangles:
        # 计算完美矩形的理论坐标
        X1, Y1 = min(X1, x1), min(Y1, y1)
        X2, Y2 = max(X2, x2), max(Y2, y2)
        # 累加所有小矩形的面积
        actual_area += (x2 - x1) * (y2 - y1)

    # 计算完美矩形的理论面积
    expected_area = (X2 - X1) * (Y2 - Y1)
    # 面积应该相同
    if actual_area != expected_area:
        return False

    return True

这样，「面积」这个维度就完成了，思路其实不难，无非就是假设最终形成的图形是个完美矩形，然后比较面积是否相等，如果不相等的话说明最终形成的图形一定存在空缺或者重叠部分，不是完美矩形。

但是反过来说，如果面积相同，是否可以证明最终形成的图形是完美矩形，一定不存在空缺或者重叠？

肯定是不行的，举个很简单的例子，你假想一个完美矩形，然后我在它中间挖掉一个小矩形，把这个小矩形向下平移一个单位。这样小矩形的面积之和没变，但是原来的完美矩形中就空缺了一部分，也重叠了一部分，已经不是完美矩形了。

综上，即便面积相同，并不能完全保证不存在空缺或者重叠，所以我们需要从「顶点」的维度来辅助判断。

记得小学的时候有一道智力题，给你一个矩形，切一刀，剩下的图形有几个顶点？答案是，如果沿着对角线切，就剩 3 个顶点；如果横着或者竖着切，剩 4 个顶点；如果只切掉一个小角，那么会出现 5 个顶点。

回到这道题，我们接下来的分析也有那么一点智力题的味道。

显然，完美矩形一定只有四个顶点。矩形嘛，按理说应该有四个顶点，如果存在空缺或者重叠的话，肯定不是四个顶点，比如说题目的这两个例子就有不止 4 个顶点：

PS：我也不知道应该用「顶点」还是「角」来形容，好像都不太准确，本文统一用「顶点」来形容，大家理解就好~

只要我们想办法计算 rectangles 中的小矩形最终形成的图形有几个顶点，就能判断最终的图形是不是一个完美矩形了。

那么顶点是如何形成的呢？我们倒是一眼就可以看出来顶点在哪里，问题是如何让计算机，让算法知道某一个点是不是顶点呢？这也是本题的难点所在。

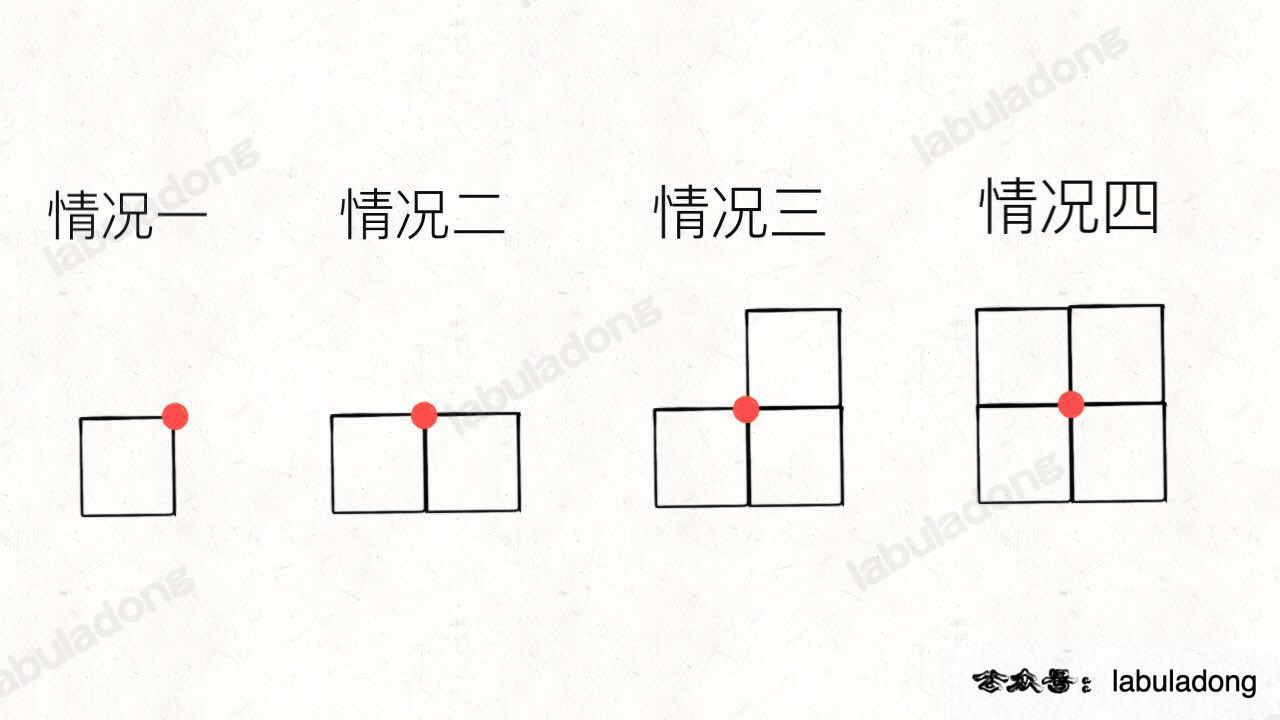
看下图的四种情况：

图中画红点的地方，什么时候是顶点，什么时候不是顶点？显然，情况一和情况三的时候是顶点，而情况二和情况四的时候不是顶点。

也就是说，当某一个点同时是 2 个或者 4 个小矩形的顶点时，该点最终不是顶点；当某一个点同时是 1 个或者 3 个小矩形的顶点时，该点最终是一个顶点。

注意，2 和 4 都是偶数，1 和 3 都是奇数，我们想计算最终形成的图形中有几个顶点，也就是要筛选出那些出现了奇数次的顶点，可以这样写代码：

def isRectangleCover(rectangles: List[List[int]]) -> bool:
    X1, Y1 = float('inf'), float('inf')
    X2, Y2 = -float('inf'), -float('inf')

    actual_area = 0
    # 哈希集合，记录最终图形的顶点
    points = set()
    for x1, y1, x2, y2 in rectangles:
        X1, Y1 = min(X1, x1), min(Y1, y1)
        X2, Y2 = max(X2, x2), max(Y2, y2)

        actual_area += (x2 - x1) * (y2 - y1)
        # 先算出小矩形每个点的坐标
        p1, p2 = (x1, y1), (x1, y2)
        p3, p4 = (x2, y1), (x2, y2)
        # 对于每个点，如果存在集合中，删除它；
        # 如果不存在集合中，添加它；
        # 在集合中剩下的点都是出现奇数次的点
        for p in [p1, p2, p3, p4]:
            if p in points: points.remove(p)
            else: points.add(p)

    expected_area = (X2 - X1) * (Y2 - Y1)
    if actual_area != expected_area:
        return False

    return True

这段代码中，我们用一个 points 集合记录 rectangles 中小矩形组成的最终图形的顶点坐标，关键逻辑在于如何向 points 中添加坐标：

如果某一个顶点 p 存在于集合 points 中，则将它删除；如果不存在于集合 points 中，则将它插入。

这个简单的逻辑，让 points 集合最终只会留下那些出现了 1 次或者 3 次的顶点，那些出现了 2 次或者 4 次的顶点都被消掉了。

那么首先想到，points 集合中最后应该只有 4 个顶点对吧，如果 len(points) != 4 说明最终构成的图形肯定不是完美矩形。

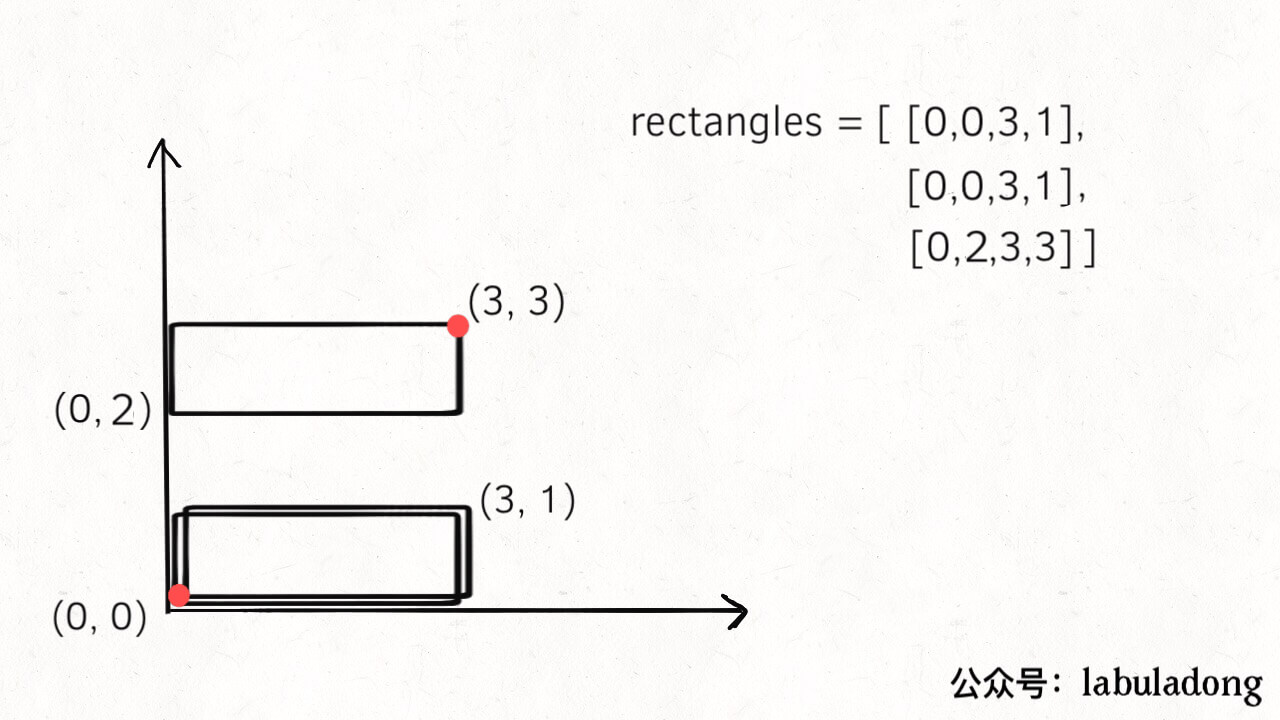
但是如果 len(points) == 4 是否能说明最终构成的图形肯定是完美矩形呢？也不行，因为题目并没有说 rectangles 中的小矩形不存在重复，比如下面这种情况：

下面两个矩形重复了，按照我们的算法逻辑，它们的顶点都被消掉了，最终是剩下了四个顶点；再看面积，完美矩形的理论坐标是图中红色的点，计算出的理论面积和实际面积也相同。但是显然这种情况不是题目要求完美矩形。

所以不仅要保证 len(points) == 4，而且要保证 points 中最终剩下的点坐标就是完美矩形的四个理论坐标，直接看代码吧：

def isRectangleCover(rectangles: List[List[int]]) -> bool:
    X1, Y1 = float('inf'), float('inf')
    X2, Y2 = -float('inf'), -float('inf')
    
    points = set()
    actual_area = 0
    for x1, y1, x2, y2 in rectangles:
        # 计算完美矩形的理论顶点坐标
        X1, Y1 = min(X1, x1), min(Y1, y1)
        X2, Y2 = max(X2, x2), max(Y2, y2)
        # 累加小矩形的面积
        actual_area += (x2 - x1) * (y2 - y1)
        # 记录最终形成的图形中的顶点
        p1, p2 = (x1, y1), (x1, y2)
        p3, p4 = (x2, y1), (x2, y2)
        for p in [p1, p2, p3, p4]:
            if p in points: points.remove(p)
            else:           points.add(p)
    # 判断面积是否相同
    expected_area = (X2 - X1) * (Y2 - Y1)
    if actual_area != expected_area:
        return False
    # 判断最终留下的顶点个数是否为 4
    if len(points) != 4:       return False
    # 判断留下的 4 个顶点是否是完美矩形的顶点
    if (X1, Y1) not in points: return False
    if (X1, Y2) not in points: return False
    if (X2, Y1) not in points: return False
    if (X2, Y2) not in points: return False
    # 面积和顶点都对应，说明矩形符合题意
    return True

这就是最终的解法代码，从「面积」和「顶点」两个维度来判断：

1、判断面积，通过完美矩形的理论坐标计算出一个理论面积，然后和 rectangles 中小矩形的实际面积和做对比。

2、判断顶点，points 集合中应该只剩下 4 个顶点且剩下的顶点必须都是完美矩形的理论顶点。

＿＿＿＿＿＿＿＿＿＿＿＿＿

《labuladong 的算法小抄》已经出版，关注公众号查看详情；后台回复关键词「进群」可加入算法群；回复「PDF」可获取精华文章 PDF：