1

CNN Meets Graphs

 2 years ago
source link: https://sighingnow.github.io/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/cnn_meets_graph.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
neoserver,ios ssh client

CNN Meets Graphs

May 16, 2017 • Tao He| GCN, Graph Theory, 机器学习

Graph convolutional network is a kind of neural network that use graph data as input, developing a serials of Conv operator and Pooling theory based on graph theory, mainly the spectral graph theory.

Spectral Graph Theory

对于无向图G的链接矩阵A，按如下方式定义度矩阵D（D是一个对角阵）

Dii=∑jAij

在此基础上定义图的Laplacian矩阵

L=D−A

L是一个实对称矩阵，因此L必然可以对角化，可以分解为L=UΛU−1的形式， 其中Λ是L的特征值组成的对角阵，U是L的特征向量矩阵，并且U是一个单位正交 矩阵，有UT=U−1。因此，L分解可以进一步表达为

L=UΛU−1=UΛUT

对 Laplacian 矩阵进行正规化，得到

L=I−D−1/2AD−1/2

Spectral and Convolution

符号约定：

  • f，g，h是一维或二维连续函数
  • x，m，n，i，j是自变量
  • ⋆ 表示卷积算符，⋅表示普通的乘法算符，⊙表示两个向量之间的ElementWise乘积
  • F表示离散傅里叶变换或连续傅里叶变换，F−1表示相应的傅里叶逆变换

卷积的定义

一维连续卷积的定义，若h是f和g的卷积，即h=f∗g，那么

h(x)=∫−∞∞f(t)⋅g(x−t)dt

二维连续卷积的定义，若h是f和g的卷积，即h=f∗g，那么

h(i,j)=∫∞infty∫∞∞f(m,n)⋅g(i−m,j−n)dmdn

接下来考虑有限尺度上的二维离散卷积，例如图片上的卷积，假定 f 表示二维图像，g 表示卷积核（尺度小于f），仍然有h=f∗g，那么

h(i,j)=∑m=−MM∑n=−NNf(m,n)⋅g(i−m,j−n)

其中，，M=⌊R(g)/2⌋，N=⌊C(g)/2⌋。

卷积定理：函数卷积的傅里叶变换是函数傅里叶变换的乘积，即一个域中的卷积对应于 另一个域的乘积，因此，时（空）域上的卷积运算可以转换为其在频域上的乘积，在对结果 做傅里叶逆变换，

f∗g=F−1{F{f}⋅F{g}}

Laplacian矩阵与傅里叶变换

拉普拉斯算子是欧式空间上的一个二维微分算子，定义为

Δf=∑i=1n∂2f∂xi2

因此，Laplacian矩阵的特征矩阵可以作为傅里叶变换的基，即 ${\mathcal{F}{f} = U^T f$。

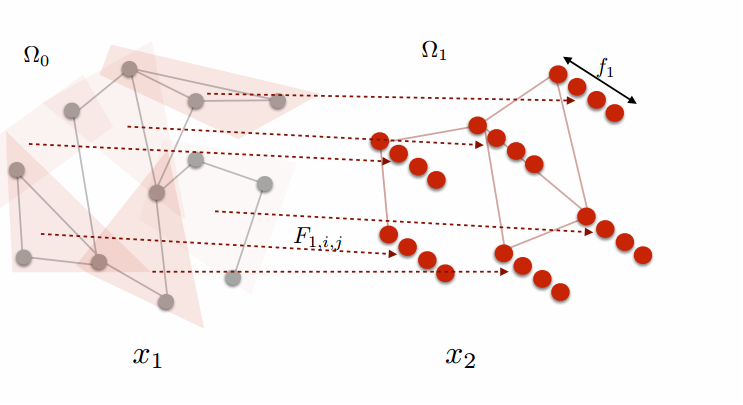
考虑向量f, g，不妨假定f代表图上的点，g代表卷积核，则卷积操作

f∗g=F−1(Ff⊙Fg)=U((UTf)⊙(UTg))=U((UTg)⊙(UTf))=U(g^⊙(UTf))=Udiag(g^)UTf

将diag(g^)的对角线上的n个元素g^i分别视为L的n个特征值λi 的函数，那么，下列公式中的卷积可以表达为

f∗g=Udiag(g^)UTf=U[g^(λ1)⋱g^(λn)]UTf=Ug^(Λ)UFf

其中，g^i是需要训练的参数，规模为O(n)，并且，对于每个卷积层，都需要预先计算好Laplacian矩阵 的特征向量矩阵。

多项式近似

根据1中的结论，g^(Λ)可以有在K阶Chebyshev多项式上的有限项展开近似，

g^(Λ)≈∑k=0KθkTk(Λ~)

其中，Λ~=2λmaxΛ−IN，λmax表示L的最大 的特征值（实际实验中近似处理为223，省去求Laplacian矩阵最大特征值的计算步骤）。Chebyshev多 项式的递归定义为

Tk(x)=2xTk−1(x)−Tk−2(x)

其中，T0(x)=1，T1(x)=x。

假定对于非负整数k，h=θkxk，不难得出关于h(Λ)的等式

Uh(Λ)UT=UθkΛkUT=θk(UΛUT)k=θkLk

也就意味着Λ的多项式可以转换为L的多项式，约等式中g^(Λ)的近似 多项式展开可以表示为

g^(Λ)≈∑k=0KθkTk(Λ~)=∑k=0KθkTk(L~)

其中，L~=2λmaxL−IN。此时Laplacian矩阵的K阶多项式包含了K近邻的含义2， θk为需要训练的参数，规模为O(K)，为常数复杂度。

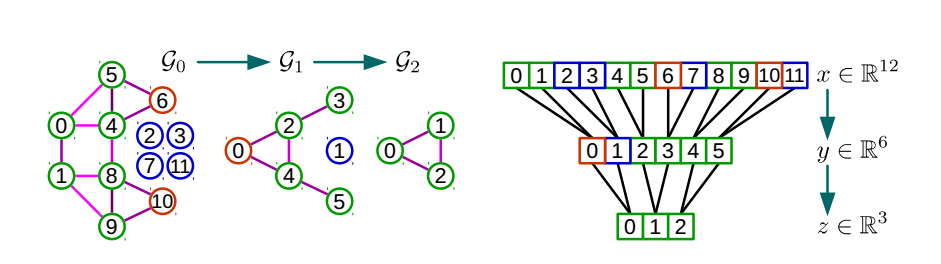
对于一个图，通过点与点之间的近邻信息可以对图进行聚类，将每个类用一个新的点表示，得到图的粗化结果。 位于不同类的两个点之间有连接关系，则对聚类结果中代表这两个类的新点之间建立连接关系。

  1. 下图是4中提到的多层级聚类方法。

    Hierarchical Clustering of Graph

  2. 下图是5中提到的每次使图的大小减小一般的粗化方法。

    Graph Coarsening and Pooling

  • 输入：图的邻接矩阵A及每个点的特征Fij0
  • 输出：图的特征

图的粗化与多层CNN

对于多层CNN模型，每一个卷积层都会用到该层输入的图的Laplacian矩阵，需要对原始图进行预处理，对每个 池化层，都根据池化层输入输出的规模对图做一次粗化。在预处理数据阶段，要根据设计好的神经网络的结构， 按照每一层的大小对图进行粗化处理，算出每一次粗化处理得到的图的Laplacian矩阵。之后做池化操作时， 使用粗化时预先计算好的近邻关系，做卷积操作时，使用粗化时预先计算好的Laplacian矩阵。

模型的改进

图片采样为图

  • 输入：图片
  • 输出：图的邻接矩阵A、每个点的特征 Fij0

高阶模式的应用

  • 输入：基本图案（Motif）、图的邻接矩阵A、每个点的特征Fij0
  • 输出：新的图的邻接矩阵A′、每个点的特征F‘ij0

Higher Order Originazation

论文6通过利用一个图的某种特定模式的图案（Motif）定义了新的RatioCut

ϕM(S)=cutM(S,S¯)min[volM(S),volM(S¯]

并且从理论上证明了新定义的RatioCut仍然满足Cheeger不等式7：

ϕM(S)≤4ϕM∗

其中，ϕM(S)是实际求得的最优解，ϕM∗是理论最优解。

References

  1. Wavelets on Graphs via Spectral Graph Theory ↩

  2. Semi-supervised Classification with Graph Convolutional Networks[iclr2017] ↩ ↩2

  3. https://github.com/mdeff/cnn_graph/blob/master/lib/graph.py#L232 ↩

  4. Spectral Networks and Locally Connected Networks on Graphs[iclr2014] ↩

  5. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering[nips2016] ↩

  6. Higher-order Organization of Complex Networks ↩

  7. 原始的通过图的点之间的邻接矩阵定义的Laplacian矩阵的特征值满足 ϕ∗22≤λ2≤2ϕ∗ ↩


report

Recommend

About Joyk


Aggregate valuable and interesting links.
Joyk means Joy of geeK