【密码学】椭圆曲线密码ECC

ComyDream Studio

RSA密钥长度太长，计算较慢。亲，来试试ECC吧！

椭圆曲线密码学（Elliptic Curve Cryptography，ECC）是一种基于椭圆曲线数学的非对称加密算法，安全性基于椭圆离散对数问题。

优势：ECC 使用较短的密钥就能达到与更长密钥的 RSA 相当等级的安全性。被广泛用于 HTTPS、SSH、PGP 协议以及比特币（BTC）、以太币（ETH）上。

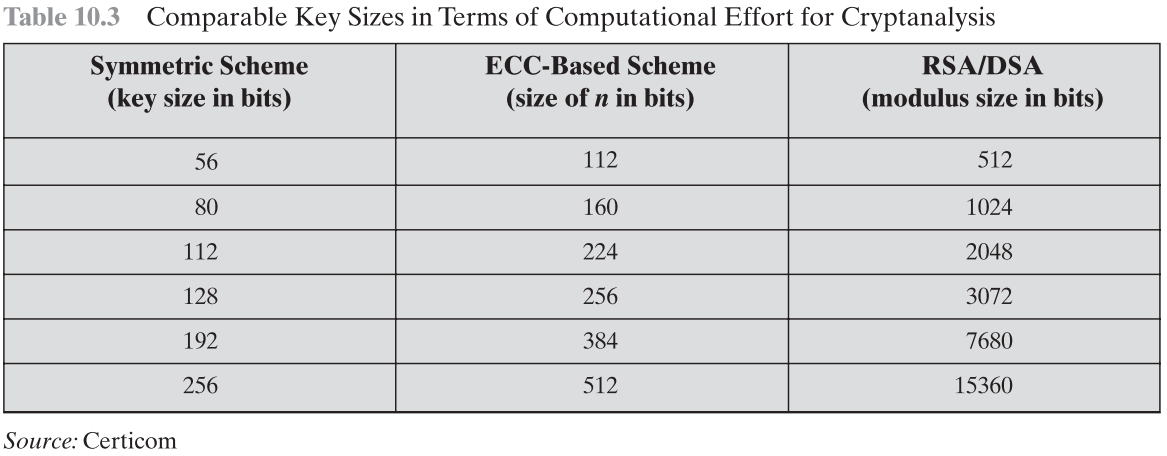
ECC 有取代 RSA 的趋势，ECC 是下一代非对称加密算法！

缺陷：可能被 NSA 藏了后门，可信度还没有 RSA 高，而且可能涉及专利。

万恶的 mdgzy！

椭圆曲线 E(a,b) 由如下形式的方程定义：

y2=x3+ax+b

并且要保证曲线不含奇点，即满足：

4a3+27b2≠0

椭圆曲线始终关于 x 轴对称。

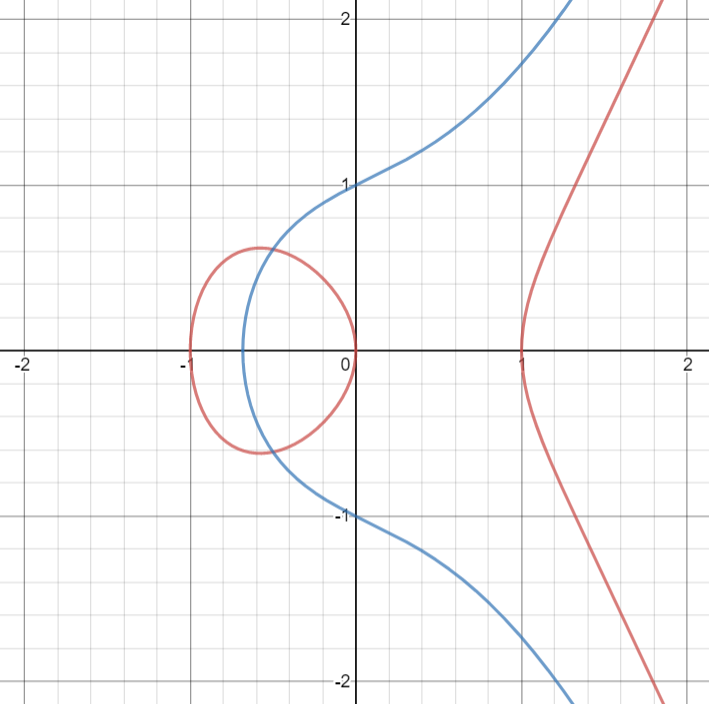
图中，红色为 y2=x3−x，蓝色为 y2=x3+x+1，作图工具：Desmos。

另外，椭圆曲线还需引入一个无穷处的点作为曲线的一部分，可以使用符号 O 表示。

那么，椭圆曲线的表达式为：

{(x,y)∈R2 | y2=x3+ax+b, 4a3+27b2≠0} ∪ {O}

一个群（group）G 由一堆元素和一个运算（加法 +）组成，必须满足四个条件：

• 封闭性：若 a∈G 且 b∈G，则 a+b∈G
• 结合律：若 a,b,c∈G，则 (a+b)+c=a+(b+c)
• 单位元：对于每个 a∈G，a+O=O+a=a
• 逆元：对于每个 a∈G，都存在唯一的 b∈G，使得 a+b=O，称 b 为 a 的逆元

若一个群满足交换律，即 a+b=b+a，则称它为交换群或阿贝尔群。

若满足群的条件，则可以直接使用群的性质。比如，只有一个单位元，每个元素有且只有一个逆元。

椭圆曲线上的群论

可以在椭圆曲线上定义一个阿贝尔群：

• 群中的元素是椭圆曲线上的点
• 单位元是无穷处的点 O
• (x,y) 的逆元是 (x,−y)
• 加法规则：一条直线与 E 交于三个点 P,Q,R，它们之和等于 O，即 P+Q+R=O
• + 运算满足交换律、结合律

加法的几何描述

由 P+Q+R=0 有：

P+Q=−R

也就是做穿过 P 和 Q 两点的直线，它穿过的第三个点 R=(x,y) 的关于 x 轴对称的点 (x,−y) 就是 P+Q 的结果。

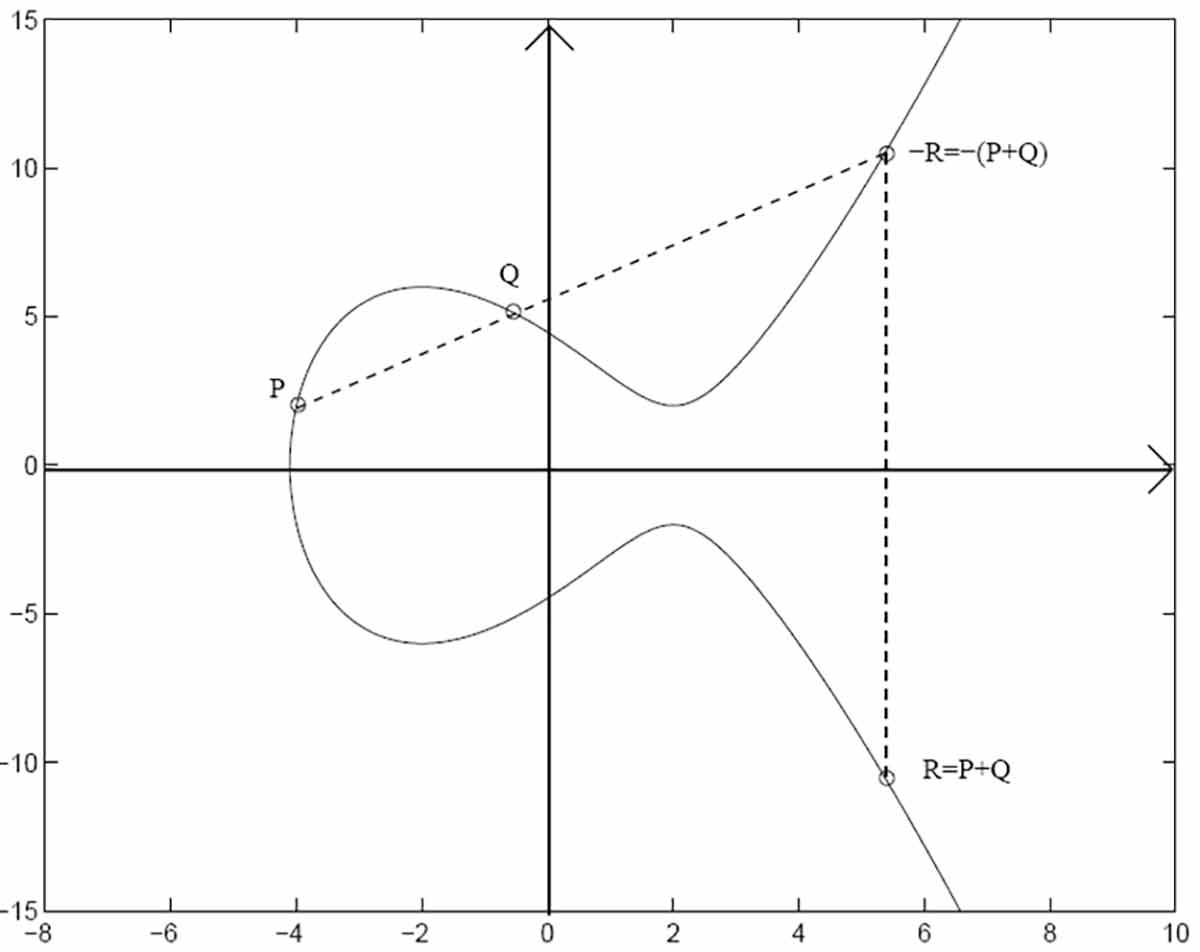
若 P=Q，那么这条直线是过点 P 的切线。

实数域上加法的代数描述

一元三次方程的解，直接用公式吧少年。（老师都不想细讲）

椭圆曲线公式：

y2=x3+ax+b

当P≠Q时：

Δ=yQ−yPxQ−xPxR=Δ2−xP−xQyR=−yP+Δ(xP−xR)

当P=Q时：

xR=(3x2P+a2yP)2−2xPyR=(3x2P+a2yP)(xP−xR)−yP

Zp上加法的代数描述

设变元x,y和椭圆曲线参数a,b都在Zp上取值，椭圆曲线公式两边取模p得到Ep(a,b)：

y2modp=(x3+ax+b)modp

求P+Q：

xR=(λ2−xP−xQ)modpyR=(λ(xP−xR)−yP)modp λ={(yQ−yPxQ−xP)modp if P≠Q(3x2P+a2yP)modp if P=Q

GF(2m)上加法的代数描述

设变元x,y和椭圆曲线参数a,b都在GF(2m)上取值，得到E2m(a,b)：

y2+xy=x3+ax2+b

大型懵逼现场！反正考试也不太可能会考。

若P=(xP,yP)，则−P=(xP,xP+yP)。

若P≠Q, P≠−Q, R=P+Q，则：

λ=yQ+yPxQ+xPxR=λ2+λ+xP+xQ+ayR=λ(xP+xR)+xR+yP

若R=P+P，则：

λ=xP+yPxPxR=λ2+λ+ayR=x2P+(λ+1)xR

伽罗瓦域可以极大扩展可能取值？

ECC的安全性基于椭圆曲线上的离散对数问题，考虑方程Q=kP：

• 已知k,P，计算Q容易
• 已知P,Q，计算k困难

ECC Diffie-Hellman

和ElGamal一样，它的安全性也基于离散对数问题，很快想到，可以往DH上套：

1. 选定一个大的模数q（两种形式：素数p或2m，分别对应上面两种域）以及系数a和b，由此定义椭圆曲线Eq(a,b)，并在其上挑选一个基点G=(xg,yg)，它的阶n（使得nG=O成立的最小正整数）是一个非常大的数。Eq(a,b)和G均公开。
2. Alice选择一个小于n的整数nA作为私钥，计算公钥PA=nAG并公开
3. Bob选择一个小于n的整数nB作为私钥，计算公钥PB=nBG并公开
4. Alice计算密钥K=nAPB=(nAnB)G，Bob计算密钥K=nBPA=(nAnB)G。

这样，Alice和Bob就通过不安全信道建立起了密钥K。

注意：上述过程中的加法、数乘运算均是椭圆曲线下的运算。

ECC 加解密

和ElGamal一样，本质上就是通过DH协商一个密钥，然后用这个密钥进行加解密。

密钥生成：

1. 协商椭圆曲线Eq(a,b)和基点G=(xg,yg)
2. Alice选择一个私钥nA，计算公钥PA=nAG并公开
3. Bob选择一个私钥nB，计算公钥PB=nBG并公开

假设Bob要给Alice发一个消息M：

1. Bob使用自己的私钥nB和Alice的公钥PA计算共同密钥K=nBPA=(nAnB)G
2. Bob发送c1=PB, c2=K+M

Alice收到密文，解密过程：

1. Alice计算共同密钥K=nAc1=nAPB=(nAnB)G
2. Alice解密消息M=c2−K

若K=(xK,yK)，则−K=(xk,−yK)。

再次提醒：上述过程中的加法、数乘运算均是椭圆曲线下的运算。

Online Calculator

ECCalculator - christelbach - Zp下的加法

Python Code

1. def ecAdd(P, Q, a, b, p):
2. x_P, y_P = P
3. x_Q, y_Q = Q
4. if P == Q:
5. lmd = (3*x_P*x_P+a)*pow(2*y_P,-1,p)%p
6. elif x_P == x_Q:
7. return (0, 0)
8. else:
9. lmd = (y_Q-y_P)*pow(x_Q-x_P,-1,p)%p
10. x_R = (lmd*lmd-x_P-x_Q)%p
11. y_R = (lmd*(x_P-x_R)-y_P)%p
12. return (x_R, y_R)
13. def ecTimes(n, P, a, b, p):
14. R = P
15. for i in range(2, n+1):
16. R = ecAdd(P, R, a, b, p)
17. # print('{}P = ({}, {})'.format(i, R[0], R[1]))
18. return R

椭圆曲线数乘运算 ecTimes() 可用类似快速幂的形式优化，但本人懒，就酱。

密码编码学与网络安全——原理与实践（第七版）

椭圆曲线密码学 - Wikipedia

ECC椭圆曲线加密算法介绍 - 知乎

终于知道本科的时候为什么不学且不考ECC了：

• 看着很玄学
• 推导略复杂
• 做题套公式，计算复杂且易出错

说实话我觉得把公式贴在这里都是浪费时间。

读书患不多，思义患不明，患足己不学。既学患不行。

本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明来自 ComyDream 。
本文链接：http://comydream.github.io/2020/12/20/cryptography-ecc/