梯度下降算法的Python实现

1.梯度下降算法的理解

我们在求解最优化问题的时候，需要最小化或最大化某一个目标函数。如线性回归中，就需要最小化残差平方和。

某一向量的平方和函数可定义如下：

def sum_of_squares(v):
    """computes the sum of squared elements in v"""
    return sum(v_i ** 2 for v_i in v)

若f(x,y,z)在点P0(x0,y0,z0)存在对所有自变量的偏导数，则称向量(fx(P0),fy(P0),fz(P0))为函数f在点P0的梯度,记为：

grad f=(fx(P0),fy(P0),fz(P0))

由于某一方向上l的方向导数公式可以写成

fl(P0)=|grad f(P0)|cosθ

其中，θ为梯度向量grad f(P0)与l方向上的单位向量l0的夹角。

从而，当f可微时，f在P0的梯度方向是f的值增长最快的方向。

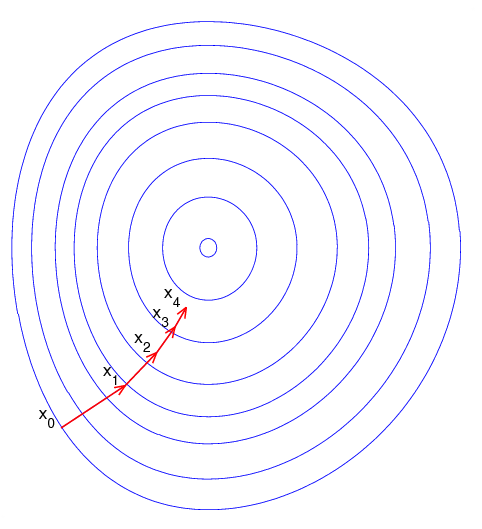
梯度下降算法的直观理解

由于梯度方向是使得函数值下降最快的方向,从而快速求解到目标函数最小值的一种途径就是：

随机选择一个起点，计算梯度；
朝着负梯度（即使得该点目标函数值下降最快的方向）移动一小步；
重新计算新的位置的梯度，继续朝梯度方向移动一小步
如此循环，直到目标函数值的变化达到某一阈值或者最大迭代次数。

梯度下降算法的局限性

以求解目标函数最小化为例，梯度下降算法可能存在一下几种情况：

当目标函数存在全局最小值时，这种方法可以快速的找到最优解；
当目标函数存在多个局部最小值时，可能会陷入局部最优解。因此需要从多个随机的起点开始解的搜索。
当目标函数不存在最小值点，则可能陷入无限循环。因此，有必要设置最大迭代次数。

2.梯度的估计

梯度的精确计算，需要对目标函数求偏导。

这里，对于一元函数的梯度计算，我们可以采用如下函数进行估计：

from __future__ import division

def difference_quotient(f,x,h):
    return (f(x+h)-f(x))/h

其中，h→0.

对于多元函数，我们可以如下定义梯度估计函数：

# 先定义偏导估计函数
def partial_difference_quotient(f,v,i,h):
    """compute the i-th partial difference quotient of f at v"""
    w = [v_j + (h if j==i else 0)
            for j,v_j in enumerate(v)]
    return (f(w)-f(v))/h

# 再定义梯度估计函数
def estimate_gradient(f,v,h=0.00001):
    return [partial_difference_quotient(f,v,i,h)
           for i,_ in enumerate(v)]

3.梯度的使用

这里，先通过一个简单的例子测算梯度下降算法是否有效。

假设我们要求解的目标函数是：Min f(X)=XTX,其中，X为一个三维的向量。则其梯度为2X,不难计算出其最小值点为[0,0,0].

下面，通过梯度下降法来求解。

### 定义步长函数

def step(v,direction,step_size):
    """move step_size in the direction from v"""
    return [v_i + step_size * direction_i 
                   for v_i,direction_i in zip(v,direction)]

### 定义梯度
def sum_of_squares_gradient(v):
    return [2 * v_i for v_i in v]

import random

### 选择一个随机的起点
v = [random.randint(-10,10) for i in range(3)]

### 定义向量距离
#######################
#### 减法定义
def vector_substract(v,w):
    """substracts coresponding elements"""
    return [v_i - w_i
                   for v_i,w_i in zip(v,w)]

### 向量的点乘
def dot(v,w):
    return sum(v_i * w_i 
                      for v_i,w_i in zip(v,w))


### 向量的平房和
def sum_of_squares(v):
    """v_1*v_1+v_2*v_2+...+v_n*v_n"""
    return dot(v,v)


### 向量的距离
##### method 1:
def distance(v,w):
    """"""
    return sum_of_squares(vector_substract(v,w))

### 进行迭代计算
tolerance = 0.000000001
max_iter = 1000000
iter = 1

while True:
    gradient = sum_of_squares_gradient(v)
    next_v = step(v,gradient,-0.01)
    if (distance(next_v,v) < tolerance) or (iter > max_iter) :
        break
    v = next_v
    iter += 1
    
print v,iter

[0.0007944685438825013, -0.00026482284796083356, -0.0013241142398041702] 443

4.选择合适的步长

虽然我们已经明确要沿着梯度的方向移动，然而移动的步长究竟为多少比较合适，却没有一个通用的标准。因此，步长的选择是一门基于经验的艺术。

以下是几种主流的步长选择方法：

使用固定步长；
逐步压缩步长；
每一步的步长选择通过最小化目标函数来确定。

最后一种似乎听起来较为合理，但是也是最为耗时的。我们可以退而求其次：每一步的迭代步长通过从几个有限离散的候选步长中来确定。

step_sizes = [100,10,1,0.1,0.01,0.001,0.0001,0.00001]

但是步长的选择范围过广也可能造成另一个问题：自变量的输入值可能超过定义域的范围。因此，需要定义一个safe函数来避免这种情况的出现。假设我们要求的是目标函数最小化，则可以将『自变量的输入值超过定义域的范围』这种情况的目标函数值设为无穷大。从而使得这种步长不会被考虑。

def safe(f):
    def safe_f(*args,**kwargs):
        try:
            return f(*args,**kwargs)
        except:
            return float('inf')
    return safe_f

假设我们的目标函数的定义为最小化target_fn函数，参数的初始值为theta_0,则整个梯度下降算法的实现函数如下：

def minimize_batch(target_fn,gradient_fn,theta_0,tolerance = 0.000001):
    """using gradient descent to find theta that minimizes target function"""
    step_sizes = [100,10,1,0.1,0.01,0.001,0.0001,0.00001]
    
    theta = theta_0
    target_fn = safe(target_fn)
    value = target_fn(theta)
    
    while True:
        gradient = gradient_fn(theta)
        next_thetas = [step(theta,gradient,-step_size)
                          for step_size in step_sizes]
        
    #选择最小化目标函数的theta
    next_theta = min(next_thetas,key = target_fn)
    next_value = target_fn(next_theta)
    
    #停止准则
    if abs((value - next_value)/value) < tolerance:
        return theta,value
    
    else:
        theta,value = next_theta,next_value

#
max_iter = 1000
iter = 1
theta_0 = [random.randint(-10,10) for i in range(3)]

while True:
    theta,value = minimize_batch(target_fn = sum_of_squares,gradient_fn = sum_of_squares_gradient,theta_0 = theta_0,tolerance = 0.0001)
    if (iter < max_iter) or (value == sum_of_squares(theta_0)):
        break
    theta_0 = theta
    iter+=1

    
print theta,iter

当我们的优化问题是最大化目标函数时，可做如下修改。

def negate(f):
    """return a function that for any input x returns -f(x)"""
    return lambda *args,**lwargs:-f(*args,**kwargs)


def negate_all(f):
    """the same when f returns a list of numbers"""
    return lambda *args,**kwargs:[-y for y in f(*args,**kwargs)]

def maximize_batch(target_fn,gradient_fn,theta_0,tolerance = 0.000001):
    return minimize_batch(negate(target_fn),
                         negate_all(gradient_fn),
                         theta_0,
                         tolerance)

6.随机梯度下降

很多时候，我们要处理的目标函数是线性可加的，即目标函数形式为：

f(ω)=n∑i=1fi(ω,xi,yi)

此时，梯度下降算法的迭代公式为：

ωt+1=ωt−ηt+1n∑i=1▽fi(ωt,xi,yi)

如果我们面对的是一个n非常大的数据集，在每一步的迭代中，由于要计算所有点的梯度▽fi，这样会非常耗时。

而随机梯度下降算法的基本思想是：每次迭代时，随机选择一个点的梯度▽fi来代替▽f.此时，有：

ωt+1=ωt−ηt+1▽fik(ωt,xik,yik),ik∈1,2,3,...,n

之所以可以这么做，是因为E[▽fik(ωt,xik,yik)]=▽f(ωt)。当ηt=O(1/t),算法在期望的意义下收敛。

import random

def in_random_order(data):
    """generator that returns the elements of data in random order"""
    indexes = [i for i,_ in enumerate(data)]
    random.shuffle(indexes)
    for i in indexes:
        yield data[i]

??random.shuffle

为了避免陷入无限循环，当目标函数没有得到优化时，则逐步缩短步长。

def minimize_stochastic(target_fn,gradient_fn,x,y,theta_0,alpha_0=0.01):
    data = zip(x,y)
    theta = theta_0
    alpha = alpha_0   # 初始化步长
    min_theta, min_value = None,float("inf")
    iterations_with_no_improvment = 0
    
    #当迭代100次均没有提升，则停止
    while iterations_with_no_improvment < 100:
        value = sum(target_fn(x_i,y_i,theta) for x_i,y_i in data)
        
        if value < min_value:
            #found a new minimum,remember it
            min_theta,min_value = theta,value
            iterations_with_no_improvment = 0
            alpha= alpha_0
        else:
            iterations_with_no_improvment+=1
            alpha *=0.9
            
        #沿着梯度移动一步
        for x_i,y_i in in_random_order(data):
            gradient_i = gradient_fn(x_i,y_i,theta)
            theta = vector_substract(theta,scalar_multiply(alpha,gradient_i))
            
    return min_thata

『Data Science from Scratch』
『数学分析』——方向导数与梯度
随机梯度下降法到底是什么？

梯度下降算法的Python实现

梯度下降算法的Python实现

1.梯度下降算法的理解

梯度下降算法的直观理解

梯度下降算法的局限性

2.梯度的估计

3.梯度的使用

4.选择合适的步长

6.随机梯度下降

Recommend

0CTF 2018 Writeup

基于图搜索的路径规划算法(一)：Dijkstra 和 A*

Introduction to ML Services on Azure HDInsight | Microsoft Docs

算法 | 全排列问题

Dumping Domain Password Hashes

Bag of Freebies (Arxiv, 2019)

regexp注入

Matplotlib 系列：网格数据与 pcolor

Redis GEO 相关命令简介

CTF做题总结(二)

About Joyk