

快速傅立叶变换(FFT)在整数乘法中的应用
source link: https://lasttillend.github.io/algorithm,/divide/and/conquer/2020/05/30/dc_for_integer_multiplication_using_fast_fourier_transforms.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

在上一篇博文中,我们谈到了一种利用分治法优化整数乘法的算法,它的时间复杂度约为O(n1.59),而本文将介绍另一种基于快速傅立叶变换(Fast Fourier Transform, FFT)的整数乘法,它的时间复杂度更低,为O(nlogn)。这个方法将整数乘法和多项式乘法联系起来,而后者可以利用快速傅立叶变换进行计算。值得注意的是,在快速傅立叶变换的实现算法中,我们将再次看到分治思想的身影。
整数乘法转化为多项式乘法
首先,我们建立整数乘法和多项式乘法的联系。举一个简单的例子,假设x=123456。若以十为底,则可以将它写成: 123456=6×100+5×101+4×102+3×103+2×104+1×105, 所以,整数123456可以和多项式6+5x+4x2+3x3+2x4+x5对应,而该多项式又可以由它的系数向量[6,5,4,3,2,1]表示。它们的转换代码如下所示。
def int_to_poly(x, base=10):
"""
Args:
x: int, integer to be represented as a polynomial
bast: int
Returns:
a list containing the coefficients of the corresponding polynomial
"""
if x == 0:
return [0]
x = abs(x)
p = []
while x > 0:
x, r = divmod(x, base)
p.append(r)
return p
int_to_poly(123456, base=10)
输出结果:
[6, 5, 4, 3, 2, 1]
def poly_to_int(p, base=10):
"""
Args:
p: list, polynomial representation of an integer
base: int
Returns:
the integer represented by p
"""
n = len(p)
return sum([d * base ** (n - 1 - i) for i, d in enumerate(p[::-1])])
poly_to_int([6, 5, 4, 3, 2, 1], base=10)
输出结果:
另外,将整数乘法和多项式乘法都写成竖式,可以发现它们是类似的:
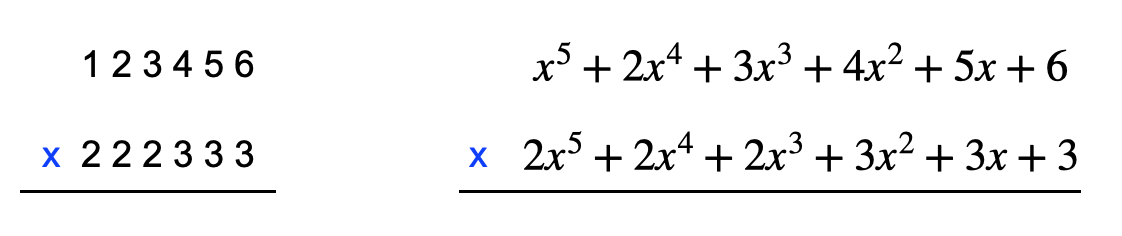
所以,接下来我们只需要考虑多项式之间的乘法即可。
FFT视角下的多项式乘法
假设我们有两个d次多项式:
A(x)=a0+a1x+a2x2+⋯+adxdB(x)=b0+b1x+b2x2+⋯+bdxd.
它们的乘积是一个2d次多项式:
C(x)=c0+c1x+c2x2+⋯+c2dx2d,
其中,ck=a0bk+a1bk−1+⋯akb0=∑ki=0akbk−i。
关于多项式C的表示方法,除了可以用一个2d+1维的系数向量[c0,c1,⋯,c2d]表示以外,还可以用它在2d+1个点上的取值来表示,即
C(x0),C(x1),⋯,C(x2d)
唯一决定了C,这叫做多项式的值表示法(value representation)。我们希望尽可能快速地计算出这些值,然后再将C还原成系数表示的形式。注意到C(xk)=A(xk)B(xk),所以问题的关键是计算A(xk)和B(xk),也就是如何将一个多项式从系数表示法转换成值表示法,这个过程称为evaluation,而前面提到的从值表示法还原成系数表示法则称为interpolation。
多项式乘法的算法如下:
算法1:多项式乘法
--------------
输入:d次多项式 A(x) 和 B(x)
输出:乘积C = A ⋅ B
Selection:
挑选点x_0, x_1, x_2, ⋯, x_(n-1) ( n >= 2d + 1)
Evaluation:
计算 A(x_0), A(x_1), ⋯, A(x_(n-1))和B(x_0), B(x_1), ⋯, B(x_(n-1))
Multiplication:
计算 C(x_k)=A(x_k)B(x_k), k = 0, ⋯, n - 1
Interpolation:
还原 C(x) = c_0 + c_1x + ⋯ + c_(2d)x^(2d)
注意,这里取超过2d+1个点看似是浪费时间,但是不影响结果,并且接下来会看到,通过取超过2d+1的最小的2的幂次个点可以大大简化计算。
1. Evaluation
在Evaluation阶段,我们的目标是快速计算n个值:A(x0),A(x1),A(xn−1)。为了达成这个目标,我们必须挑选便于计算或者能重复利用已知计算结果的点。那么,多项式有什么特性吗?仔细思考后不难发现,偶数次幂的结果对于±x都相同,而奇数次幂则正好相反。于是,一个自然而然的想法是挑选n个正负配对的点 ±x0,±x1,⋯,±xn/2−1, 这样计算A(xi)和A(−xi)时就存在大量重复之处,我们只需计算一次偶数次幂和奇数次幂即可。
举一个例子,假设n=8, A(x)=3+4x+6x2+2x3+x4+10x5−2x6+2x7,于是
A(x)=(3+6x2+x4−2x6)+x(4+2x2+10x4+2x6)=Ae(x2)+xAo(x2),
A(−x)=(3+6x2+x4−2x6)−x(4+2x2+10x4+2x6)=Ae(x2)−xAo(x2).
这里,Ae(x)=3+6x+x2−2x3,Ao(x)=4+2x+10x2+2x3。
可以看到,通过奇偶分项既可以降低次数,又可以重复利用Ae和Ao的计算结果。分拆后又合并,这不就是分治思想吗?没错,evaluation阶段的核心思想就是分治!
上面的讨论告诉我们挑选的点要正负配对(保证x2相同),这样只需要计算次数仅为原来一半的Ae和Ao就可以得到A(x)和A(−x)。为了能对Ae和Ao做同样的操作,我们必须保证挑选的点经过平方以后仍然要是正负配对的!也就是说,x4要相同,而配对组数只有原来的一半(因为次数降低,所需要的点只有原来的一半),如下图所示:
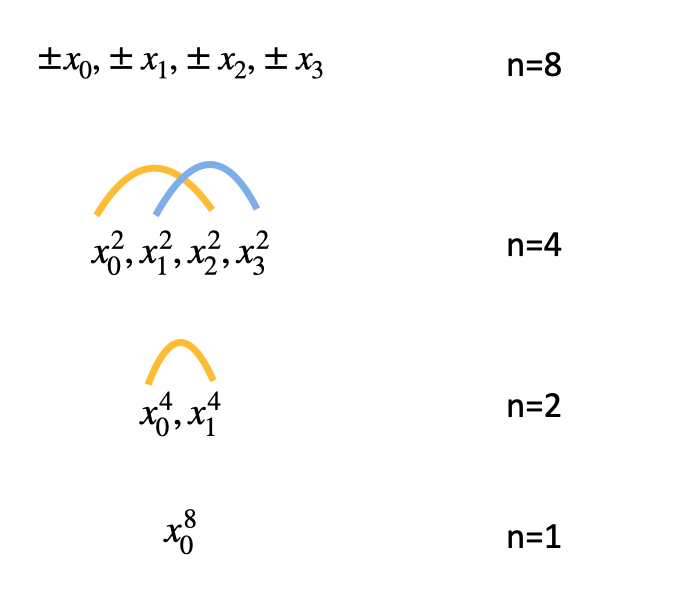
上面的图告诉我们,假设一开始有4组正负匹配,经过平方后得到2组正负匹配,再平方得到1组正负匹配,最后一次平方得到一个数,也就是递归的出口(base case)。接下来考虑base case要取什么值好。首先排除0,因为每一轮都有正负匹配的要求,如果用了0,那每一轮的点都是0了。而除了0以外,最简单的数就是1了,没错,就是它了!我们取最后一个点x80为1,则x40和x41为1的二次方根,一路往上推,x20,x21,x22,x23为1的四次方根,±x0,±x1,±x2,±x3为1的八次方根,所以我们一开始要找的8个点就是z8=1的根!推广到任意情形,即找zn=1的根。
zn=1的n个根叫做“complex nth roots of unity”,依次为1,ω,ω2,⋯,ωn−1,其中,ω=e2πi/n。如果一开始n是2的幂次,那么在接下来的每一轮递归会依次得到”(n/2k)-th root of unity”, k=1,2,3,⋯,这些点均正负匹配,可以利用分治法快速计算多项式在这些点上的取值。这就是快速傅立叶变换(FFT)。
FFT算法如下:
算法2: FFT
----------
输入:多项式A(x)的系数,该多项式次数<=n-1, n为2的幂次;
omega, n-th root of unity
输出:值表达形式 A(omega^0), A(omega^1), ... , A(omega^(n-1))
if omega = 1: return A(1)
拆分A(x) = A_e(x^2) + x A_o(x^2)
调用FFT(A_e, omega^2)得到 A_e在omega的偶次幂处取值
调用FFT(A_o, omega^2)得到 A_o在omega的偶次幂处取值
for j = 0 to n - 1:
计算 A(omega^j) = A_e(omega^2j) + omega^j A_o(omega^2j)
return A(omega^0), A(omega^1), ..., A(omega^(n-1))
FFT是一种分治算法,假设它的时间为T(n),则 T(n)=2T(n/2)+O(n).
可见它的时间复杂度为O(nlogn)。
2. Interpolation
通过FFT,我们将多项式从系数表达转换为值表达(Evaluation):
<值>=FFT(<系数>,ω).
反过来从值表达转换为系数表达(Interpolation)也很简单:
<系数>=1nFFT(<值>,ω−1).
FFT既可以用于evaluation,又可以用于interpolation,非常的巧妙。为了证明interpolation的计算式是正确的,我们将从矩阵观点来看看FFT究竟做了哪些操作。
在evaluation阶段,我们其实是将系数向量[a0,a1,⋯,an−1]做了以下线性变换得到值向量[A(x0),A(x1),⋯,A(xn−1]:
[A(x0)A(x1)⋮A(xn−1)]=[1x0x20⋯xn−101x1x21⋯xn−11⋮1xn−1x2n−1⋯xn−1n−1][a0a1⋮an−1],
中间的矩阵M称为Vandermonde矩阵,它有如下性质:当x0,x1,⋯,xn−1相异时可逆。
在Interpolation阶段,需要计算M−1。这里的关键点是,由于我们选取的点(n-th root of unity)的特殊性使得这个逆矩阵的计算变得非常容易。
将我们选取的点1,ω,ω2,⋯,ωn−1代入M:
M=Mn(ω)=[111⋯11ωω2⋯ωn−11ω2ω4⋯ω2(n−1)⋮1ωjω2j⋯ω(n−1)j⋮1ω(n−1)ω2(n−1)⋯ω(n−1)(n−1)].
Claim: Mn(ω)−1=1nMn(ω−1).
证明过程主要分两步,首先证明M的列两两正交,于是MM∗=M∗M=nI;第二步计算M∗,主要用到ω的共轭 ˉω=ω−1,所以M∗=Mn(ω−1)。
3. 从矩阵角度近距离观察FFT
接下来让我们从矩阵角度观察FFT并改写算法2。将矩阵Mn(ω)的偶数列和奇数列重新排序,偶数列放到最前列,相应地,系数向量a的偶数位也放到最前列。此时可以将Mn(ω)划分成四块:偶数列分为上下相等的两块,奇数列分为上下相反的两块,如下图所示。这里需要用到下面两个式子:
ω2k(j+n/2)=ω2jk+nk=ω2jk,ω(2k+1)(j+n/2)=ω2k(j+n/2)ωj+n/2=ω2jk⋅ωj⋅ωn/2=−ωjω2jk.
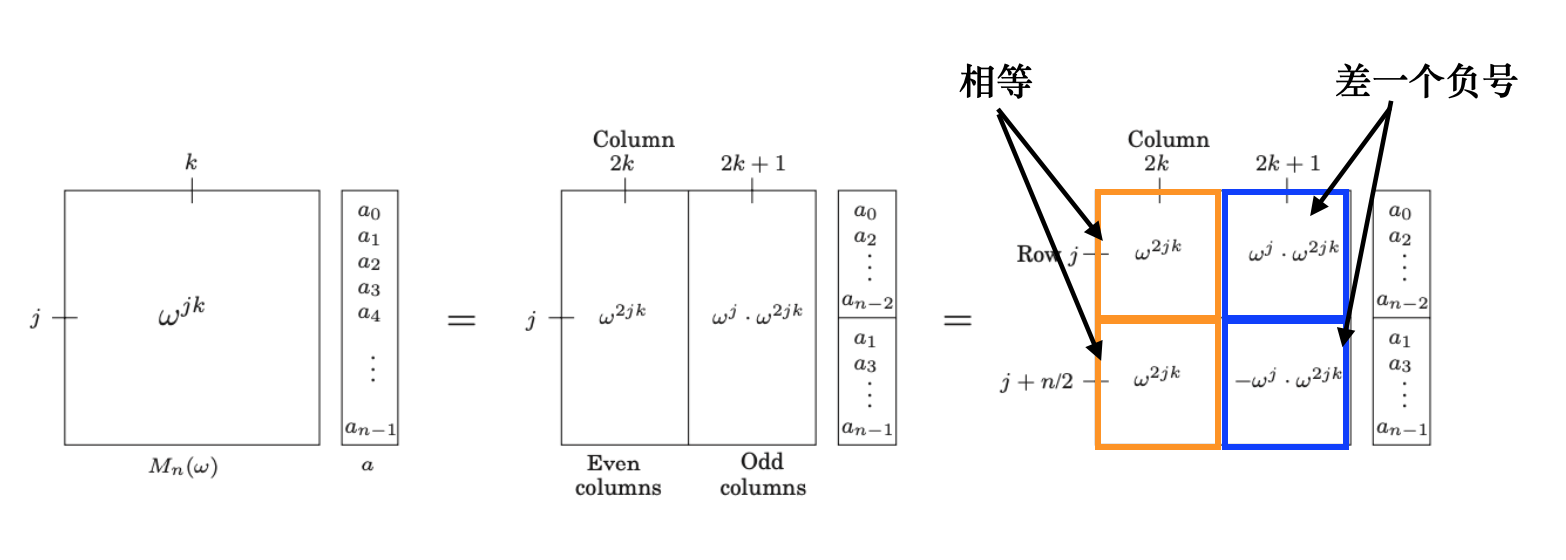
因为ω2jk=(ωjk)2,所以这四个小块其实都和Mn/2(ω2)有关,如下图所示:
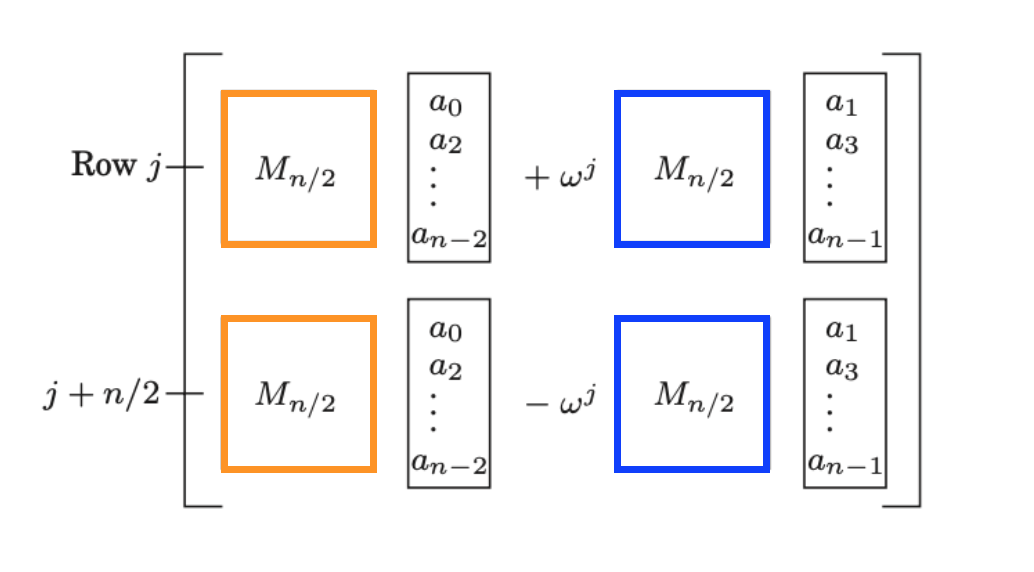
改写后的FFT算法2为:
算法2': FFT
----------
输入:多项式A(x)的系数向量a=(a_0, a_1, ..., a_(n-1)),该多项式次数<=n-1, n为2的幂次;
omega, n-th root of unity
输出:M_n(omega)a
if omega = 1: return a
(s_0, s_1, ..., s_(n/2-1)) = FFT((a_0, a_2, ..., a_(n-2)), omega^2)
(s'_0, s'_1, ..., s'_(n/2-1)) = FFT((a_1, a_3, ..., a_(n-1)), omega^2)
for j = 0 to n/2 - 1:
r_j = s_j + omega^j s'_j
r_(j + n/2) = s_j - omega^j s'_j
return (r_0, r_1, ..., r_(n-1))
from cmath import exp
from math import pi
# A simple class to simulate n-th root of unity
# This class is by no means complete and is implemented
# merely for FFT and FPM algorithms
class NthRootOfUnity:
def __init__(self, n, k = 1):
self.k = k
self.n = n
def __pow__(self, other):
if type(other) is int:
n = NthRootOfUnity(self.n, self.k * other)
return n
def __eq__(self, other):
if other == 1:
return abs(self.n) == abs(self.k)
def __mul__(self, other):
return exp(2*1j*pi*self.k/self.n)*other
def __repr__(self):
return str(self.n) + "-th root of unity to the " + str(self.k)
@property
def th(self):
return abs(self.n // self.k)
def FFT(A, omega):
"""
The fast Fourier transform algorithm. The time complexity is O(n logn).
Args:
A: an array of integers of size n representing a polynomial
omega: a root of unity
Returns:
[A(omega), A(omega^2), ..., A(omega^(n-1))]
"""
if omega == 1:
return [sum(A)] # A(1)
o2 = omega ** 2
s = FFT(A[0::2], o2) # even
s_prime = FFT(A[1::2], o2) # odd
r = [None] * omega.th
for i in range(omega.th // 2):
r[i] = s[i] + omega ** i * s_prime[i]
r[i+omega.th//2] = s[i] - omega ** i * s_prime[i]
return r
def FPM(A, B):
"""
The fast polynomial multiplication algorithm.
Args:
A, B: two arrays of integers representing polynomials, their length is in O(n).
Returns:
coefficient representation of AB.
"""
n = 1 << (len(A) + len(B) - 2).bit_length()
o = NthRootOfUnity(n)
AT = FFT(A, o)
BT = FFT(B, o)
C = [AT[i] * BT[i] for i in range(n)]
D = [round((a / n).real) for a in FFT(C, o ** -1)]
while len(D) > 0 and D[-1] == 0:
del D[-1]
return D
def FFT_int_multiply(x, y):
"""
Integer multiplication using Fast Fourier transform.
Args:
x, y: integers
Returns:
product of x and y
"""
if x == 0 or y == 0:
return 0
elif (x > 0 and y > 0) or (x < 0 and y < 0):
sign = 1
else:
sign = -1
x = abs(x)
y = abs(y)
A = int_to_poly(x, base=10)
B = int_to_poly(y, base=10)
C = FPM(A, B)
z = poly_to_int(C)
return sign * z
Reference
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK