您可能感兴趣的文章推荐 💜《夜深人静写算法》💜

  很多人加我都是想询问如何学好算法。我的方法是我用了 十年 的时间，自己总结出来的，不可能适合所有人，但是我觉得挺有效的，如果你觉得可行，尽管一试！
  首先，我们心中要有一团🔥火🔥，一团希望之🔥火🔥！只要你心中充满希望，即使是死去的意志也会在你内心复活。
  「 动态规划 」作为算法中一块比较野的内容，没有比较系统的分类，只能通过不断总结归纳，对各种类型进行归类。「 动态规划 」（即 Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学 以及 生物信息学中使用的，通过把原问题分解为相对简单的「 子问题 」的方式求解「 复杂问题 」的方法。
  「 动态规划 」是一种算法思想：若要解一个给定问题，我们需要解其不同部分（即「 子问题 」），再根据「 子问题 」的解以得出原问题的解。要理解动态规划，就要理解 「 最优子结构 」 和 「 重复子问题 」。
  本文将针对以下一些常用的动态规划问题，进行由浅入深的系统性讲解。首先来看一个简单的分类，也是今天本文要讲的内容。

一、递推问题

  递推问题作为动态规划的基础，是最好掌握的，也是必须掌握的，它有点类似于高中数学中的数列，通过 前几项的值 推导出 当前项的值。

1、一维递推

  你正在爬楼梯，需要 n n n 阶你才能到达楼顶。每次你可以爬 1 1 1 或 2 2 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

  假设我们已经到了第 n n n 阶楼梯，那么它可以是从 n − 1 n-1 n−1 阶过来的，也可以是从 n − 2 n-2 n−2 阶过来的（但是，不可能是从 n − 3 n-3 n−3 阶直接过来的），所以如果达到第 n n n 阶的方案数为 f [ n ] f[n] f[n]，那么到达 n − 1 n-1 n−1 阶就是 f [ n − 1 ] f[n-1] f[n−1]，到达 n − 2 n-2 n−2 阶 就是 f [ n − 2 ] f[n-2] f[n−2]，所以可以得出： f [ n ] = f [ n − 1 ] + f [ n − 2 ] f[n] = f[n-1] + f[n-2] f[n]=f[n−1]+f[n−2]  其中，当 n = 0 n=0 n=0 时方案数为 1，代表初始情况； n = 1 n=1 n=1 时方案数为 1，代表走了一步，递推计算即可。
  以上就是最简单的动态规划问题，也是一个经典的数列：斐波那契数列 的求解方式。它通过一个递推公式，将原本指数级的问题转化成了线性的，时间复杂度为 O ( n ) O(n) O(n)。
  C语言代码实现如下：

int f[1000];
int climbStairs(int n){
    f[0] = f[1] = 1;
    for(int i = 2; i <= n; ++i) {
        f[i] = f[i-1] + f[i-2];
    }
    return f[n];
}

2、二维递推

  给定一个非负整数 n n n，生成杨辉三角的前 n n n 行。在杨辉三角中，每个数是它 左上方 和 右上方 的数的和。

  根据杨辉三角的定义，我们可以简单将上面的图进行一个变形，得到：

于是，我们可以得出以下结论：
  1）杨辉三角的所有数可以存储在一个二维数组中，行代表第一维，列代表第二维度；
  2）第 i i i 行的元素个数为 i i i 个；
  3）第 i i i 行 第 j j j 列的元素满足公式： c [ i ] [ j ] = { 1 i = 0 c [ i − 1 ] [ j − 1 ] + c [ i − 1 ] [ j ] o t h e r w i s e c[i][j] = c[i][j]={1c[i−1][j−1]+c[i−1][j]​i=0otherwise​
  于是就可以两层循环枚举了。时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
  C语言代码实现如下：

int c[40][40];
void generate(int n) {
    for(int i = 0; i < n; ++i) {
        for(int j = 0; j <= i; ++j) {
            if(j == 0 || j == i) {
                c[i][j] = 1;
            }else {
                c[i][j] = c[i-1][j-1] + c[i-1][j];
            }
        }
    }
}

二、线性DP

1、最小花费

  数组的每个下标作为一个阶梯，第 i i i 个阶梯对应着一个非负数的体力花费值 c o s t [ i ] cost[i] cost[i]（下标从 0 开始）。每当爬上一个阶梯，都要花费对应的体力值，一旦支付了相应的体力值，就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时，可以选择从下标为 0 0 0 或 1 1 1 的元素作为初始阶梯。

  令走到第 i i i 层的最小消耗为 f [ i ] f[i] f[i]。假设当前的位置在 i i i 层楼梯，那么只可能从 i − 1 i-1 i−1 层过来，或者 i − 2 i-2 i−2 层过来；
    如果从 i − 1 i-1 i−1 层过来，则需要消耗体力值： f [ i − 1 ] + c o s t [ i − 1 ] f[i-1] + cost[i-1] f[i−1]+cost[i−1]；
    如果从 i − 2 i-2 i−2 层过来，则需要消耗体力值： f [ i − 2 ] + c o s t [ i − 2 ] f[i-2] + cost[i-2] f[i−2]+cost[i−2]；
  起点可以在第 0 或者 第 1 层，于是有状态转移方程： f [ i ] = { 0 i = 0 , 1 min ⁡ ( f [ i − 1 ] + c o s t [ i − 1 ] , f [ i − 2 ] + c o s t [ i − 2 ] ) i > 1 f[i] = f[i]={0min(f[i−1]+cost[i−1],f[i−2]+cost[i−2])​i=0,1i>1​

  这个问题和一开始的递推问题的区别在于：一个是求前两项的和，一个是求最小值。这里就涉及到了动态取舍的问题，也就是动态规划的思想。
  如果从前往后思考，每次都有两种选择，时间复杂度为 O ( 2 n ) O(2^n) O(2n)。转化成动态规划以后，只需要一个循环，时间复杂度为 O ( n ) O(n) O(n)。
  C语言代码实现如下：

int f[1024];
int min(int a, int b) {
    return a < b ? a : b;
}
int minCostClimbingStairs(int* cost, int costSize){
    f[0] = 0;
    f[1] = 0;
    for(int i = 2; i <= costSize; ++i) {
        f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]);
    }
    return f[costSize];
}

2、最大子段和

  给定一个整数数组 n u m s nums nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

  由于要求的是连续的子数组，所以对于第 i i i 个元素，状态转移一定是从 i − 1 i-1 i−1 个元素转移过来的。基于这一点，可以令 f [ i ] f[i] f[i] 表示以 i i i 号元素结尾的最大值。
  那么很自然，这个最大值必然包含 n u m s [ i ] nums[i] nums[i] 这个元素，那么要不要包含 n u m s [ i − 1 ] , n u m s [ i − 2 ] , n u m s [ i − 3 ] , . . . , n u m s [ k ] nums[i-1],nums[i-2],nums[i-3],...,nums[k] nums[i−1],nums[i−2],nums[i−3],...,nums[k] 呢？其实就是看第 i − 1 i-1 i−1 号元素结尾的最大值是否大于零，也就是：当 f [ i − 1 ] ≤ 0 f[i-1] \le 0 f[i−1]≤0 时，则 前 i − 1 i-1 i−1 个元素是没必要包含进来的。所以就有状态转移方程： f [ i ] = { n u m s [ 0 ] i = 0 n u m s [ i ] f [ i − 1 ] ≤ 0 n u m s [ i ] + f [ i − 1 ] f [ i − 1 ] > 0 f[i] = f[i]=⎩⎪⎨⎪⎧​nums[0]nums[i]nums[i]+f[i−1]​i=0f[i−1]≤0f[i−1]>0​一层循环枚举后，取 m a x ( f [ i ] ) max(f[i]) max(f[i]) 就是答案了。只需要一个循环，时间复杂度为 O ( n ) O(n) O(n)。
  C语言代码实现如下：

int dp[30010];
int max(int a, int b) {
    return a > b ? a : b;
}

int maxSubArray(int* nums, int numsSize){
    int maxValue = nums[0];
    dp[0] = nums[0];
    for(int i = 1; i < numsSize; ++i) {
        dp[i] = nums[i];
        if(dp[i-1] > 0) {
            dp[i] += dp[i-1];
        }
        maxValue = max(maxValue, dp[i]);
    }
    return maxValue;
}

3、最长单调子序列

  有关最长单调子序列的问题，还有 O ( n l o g 2 n ) O(nlog_2n) O(nlog2​n) 的优化算法，具体方法可以参考以下文章：夜深人静写算法（二十）- 最长单调子序列。

三、二维DP

1、最长公共子序列

  有关于 最长公共子序列 的更多内容，可以参考以下内容：夜深人静写算法（二十一）- 最长公共子序列。

2、最小编辑距离

  有关最小编辑距离的详细内容，可以参考：夜深人静写算法（二十二）- 最小编辑距离。

四、记忆化搜索

  有关记忆化搜索的更多内容，可以参考：夜深人静写算法（二十六）- 记忆化搜索。

五、背包问题

1、0/1 背包

  有关 0/1 背包的更多内容，可以参考：夜深人静写算法（十四）- 0/1 背包。

2、完全背包

  有关完全背包的更多内容，可以参考：夜深人静写算法（十五）- 完全背包。

3、多重背包

  有关多重背包的更多内容，可以参考：夜深人静写算法（十六）- 多重背包。

4、分组背包

  有关分组背包更加详细的内容，可以参考：夜深人静写算法（十七）- 分组背包。

5、依赖背包

  有关依赖背包的更多内容，可以参考：夜深人静写算法（十八）- 依赖背包。

六、树形DP

  给定一棵 n ( n < = 150 ) n(n <= 150) n(n<=150) 个结点的树，去掉一些边，使得正好出现一个 P P P 个结点的连通块。问去掉最少多少条边能够达到这个要求。

  如图所示，一棵 10 个结点的树，我们可以去掉图中红色的边，变成两棵子树，分别为 3 个结点和 7个结点。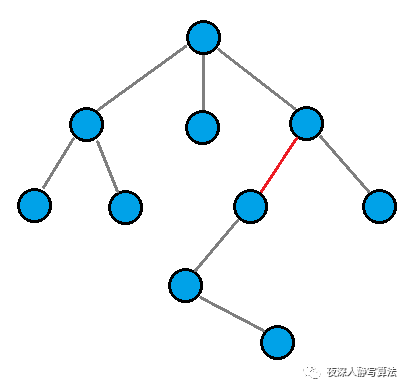

  也可以通过这样的方式，得到三颗子树，分别为 5 、4、1 个结点。

  对于树上的某个结点（如图的红色结点），可以选择去掉连接子树的边，也可以选择留着；每条连接子树的边的 选 和 不选，能够得到一个组合，对应了背包问题，而每棵子树的选择只能选择一种，对应了分组背包，所以可以利用这个思路来设计状态。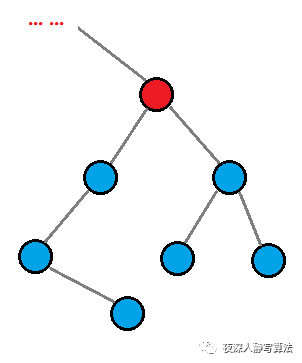

  状态设计：用 d p [ u ] [ x ] dp[u][x] dp[u][x] 表示以 u u u 为根的子树，能够通过去掉一些边而得到一个正好是 x x x 结点的连通块（注意只包含它的子树的部分，不连接它的父结点）的最少消耗；
  状态转移思路：枚举 u u u 的所有子结点，对于子结点 v v v，递归计算 d p [ v ] [ i ] ( 1 < = i < = x ) dp[v][i] (1 <= i <= x) dp[v][i](1<=i<=x) 所有的可能情况，如果 d p [ v ] [ i ] dp[v][i] dp[v][i] 存在，则认为这是一个容量为 i i i，价值为 d p [ v ] [ i ] dp[v][i] dp[v][i] 的物品，表示为 ( i , d p [ v ] [ i ] ) (i, dp[v][i]) (i,dp[v][i])。然后在结点 u u u 的背包上进行一次分组背包。
  初始情况：对于任何一个结点 u u u，它的子结点个数为 c u c_u cu​，初始情况是 d p [ u ] [ 1 ] = c u dp[u][1] = c_u dp[u][1]=cu​，表示如果以当前这个结点为孤立点，那么它的子树都不能选，所以费用就是去掉所有连接子树的边，即子树的个数。
  状态转移：然后对于每棵子树 v v v 的 k k k 个结点的连通块，答案就是 d p [ v ] [ j − k ] + d p [ v ] [ k ] − 1 dp[v][j-k] + dp[v][k] - 1 dp[v][j−k]+dp[v][k]−1，注意这里的 -1 的含义，因为我们一开始默认将所有连接子树的边去掉，所以这里需要补回来。
  答案处理：最后的答案就是 min ⁡ ( d p [ x ] [ P ] + ( 1   i f   x   i s   n o t   r o o t ) \min(dp[x][P] + (1 \ if \ x \ is \ not \ root) min(dp[x][P]+(1 if x is not root)；考虑结点为 P 的连通块只会出现在两个地方：1）和根结点相连的块，那么答案就是 d p [ r o o t ] [ P ] dp[root][P] dp[root][P]；2）不和根结点相连的块，需要枚举所有结点的 d p [ x ] [ P ] + 1 dp[x][P] +1 dp[x][P]+1 取最小值，其中这里的 1 代表斩断 ( p a r e n t [ x ] , x ) (parent[x], x) (parent[x],x) 这条边的消耗；

七、矩阵二分

  有关矩阵二分的更加深入的内容，可以参考：夜深人静写算法（二十）- 矩阵快速幂。

八、区间DP

  有关区间DP的更深入内容，可以参考：夜深人静写算法（二十七）- 区间DP。

九、数位DP

  对于更加深入的数位DP的实现，可以参考：夜深人静写算法（二十九）- 数位DP。

十、状态压缩DP

  给出 g r a p h graph graph 为有 n ( n ≤ 12 ) n(n \le 12) n(n≤12) 个节点（编号为 0, 1, 2, …, n − 1 n-1 n−1）的无向连通图。 g r a p h . l e n g t h = n graph.length = n graph.length=n，且只有节点 i i i 和 j j j 连通时， j j j 不等于 i i i 时且在列表 g r a p h [ i ] graph[i] graph[i] 中恰好出现一次。返回能够访问所有节点的最短路径的长度。可以在任一节点 开始 和 结束，也可以多次重访节点，并且可以重用边。

  这是一个可重复访问的 旅行商问题。我们可以设计状态如下： f ( s t , e n , s t a t e ) f(st, en, state) f(st,en,state) 代表从 s t st st 到 e n en en，且 经过的节点 的状态组合为 s t a t e state state 的最短路径。
  状态组合的含义是：经过二进制来压缩得到的一个数字，比如 经过的节点 为 0、1、4，则 s t a t e state state 的二进制表示为： ( 10011 ) 2 (10011)_2 (10011)2​ 即 经过的节点 对应到状态 s t a t e state state 二进制表示的位为 1，其余位为 0。
  于是，我们明确以下几个定义：初始状态、最终状态、非法状态、中间状态。

初始状态
  初始状态 一定是我们确定了某个起点，想象一下，假设起点在 i i i，那么在一开始的时候，必然 s t a t e = 2 i state = 2^i state=2i。于是，我们可以认为起点在 i i i，终点在 i i i，状态为 2 i 2^i 2i 的最短路径为 0。也就是初始状态表示如下： f ( i , i , 2 i ) = 0   i ∈ [ 0 , n ) f(i, i, 2^i) = 0 \\ \ \\ i \in [0, n) f(i,i,2i)=0 i∈[0,n)

最终状态
  由于这个问题，没有告诉我们 起点 和 终点，所以 起点 和 终点 是不确定的，我们需要通过枚举来得出，所以最终状态 起点 i i i 和 终点 j j j，状态为 2 n − 1 2^n-1 2n−1（代表所有点都经过，二进制的每一位都为 1）。最终状态表示为： f ( i , j , 2 n − 1 )   i ∈ [ 0 , n ) , j ∈ [ 0 , n ) f(i, j, 2^n-1) \\ \ \\ i \in [0, n), j \in [0, n) f(i,j,2n−1) i∈[0,n),j∈[0,n)

非法状态
  非法状态 就是 不可能从初始状态 通过 状态转移 到达的状态。我们设想一下，如果 f ( i , j , s t a t e ) f(i, j, state) f(i,j,state) 中 s t a t e state state 的二进制的第 i i i 位为 0，或者第 j j j 位 为 0，则这个状态必然是非法的，它代表了两个矛盾的对立面。
  我们把非法状态下的最短路径定义成 i n f = 10000000 inf = 10000000 inf=10000000 即可。 f ( i , j , s t a t e ) = i n f f(i, j, state) = inf f(i,j,state)=inf
  其中 (state & (1<<i)) == 0或者(state & (1<<j)) == 0代表state的二进制表示的第 i i i 和 j j j 位没有 1。

中间状态
  除了以上三种状态以外的状态，都成为中间状态。

  那么，我们可以通过 记忆化搜索，枚举所有的 f ( i , j , 2 n − 1 ) f(i, j, 2^n - 1) f(i,j,2n−1) 的，求出一个最小值就是我们的答案了。状态数： O ( n 2 2 n ) O(n^22^n) O(n22n)，状态转移： O ( n ) O(n) O(n)，时间复杂度： O ( n 3 2 n ) O(n^32^n) O(n32n)。

  关于 「 动态规划 」 的内容到这里就结束了。
  如果还有不懂的问题，可以通过 「 电脑版主页 」找到作者的「 联系方式 」 ，线上沟通交流。

  有关🌳《画解数据结构》🌳 的源码均开源，链接如下：《画解数据结构》

粉丝专属福利

语言入门：《光天化日学C语言》(示例代码)
语言训练：《C语言入门100例》试用版
数据结构：《画解数据结构》源码
算法入门：《算法入门》指引
算法进阶：《夜深人静写算法》算法模板

👇🏻 验证码 可通过搜索下方 公众号 获取👇🏻