How a rigorous programmer can uncover the truth that Richard S. Sutton missed

Not all tunnels are born equal; some can be your tomb. Not all vaccines are born equal; some can revive the epidemic. Not all software are born equal; some can cause air crashes. In this post, I will show you how a rigorous programmer can uncover the truth that even Richard Sutton has missed.

Richard Sutton is a distinguished research scientist at DeepMind and a professor of computing science at the University of Alberta. He is considered one of the founding fathers of modern computational reinforcement learning.

Sutton is also an excellent educator. His textbook Reinforcement Learning: An Introduction, fluid and having a good rythme, is one of my all time favorites.

Recently, I am reading this book for the second time, and I found a thing that Sutton has neglected about the greedy algorithm (described in Chapter 2) for the bandit problem. In this post, I will present my discovery and provide extensive evidence and reasoning to support it. After you finishing reading this post, I hope you to realize the critical role rigorous programming can play.

This post is organized as follows. First, I will present the bandit problem and the greedy approach to crack the problem. Then, I will explain how Sutton’s “clever” computational device ended with misguiding him and led him to believe something false. Finally, I will compare my implementation with the others’ as well as provide extensive experiment results to support my findings. This discovery is original, just like all my other posts.

The bandit problem

The bandit problem is a classic one in reinforcement learning, and it is usually the first item taught. The bandit is actually a machine, which has a better-known name as the slot machine.

The machine shown above has only one arm, whereas the bandit machine in reinforcement learning has multiple arms, with each arm having a different reward distribution. For example, the following figure shows the reward distribution of a ten-armed bandit.

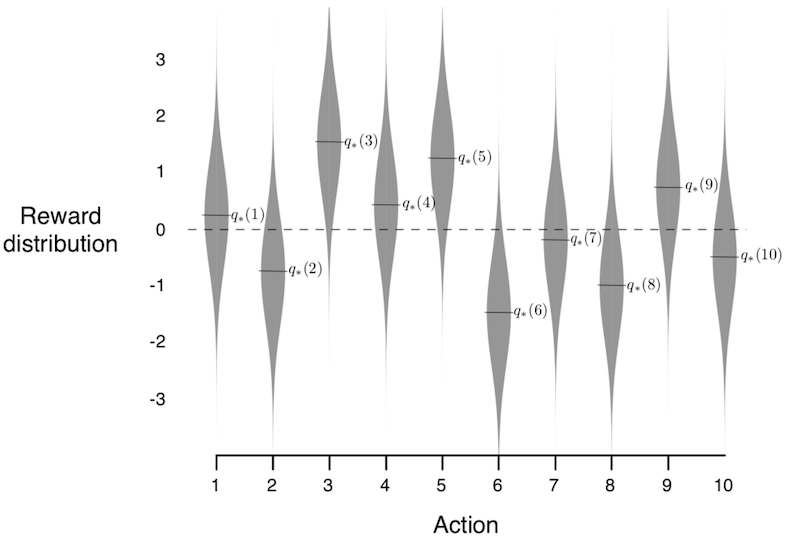
Obviously, the proprietor of the casino will not tell you the distribution. You have to find the optimal one yourself and find it as early as possible.

The εε-greedy algorithm

By the law of large number, the optimal arm is the one with the highest expectation. Therefore, the goal is to pull again and again the arms with high expectation. The higher, the better.

Also by the law of large number, the expectation of an arm can be estimated with the sample mean. That is, the accumulated reward on one arm divided by the total count of pulls on that arm gives an excellent estimation of the expectation.

Denote q(a)q(a) as the expectation of the arm aa and Qt(a)Qt(a) as its estimation at time tt. We have Qt(a):=∑t−1i=1Ri⋅1Ai=a∑t−1i=11Ai=a,Qt(a):=∑i=1t−1Ri⋅1Ai=a∑i=1t−11Ai=a, where RiRi is the reward at time ii and AiAi is the arm pulled at time ii.

The greedy algorithm consists of pulling the arm with currently the highest estimation. That is, At:=argmaxaQt(a)At:=arg⁡maxaQt(a)

One problem with the greedy algorithm is that it is too rushy. If the optimal arm fails to behave well in its first pull, it will no longer be considered. (God knows how many girls missed their charming princes.)

Thus, Sutton advocates the εε-greedy algorithm, which has a probability of εε to deviate from the current best arm and pick an arm in random. In this way, the algorithm explores other arms, and the charming prince optimal arm may get a second chance.

Sutton’s experiment shows that the εε-greedy algorithms outperform the (pure) greedy algorithm, in both the average reward and the percentage of optimal arm pulled.

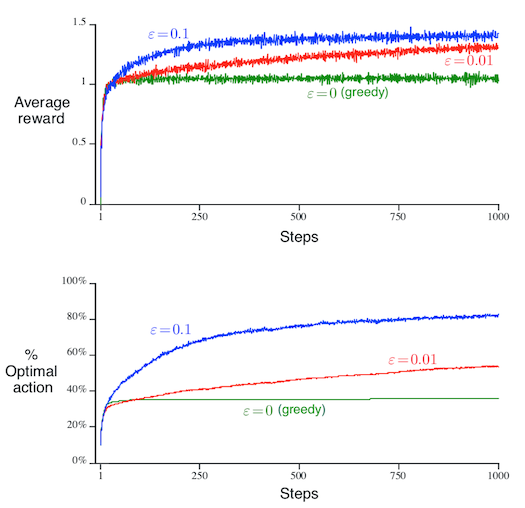
Later in this post, I will show you that Sutton’s conclusion is wrong. But before that, let me first introduce you to Sutton’s “clever” computational device.

Sutton’s efficient update of the estimation

The expectation of the estimation can be, naively, calculated from the accumulated reward and the count. Sutton, being a genius, would certainly avoid we commoners’ path and do something smart instead. Indeed, he updated the estimation from the past one in a recurrent manner: Qt=Qt−1+(Rt−Qt−1)/t.Qt=Qt−1+(Rt−Qt−1)/t. In this way, he saved the memory as well as accelerated the computation. Moreover, since the initial accumulated reward and count are both zero, the above formulation avoids the 0/0 error by manually setting the initial estimation.

Sutton picked zero for the initial estimation. He did not give the reason, but I can understand what he was thinking.

• Accumulated rewards start with zero, so it is natural to start the reward estimation with zero.
• The initial estimation serves as a prior just like in Bayesian statistics, so zero matches a zero-information prior just like the constant prior Bayesian statisticians would do.

The hidden parameter

Sutton launched the computation without a second thought, but let us analyze here the soundness of the above reasoning.

Q: Accumulated rewards start with zero, so it is natural to start the reward estimation with zero?

A: Both the accumulated reward and the count start with zero. Therefore, it is 0/0, which can be any number. Replacing an arbitrary number with zero does not sound right.

Q: Zero for the initial estimation matches a zero-information prior?

A: In Bayesian statistics, a constant prior does not give any privilege to any parameter value. However, it is true only for this parametrization. After a parameter transformation, a constant prior is no longer constant. Therefore, there is no real zero-information prior; every prior sneaks in some information. Similarly, assuming the initial estimation of expectation to be zero is just as informative as assuming it to be any other value.

In conclusion, the initial estimation is a parameter of the algorithm just like the parameter εε.

Sutton’s algorithm is one with two parameters instead of just one!

Tuning the initial estimation

All parameters can be tuned; so is the initial estimation. Here, I will give the experiment results generated with Zhang Shangtong’s code. I changed the initial estimation from 0 to 3 and -3.

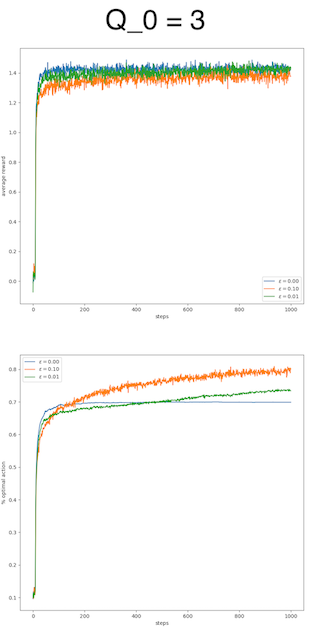
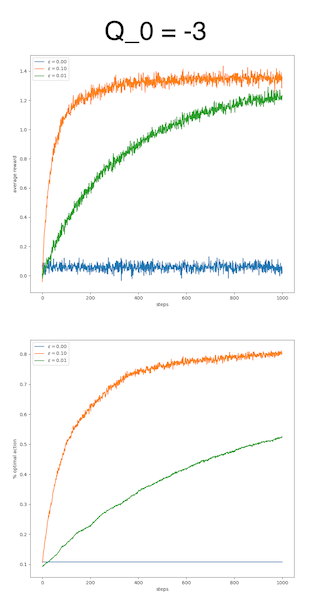
We can observe that the difference is huge by varying the initial estimation. For the value 3, the pure greedy algorithm works as well as the εε-greedy algorithms, if not better, in terms of average reward. For the value -3, the pure greedy algorithm just fails, whereas the εε-greedy algorithms adapt quite well.

This huge difference raises the question why the initial estimation plays such a critical role. To answer this question, it suffices to check the execution of the algorithm. In our experiment, the rewards are mainly located in [−5,5][−5,5], so a value of 3 is a quite decent reward and a value of -3 is quite poor. An optimistic initial estimation encourages the algorithm to explore, to look for better reward in this nourishing world. A poor initial estimation reflects a pessimistic mindset, which refrains the algorithm from exploring.

Surprisingly, the initial estimation itself is also a parameter reflecting the explore-exploit tradeoff, just like the εε. Moreover, it plays an upper hand. In this regard, the parameter εε is only secondary to the parameter initial estimation. The initial estimation explains the performance more than the εε does. A good initial estimation waives the necessity of εε.

Remove the hidden parameter

It is difficult to evaluate an algorithm with two parameters. With the interference of the initial estimation, we can hardly judge the effect of εε alone. To proceed, I propose to replace the subjective initial estimation with an objective one, namely by trying each arm once in the first place.

The following figure shows my experiment result. The legend items can be clicked to filter the curves. Although the pure greedy algorithm does not identify the optimal arm as often as the εε versions, it is still the best in terms of average reward. The explanation is that it can often find the second best arm, whereas the εε versions often waste their time in trying random (and bad) arms.

This result will not change even though the variance of the reward of each arm gets larger. The reason is that the motivation to find the absolute optimal arm is even weaker since chances play a more important role than choices do. The following figure shows the experiment result with a standard variation of 5.

The code to generate these plots can be found on my GitHub.

Conclusion

If the goal is to identify the optimal arm, then the εε-greedy versions win. If the goal is to gain high reward, then the pure greedy version is a safe bet.

Self-promotion time

This discovery would not be possible without my rigorous attitude toward programming. Just like I have always believed, rigorous and methodical programming can uncover truths and save the world.

In this regard, I might as well explain the advantages of my implementation over Zhang Shangtong’s.

• My implementation is truly object-oriented, whereas Shangtong’s uses an anti-pattern knowns as the God object.
• In my experiment, all algorithms are tested on a common set of 2000 bandits for fair comparison, whereas, in Shangtong’s experiment, each algorithm works on a different set of 2000 bandits.
• My implementation also provides an experiment where various algorithms work on the same bandit over and over instead of on 2000 independent bandits.
• My implementation allows the configuration of the standard variation of the reward.

For now, my repository is quite simple. I will probably add more items in the future depending on how soon I will find my next occupation. If you like my implementation, don’t hesitate to star and share it.