本文作者为张缔香，文章由 COS 编辑部审核发表，略有修改。点击此处下载 / 阅读本文 PDF 版本

R 软件做为一种统计软件，因其开源、免费、灵活的诸多优点得到越来越多的关注，无论网络上还是实体书店，关于 R 的教程铺天盖地，不甚枚举。因此，本文的目标不是做 R 的教程，而是将 R 和保险、精算教学结合起来，通过几个案例来说明 R 在保险、精算专业日常的教学和研究中可用之处。

作者在保险、精算的理论、专业知识方面水平有限，也没有编程基础，使用 R 也只 2 个月左右的时间，所以以下几个案例，无论在理论还是 R 编程技巧方面都有所欠缺。但做为加入 COS 的首篇文章，当求真求实，不做文抄公。

最后，本文的几个案例，均来自于作者在南开大学保险系读硕期间的一些课程作业，主要目的在于完成某一项任务，而没有过多地考虑通用性、用户界面友好性等，比如所有代码中几乎都没有写入报错、警告语句等。当然，作者也假定本文读者不单熟悉 R 的常用语法、函数等，而且具有相应的统计学、保险、精算专业知识，案例中的术语、结论等都直接引用，不做解释。

案例一 简单寿险产品的保费、准备金等

《南开大学经济学系列实验教材》丛书里有一本李秀芳老师主编《寿险精算实务实验教程》，是李秀芳老师 2010 年秋学期主讲的《寿险精算实务实验》课程的指定教材，作者也选修了这一门课。因此本案例主要来自这门课的实验内容，但在实现方法上，不再使用换算函数法，而转向概率的思路，利用精算等价原理来求得寿险产品的净保费、毛保费、准备金等。

本案例中的 R 脚本文件命名为 li.R，存放生命表的 CSV 文件命名为 clt03.csv。

1. 寿险计价函数 li()

描述：以列表的形式返回目标寿险产品的毛保费、理论责任准备金、费用。

参数：

• 投保人年龄 age：单个数值型，取值范围 0-105；
• 生存给付 bf.s：年初被保险人生存条件下的给付，非负数值型向量；
• 死亡给付 bf.d：被保险人死亡的年度末的给付，非负数值型向量；
• 定价利率 ir：按年计量的复利，数值型向量；
• 费用率 feerate：预定费用占毛保费的比例，非负数值型向量；
• 保费费率 prerate：均衡、递增、增减、或是其他形式的，数值型向量;
• 定价生命表 file：字符串型对象，存放生命表的. CSV 文件的文件路径；
• 产品类型 type：取值范围 {1、2、3、4}，分别对应男性、女养老金业务，男性、女性非养老金业务。

注释：

1. 生存给付、死亡给付的设置方式

以保额 1000 元，20 年定期死亡保险为例，那么死亡给付 bf.d=rep(1000,20)，生存给付bf.s=0；

若是保额 1000 元的 20 年定期年金，则 bf.d=0，bf.s=rep(1000,20)；

若保险给付不是有规律的序列，则必须以 c(x,y,…) 的形式具体地给出。

2. 费用率、保费费率的设置方式

费用率、保费费率必须设置为数值型向量，且长度必须与目标寿险产品的缴费期限相同。

以 10 年缴费为例，假定第一年的费用率 0.6，第二年 0.4，第三年 0.2，第四年及以后为 0.1，那么feerate=c(0.6,0.4,0.2,rep(0.1,7))。若费用率为 0，则必须指明为 0 ，不可省略。

同样以 10 年缴费为例，若是均衡保费，即每一年的保费都相同，则保费费率 prerate=rep(1,10)。递增型prerate=c(10:1)表示第一年缴 10 单位保费，第二年 9 单位，以此类推。

3. 生命表 CSV 文件的格式

生命表部分数据如下所示，存放在 CSV 文件里：

age	 male	    female      malep	     femalep
0	0.000722	0.000661	0.000627	0.000575
1	0.000603	0.000536	0.000525	0.000466
2	0.000499	0.000424	0.000434	0.000369
3	0.000416	0.000333	0.000362	0.00029
4	0.000358	0.000267	0.000311	0.000232
5	0.000323	0.000224	0.000281	0.000195

4. 本案例中采用的生命表的范围是 0 至 105 岁，所以在设置年龄、生存、死亡给付、费用率、保费费率时，年龄和其它四个参数长度最大者之和不能超过 106。

示例：

目标产品：20 岁投保、20 年死亡保险、定价利率 2.5%、10 年均衡缴费、男性非养老金业务的净保费

source(“li.R”)
li(age=20,bf.s=0,bf.d=rep(1000,20),ir=0.025,feerate=rep(0,10),prerate=rep(1,10),file="clt03.csv",type=1)

输出结果如下：

$premium
 [1] 1.623953 1.623953 1.623953 1.623953 1.623953 1.623953 1.623953
 [8] 1.623953 1.623953 1.623953

$reserve
 [1]  1.036481  2.059095  3.076657  4.096164  5.119730  6.148513
 [7]  7.183697  8.229508  9.282238 10.335088  9.710075  9.017654
[13]  8.244942  7.390757  6.447828  5.406646  4.256400  2.982906
[19]  1.569502  0.000000  0.000000  0.000000  0.000000  0.000000

$fee
 [1] 0 0 0 0 0 0 0 0 0 0

附录：附录一

2. 应用案例：

做为《寿险实务实验课程》的结课作业，作者设计了一款少儿保险产品，并用 R 和li()函数计算净保费、毛保费、现金价值、法定责任准备金、利润测试等，由于篇幅过大，待整理完毕之后再发上来。

案例二 BMS 奖罚系统

本案例的 R 脚本文件命名为 bms.R，索赔次数的 CSV 格式数据文件命名为 BMSclaim.csv。

1. 目标 BM 系统

本案例的目标 BMS 系统采用中国保险行业协会 2007 年 4 月制定的奖罚系统，具体如下所示：

表 1 中国保险行业协会制奖罚系统表 (2007.04)

规则 保费等级系数 等级 连续 3 年及 3 年以上无赔款 0.7 1 连续 2 年无赔款 0.8 2 上年无赔款 0.9 3 新保或上年发生 3 次以下赔款 1.0 4 上年发生 3 次赔款 1.1 5 上年发生 4 次赔款 1.2 6 上年发生 5 次及 5 次以上赔款 1.3 7

2. 转移概率矩阵

M=(1−∑4i=0pip4p3p1+p2p0001−∑4i=0pip4p3p1+p2p0001−∑4i=0pip4p3p1+p2p0001−∑4i=0pip4p3p1+p2p0001−∑4i=0pip4p3p1+p20p001−∑4i=0pip4p3p1+p200p01−∑4i=0pip4p3p1+p200p0)

其中pk=λkk!e−λ，表示投保人在一个保险年度中恰好发生 k 次索赔的概率。

3. 计算稳态分布

在稳定状态的处于各个级别的概率π=(π6,π7,…,π1)满足：

∑iπi=1, π=πM

π7=1−4∑0pi; π6=p4; π5=p3; π4=p2+p1; π3=p0−p20; π2=p20−p30; π1=p30

4. 利用索赔次数的实际数据求出具体的转移概率矩阵

本案例的索赔次数的观察值数据以如下所示，存放在 CSV 文件里。

laim	exposure
0	   27141
1	   5789
2	   1443
3	   457
4	   155
5	   56
6	   27
7	   2
8	   2
9	   1
10	   0

这里采用泊松逆高斯分布来拟合索赔次数分布，采用极大似然估计的方法来估计参数 (在做这个案例时，作者对 R 了解甚少，很多的功能、函数其实是可以在各种专业 package 里找到的，这里不详述。)。结果可通过以下的命令查看：

source("bms.R")
gamma_pig
beta_pig

按此估计的参数值，恰好发生 k 次索赔的概率可通过以下的命令查看：

print(pr)

按以上的索赔概率值，和事先设定好的转移规则，可得到转移概率矩阵，通过以下命令查看：

tmat

为求稳定状态下处于各保费等级的概率值，将转移矩阵取 30 次方 (实际上只需要 5 次方左右即可达到稳定的极限分布)，这个极限矩阵的各行已经趋于相同，也即所求的稳定状态下的保费等级分布。可能通过以下命令查看极限分布：

tmat_lim

5. 计算评价 BMS 系统优劣的指标

5.1 稳定状态下的平均保费率（新保费率为 1.0）

稳定状态下的平均保费率即是以稳定状态下处于各保费等级的概率分布为权重，各状态下的保费费率的加权平均值，计算结果为 0.8196。可以通过以下命令查看：

avp

5.2 相对稳定状态平均水平 (RSAL)

RSAL=(稳定平均水平 – 最低水平)/(最高水平 – 最低水平)=0.1993，可以通过以下命令查看：

rsal

5.3 对新司机的隐性惩罚 (ECL)

ECL=(新保费率 – 稳定平均费率)/ 稳定平均费率 = 0.2201，可以通过以下命令查看：

ecl

5.4 变异系数 COD = 标准差 / 均值

各年的平均保费以及变异系数可以通过以下命令查看：

cod_mat

平均保费和变异系数逐年变化曲线可以通过以下的命令查看：

graph1()

5.5 风险区分度

由于对索赔频率的数据采用的是泊松逆高斯拟合的，所以每个保费等级内不同保单的索赔频率服从参数为λ的泊松分布 (条件分布)；在所有保费等级中λ又服从逆高斯分布，其参数的极大似然估计已在前文交待。

对于各保费等级的保单，其索赔频率和均值和方差即为以上的复合分布的无条件均值和方差。均值和方差的计算均要计算无穷积分。在 R 里，采用离散化的方式来近似计算，即采取足够大的区间、足够小的间隔，通过求和的方式来计算无穷积分的近似值。各保费等级的内的索赔频率和方差的估计值以及相应结构 的参数可以通过以下命令来查看：

fin_mat

各个保费等级下的索赔频率曲线图可以通过以下的命令查看：

graph2()

5.6 BMS 的弹性

BMS 的弹性公式为：elac=(dp/p)/(dλ/λ)=dlnp/dlnλ，该公式为连续形式下的弹性公式，在实验中稳定状态下平均保费的函数形式的精确表达式难以计算出，只能采取离散化的方式来近期计算。具体思路就是把微分用差分代替，取间隔够小、数量够多的λ及对应的稳定状态下的平均保费，得到弹性的曲线图。可以通过以下的命令查看：

graph3()

代码：附录二

案例三 利用 LeeCarter 模型进行死亡率预测

本案例中的脚本文件命名为 forecast.R，两个 CSV 文件分别命名为 93pm.csv 和 03pm.csv。

1. 数据来源及初步整理

选用中国生命表 90-93 养老金男表和 00-03 养老金男表做为本案例的基础数据。把 101 至 105 岁划分为一组，100 岁及其以上每一整数年龄分为一组，共 102 组。100 岁及其以上组死亡率直接采用死亡率 qx，100 岁以上组采用中心死亡率。采用线性插值法得出 1994-2002 年间的死亡率。90-93 养老金男表和 00-03 养老金男表各存放于一个 CSV 文件中，按如下图所示的格式存放数据：

在 R 的命令窗口输入以下命令来观察 1993-2003 死亡率矩阵：

source(“forecast.R”)
tab9303

把死亡率取自然对数，然后减去每一年龄的死亡率的对数在 1993-2003 年间的均值，得到残差矩阵 A。在 R 的命令窗口输入以下命令来观察均值和 A：

ax
amat

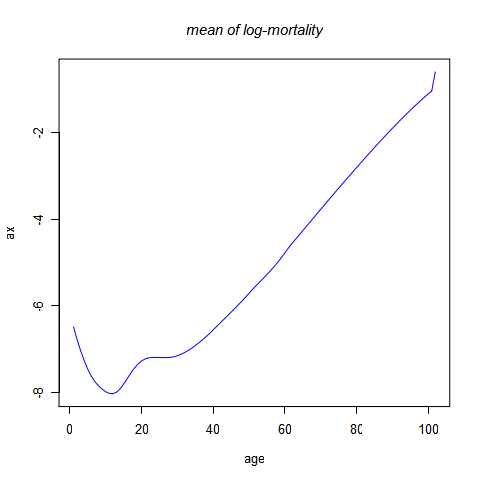
各年龄的均值如上图所示。

2. SVD 分解

2.1 k 值

利用 R 里的svd()命令对死亡率的残差矩阵 A 做 SVD 分解。通过以下命令可观察分解得出的 U、S、V 矩阵：

svda$u
svda$d
svda$v

把 S 矩阵右乘 V 的转置矩阵，取其结果的第一行，即为 Lee-Carter 模型中的 kt。按 1993-2003 的顺序，kt 的各个值如下：

-2.2891315， -1.9135574， -1.5181148， -1.1002924， -0.6570094，-0.1844099，

0.3224553， 0.8701444， 1.4677250， 2.1284910， 2.8736996

可以在 R 里输入以下命令观察 kt 的值及其总和：

kt
sum(kt)

2.2 b 值

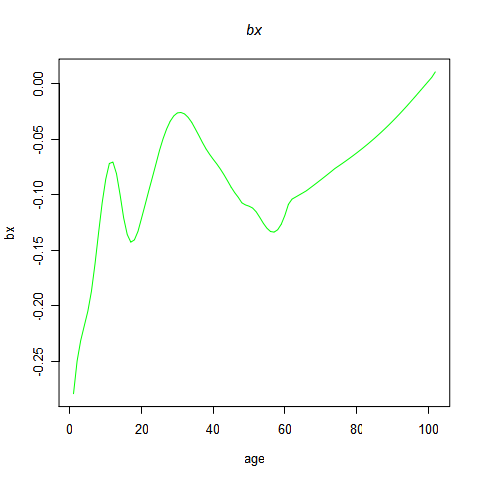
在 SVD 分解得出的 U 矩阵里，取其第一列，即可得到未经中心化的 bx 的值。本人采用保险研究增刊里的方法，采用线性拟合的方法来求 bx 的值。在 R 里输入以下命令可观察 bx 的拟合值以及拟合结果：

bmat

在 bmat 矩阵中其中，如各列名称所示，第一列为年龄，第二列为 bx，第三至六列分别为线性拟合 bx 时的 t 值、t 临界值、F 值、F 临界值和拟合优度值，可以看出所有的 bx 都是显著的。

2.3 k 值的调整

采用最小化 RMSPE 的方法来得到最优的 kt 值，RMSPE 的公式如下：

采用非线性最小值的算法来求解使得 RMSPE 最小的 kt 值，具体如下：

-2.3445627， -1.9458174， -1.5271026， -1.0869498， -0.6237423， -0.1356942

0.3791744， 0.9230672， 1.4984474， 2.1080823， 2.7550978

通过如下命令来观察求出的 k 值：

kt_adj

2.4 预测

对 kt 值和时间变量 1-11(1993 年做为 1，2003 做为 11，或者直接用 1993，1994，……2003 区别只在系数的值，对预测没有影响)，得出 kt 的向后 15 期的预测值如下：

3.044373， 3.551768， 4.059164， 4.566559， 5.073955， 5.581350， 6.088746， 6.596141， 7.103537， 7.610932， 8.118328， 8.625723， 9.133118， 9.640514， 10.147909

可以通过如下命令查看 kt 的 15 期预测值及其 95% 置信区间：

k.lm

使用以上的 kt 预测值来预测后 15 年的出生平均余命，

80.95256 ，81.35479 ，81.74651 ，82.12812， 82.49997 ，82.86240， 83.21572，83.56023，

83.89621， 84.22392 ，84.54362， 84.85554， 85.15991， 85.45694， 85.74685

下图为向后预测 39 期得出的出生平均余命的预测值，在 2050 年左右，中国男性的平均出生余命达到 90 岁。这似乎有些过高，所以本模型只适合做 15 年以内的预测。

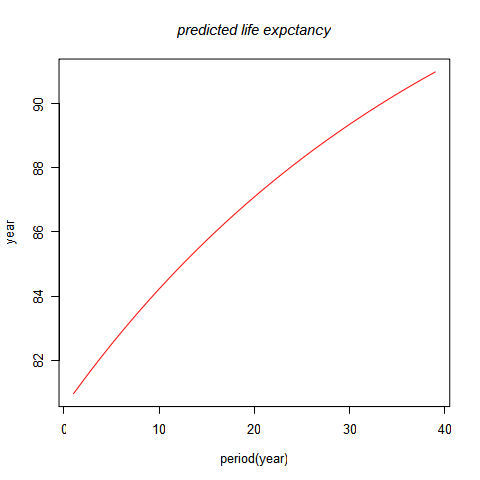
代码：附录三

R 软件在精算教学中的应用案例（附录）（包含附录一、二、三）

敬告各位友媒，如需转载，请与统计之都小编联系（直接留言或发至邮箱：[email protected]），获准转载的请在显著位置注明作者和出处（转载自：统计之都），并在文章结尾处附上统计之都微信二维码。

← 统计学论文的发表流程、及统计学家的晋升和合作（内幕） Sweave 后传：统计报告中的大规模计算与缓存 →

发表 / 查看评论