奔驰定理与重心坐标

1. 奔驰定理

在讲平面向量的时候，遇到了一个经典的题目：

证明如下：如图，延长 APAPAP 交 BCBCBC 于 点 QQQ，则 S△PBCS△PCA+S△PAB=∣PQ∣∣AP∣\dfrac{S_{\triangle PBC}}{S_{\triangle PCA} + S_{\triangle PAB}} = \dfrac{|PQ|}{|AP|}S△PCA​+S△PAB​S△PBC​​=∣AP∣∣PQ∣​，

故 PQ→=−S△PBCS△PCA+S△PAB⋅PA→\overrightarrow{PQ} = - \dfrac{S_{\triangle PBC}}{S_{\triangle PCA} + S_{\triangle PAB}} \cdot \overrightarrow{PA}PQ​=−S△PCA​+S△PAB​S△PBC​​⋅PA．

另外，因为 ∣BQ∣:∣QC∣=S△PAB:S△PCA|BQ|:|QC| = S_{\triangle PAB} : S_{\triangle PCA}∣BQ∣:∣QC∣=S△PAB​:S△PCA​，所以 PQ→=S△PCA⋅PB→+S△PAB⋅PC→S△PCA+S△PAB \overrightarrow{PQ} = \dfrac{S_{\triangle PCA} \cdot \overrightarrow{PB} + S_{\triangle PAB} \cdot \overrightarrow{PC}}{S_{\triangle PCA} + S_{\triangle PAB}}PQ​=S△PCA​+S△PAB​S△PCA​⋅PB+S△PAB​⋅PC​，

故 −S△PBC⋅PA→=S△PCA⋅PB→+S△PAB⋅PC→- S_{\triangle PBC} \cdot \overrightarrow{PA} = S_{\triangle PCA} \cdot \overrightarrow{PB} + S_{\triangle PAB} \cdot \overrightarrow{PC}−S△PBC​⋅PA=S△PCA​⋅PB+S△PAB​⋅PC，移项后命题得证．

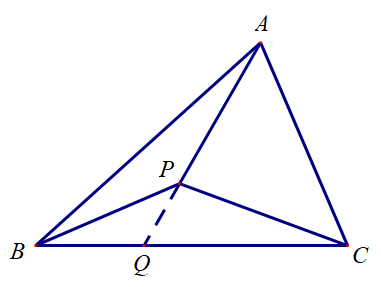
这个结论因为它的图形长得像奔驰的标志，被称为 “奔驰定理”．

这个名字最早的出处不详，但实际上，这对应的就是三角形的 “重心坐标”．

2. 三角形的重心坐标

显然，重心坐标并不是唯一的，(kλ0:kλ1:kλ2)( k \lambda_0 : k \lambda_1 : k \lambda_2 )(kλ0​:kλ1​:kλ2​) 也是点 PPP 相对于 △ABC\triangle ABC△ABC 的重心坐标．

为了保证唯一性，我们可以进行对其正规化，取 λi′=λi/∑k=02λk\lambda_i^\prime = \lambda_i / \displaystyle\sum_{k=0}^2 \lambda_kλi′​=λi​/k=0∑2​λk​ ，则 ∑i=02λi′=1\displaystyle\sum_{i=0}^2 \lambda_i^\prime = 1i=0∑2​λi′​=1，此时称 (λ0′:λ1′:λ2′)(\lambda_0^\prime : \lambda_1^\prime : \lambda_2^\prime)(λ0′​:λ1′​:λ2′​) 为其正规化（重心）坐标．

2.1. 重心坐标的存在性

对 △ABC\triangle ABC△ABC 所在平面内任意一点 PPP，根据平面向量基本定理，存在唯一的实数对 (λ,μ)(\lambda, \mu)(λ,μ)，使得 AP→=λAB→+μAC→\overrightarrow{AP} = \lambda \overrightarrow{AB} + \mu \overrightarrow{AC}AP=λAB+μAC．因此

OP→=OA→+AP→=OA→+λAB→+μAC→=OA→+λ(OB→−OA→)+λ(OC→−OA→)=(1−λ−μ)OA→+λOB→+μOC→\begin{aligned} \overrightarrow{OP} &= \overrightarrow{OA} + \overrightarrow{AP} \\ &= \overrightarrow{OA} + \lambda \overrightarrow{AB} + \mu \overrightarrow{AC} \\ &= \overrightarrow{OA} + \lambda \left( \overrightarrow{OB} - \overrightarrow{OA} \right) + \lambda \left( \overrightarrow{OC} - \overrightarrow{OA} \right) \\ &= (1-\lambda-\mu)\overrightarrow{OA} + \lambda\overrightarrow{OB} + \mu\overrightarrow{OC} \end{aligned} OP​=OA+AP=OA+λAB+μAC=OA+λ(OB−OA)+λ(OC−OA)=(1−λ−μ)OA+λOB+μOC​

取 (λ0,λ1,λ2)=(1−λ−μ,λ,μ)( \lambda_0, \lambda_1, \lambda_2 ) = (1-\lambda-\mu,\lambda,\mu)(λ0​,λ1​,λ2​)=(1−λ−μ,λ,μ) 即可．注意这已经是正规化坐标．

2.2. 正规化坐标的符号

当点 PPP 位于 △ABC\triangle ABC△ABC 内部的时候，λ,μ,λ+μ∈(0,1)\lambda, \mu, \lambda+\mu \in (0,1)λ,μ,λ+μ∈(0,1)，故 1−λ−μ∈(0,1)1-\lambda-\mu \in (0,1)1−λ−μ∈(0,1)，也就是三项均是正数．

对于 △ABC\triangle ABC△ABC 外的情况，可以参考下图：

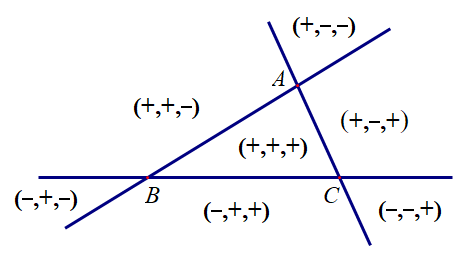
2.3. 重心坐标的几何意义

在平面直角坐标系 xOyxOyxOy 中，设 A(x1,y1)A(x_1,y_1)A(x1​,y1​)，B(x2,y2)B(x_2,y_2)B(x2​,y2​)，C(x3,y3)C(x_3,y_3)C(x3​,y3​)，P(xP,yP)P(x_P,y_P)P(xP​,yP​)，点 PPP 相对于 △ABC\triangle ABC△ABC 的重心坐标为 (α:β:γ)(\alpha:\beta:\gamma)(α:β:γ)，其中 α+β+γ=1\alpha+\beta+\gamma=1α+β+γ=1．

根据定义，OP→=αOA→+βOB→+γOC→\overrightarrow{OP} = \alpha\overrightarrow{OA} + \beta\overrightarrow{OB} + \gamma\overrightarrow{OC}OP=αOA+βOB+γOC，
因此

{xP=αx1+βx2+γx3yp=αy1+βy2+γy31=α+β+γ⟺(xPyP1)=(x1x2x3y1y2y3111)(αβγ)\left\{ \begin{aligned} x_P &= \alpha x_1 + \beta x_2 + \gamma x_3 \\ y_p &= \alpha y_1 + \beta y_2 + \gamma y_3 \\ 1 &= \alpha + \beta + \gamma \end{aligned} \right. \Longleftrightarrow \begin{pmatrix} x_P \\ y_P \\ 1 \end{pmatrix} = \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \\ \gamma \end{pmatrix} ⎩⎪⎪⎨⎪⎪⎧​xP​yp​1​=αx1​+βx2​+γx3​=αy1​+βy2​+γy3​=α+β+γ​⟺⎝⎛​xP​yP​1​⎠⎞​=⎝⎛​x1​y1​1​x2​y2​1​x3​y3​1​⎠⎞​⎝⎛​αβγ​⎠⎞​

根据 Cramer 法则，

α=S△PBCS△ABC,β=S△PCAS△ABC,γ=S△PABS△ABC\alpha = \frac{S_{\triangle PBC}}{S_{\triangle ABC}},\quad \beta = \frac{S_{\triangle PCA}}{S_{\triangle ABC}},\quad \gamma = \frac{S_{\triangle PAB}}{S_{\triangle ABC}} α=S△ABC​S△PBC​​,β=S△ABC​S△PCA​​,γ=S△ABC​S△PAB​​

这里的面积指的是三角形的有向面积，正负与三个点的位置关系有关．

所以，(S△PBC:S△PCA:S△PAB)(S_{\triangle PBC}:S_{\triangle PCA}:S_{\triangle PAB})(S△PBC​:S△PCA​:S△PAB​) 就是点 PPP 相对于 △ABC\triangle ABC△ABC 的重心坐标，这对应的就是 “奔驰定理” 中的三个系数．

实际上，根据 “奔驰定理”，

S△PBC⋅(OA→−OP→)+S△PCA⋅(OB→−OP→)+S△PAB⋅(OC→−OP→)=0S_{\triangle PBC} \cdot \left(\overrightarrow{OA} - \overrightarrow{OP}\right) + S_{\triangle PCA} \cdot \left(\overrightarrow{OB} - \overrightarrow{OP}\right) + S_{\triangle PAB} \cdot \left(\overrightarrow{OC} - \overrightarrow{OP}\right) = \mathbf{0} S△PBC​⋅(OA−OP)+S△PCA​⋅(OB−OP)+S△PAB​⋅(OC−OP)=0

(S△PBC+S△PCA+S△PAB)⋅OP→=S△PBC⋅OA→+S△PCA⋅OB→+S△PAB⋅OC→\left(S_{\triangle PBC} + S_{\triangle PCA} + S_{\triangle PAB}\right) \cdot \overrightarrow{OP} = S_{\triangle PBC} \cdot \overrightarrow{OA} + S_{\triangle PCA} \cdot \overrightarrow{OB} + S_{\triangle PAB} \cdot \overrightarrow{OC} (S△PBC​+S△PCA​+S△PAB​)⋅OP=S△PBC​⋅OA+S△PCA​⋅OB+S△PAB​⋅OC

也可以直接得到，当点 PPP 在 △ABC\triangle ABC△ABC 内部的时候，它相对于 △ABC\triangle ABC△ABC 的重心坐标为 (S△PBC:S△PCA:S△PAB)(S_{\triangle PBC}:S_{\triangle PCA}:S_{\triangle PAB})(S△PBC​:S△PCA​:S△PAB​)．

由于三角形的重心坐标和面积有关系，因此也被称为面积坐标．

2.4. 重心坐标名称的来源

考虑平面内三个质点 AAA、BBB、CCC，它们的质量分别为 m1m_1m1​、m2m_2m2​、m3m_3m3​，则该质心系的质心相对于 △ABC\triangle ABC△ABC 的重心坐标恰好为 (m1,m2,m3)(m_1,m_2,m_3)(m1​,m2​,m3​)．

3. 三角形各中心的重心坐标

下表列出了几个常见的三角形中心的重心坐标．

其它特殊点的重心坐标，可以查看 ETC，里面每个点下面列出的 Barycentrics 就是该点的重心坐标．

4. 重心坐标的一般定义

事实上，重心坐标的定义可以推广到 nnn 维向量空间，甚至是仿射空间．

考虑 nnn 维仿射空间 A\mathbf AA 中的仿射无关的 n+1n+1n+1 个点 A0,A1,⋯,AnA_0,A_1,\cdots,A_nA0​,A1​,⋯,An​，即 A0,A1,⋯,AnA_0,A_1,\cdots,A_nA0​,A1​,⋯,An​ 是一个 nnn 维单形的顶点，则对于任意一点 P∈AP \in \mathbf AP∈A，存在不全为零的实数 λ0,λ1,⋯,λn\lambda_0,\lambda_1,\cdots,\lambda_nλ0​,λ1​,⋯,λn​，使得

(λ0+λ1+⋯+λn)OP→=λ0OA1→+λ1OA2→+⋯+λnOAn→(\lambda_0+\lambda_1+\cdots+\lambda_n)\overrightarrow{OP} = \lambda_0\overrightarrow{OA_1}+\lambda_1\overrightarrow{OA_2}+\cdots+\lambda_n\overrightarrow{OA_n} (λ0​+λ1​+⋯+λn​)OP=λ0​OA1​​+λ1​OA2​​+⋯+λn​OAn​​

对于任意一点 OOO 成立，则称 (λ0:λ1:⋯:λn)(\lambda_0:\lambda_1:\cdots:\lambda_n)(λ0​:λ1​:⋯:λn​) 为点 PPP 相对于 A0,A1,⋯,AnA_0,A_1,\cdots,A_nA0​,A1​,⋯,An​ 的重心坐标．

重心坐标是一种齐次坐标，在仿射变换下保持不变．

(λ0:λ1:⋯:λn)(\lambda_0:\lambda_1:\cdots:\lambda_n)(λ0​:λ1​:⋯:λn​) 和 (μ0:μ1:⋯:μn)(\mu_0:\mu_1:\cdots:\mu_n)(μ0​:μ1​:⋯:μn​) 都是点 PPP 相对于 A0,A1,⋯,AnA_0,A_1,\cdots,A_nA0​,A1​,⋯,An​ 的重心坐标的充要条件是，存在非零常数 kkk，使得对于任意的 iii，有 λi=kμi\lambda_i = k\mu_iλi​=kμi​．

类似的，也可以对其进行正规化，取 ∑i=0nλi=1\displaystyle\sum_{i=0}^n \lambda_i=1i=0∑n​λi​=1 即可．