探索性因子分析

在之前的章节中，我们讨论了主成分分析——一种多元数据降维以及理解变量间关联模式的方法。 在这个章节中，我们讨论，这是一种类似的方法， 基于一种不同的隐含的模型，被称作””。 虽然这两种方法比较类似，但探索性因子分析经常被用于完成和主成分分析相同的目标。 我们这里的目的是强调他们之间概念上的区别。 公因子模型关于数据集中的每个变量是如何计量的有明确的假设。 模型认为每次计量的变化是由几个相对较少的共同因子造成的（即两个或多个变量之间不可观测的共同特性）。 尽管一个变量实际上可能有一个或多个特性因子，统计上不可能将这些特殊变量混淆。 探索性因子分析的目标是发现共同因子（区别于特性因子）并解释它们和观测数据之间的关系。 因此，尽管用于完成探索性因子分析的解决方案和主成分分析类似，但他们背后的模型是不相同的。

在探索性因子分析中，我们让观测到的数据间关联模式决定因子构成。 在《验证性因子分析》中，我们转向验证性数据分析， 利用一些关于因子构成的先验知识，去检验他们是否与数据一致。 在验证性数据分析中，背后的模型与探索性因子分析是相同的，但是求解过程则大不相同。

公因子模型提供了一个明确的框架让我们可以对数据计量属性进行评估。 在这个章节提供的案例中，我们假设特性因子的变化可以单纯地由计量误差解释。 广义地，为了区分特性方差（即特性因子的方差）和误差方差（即每个变量计量误差的方差），计量可靠性的独立评估是很必要的。 如果没有这种独立评估，我们就假设特性因子方差反映了计量误差。 这让我们对计量的可靠性有了一定的了解：误差方差越小，计量越可靠。 《验证性因子分析》中有关于可靠性的形式化概念。

在这章节的编写过程中，我们特别注重使用旋转来提高因子分析解的解释性。 因为探索性因子分析的方向是随意的，有时候选择有简单结构的解才是有意义的 （即在某种意义上最易于解释的一种，由 Thurstone 在1947年提出）。 实际上，在对数据进行主成分分析时旋转也同样可行。 这里所介绍的所有旋转方法都可以应用于主成分分析。

探索性因子分析与大多数主成分分析的应用场景相同；而公因子模型当测量模型的明确假设是适当时更合适。 下面介绍探索性因子分析的两种说明性应用：分析”潜在特征”或”不可观测的特性”、使用因子得分分析依赖性。

分析”潜在特征”或”不可观测的特性”

有的时候区分数据变量和它被设计用于计量的概念是非常重要的。 在处理物理特性时，例如长度和重量（测量仪器具有高精度），这种区分是不必要的，因为目标属性几乎可以被完美计量。 但是，当处理态度、信仰、感知以及其他心理学特性时，我们的计量方法是不完美的。

在市场，调查研究员可能对获取某个概念（例如”顾客满意度”）的信息感兴趣，以更好理解这个概念以及企业行为对它的影响。 设计一个单一的调查问题来准确认知如”顾客满意度”这种概念，即使是可能的，也非常困难。 相反的，研究者可能回设计一个包含几个问题的调查问卷，每个问题并不能完美反映”顾客满意度”，但能够反应某一个方面。 使用因子分析，可以找到这些问题背后的共同变量（很可能反映了客户潜在的满意度）并分离出计量中的非系统误差。 从公因子模型中得到的因子得分可以作为后续分析和建模中顾客满意度的一个指数（或多个指数，取决于潜在变量的个数）。

Aaker（1997）使用探索性因子分析研究了品牌特性的几个维度。 为了处理 114 个特性指标（从心理学和市场调研研究中产生的 309 个候选指标中筛选得到的）， Aaker 让受访者对一组10个品牌中的每一个进行 114 个特性指标的 5 级尺度打分（从 1 到 5 ，1 代表完全没有体现，5 代表非常能够体现）。 她使用了四个不同的品牌数据集，每组都有一个焦点品牌（李维斯牛仔）和九个其他的 （都是非常突出的、广为人知的国民品牌，涵盖了多个不同的产品类型），一共 37 个不同的品牌。 Aaker 对打分结果按人数平均（每个品牌在每个指标上都被大约 150 到 160 个受访者打分，除了李维斯被所有人打分） 并对指标间 $114 \times 114$ 维的相关矩阵进行了因子分析。

Aaker 选择了一个五个因子的解，解释了 90% 的指标差异。 在进行了旋转之后，她将这些因子标记为： 诚意（sincerity，解释了 26.5% 的差异）、刺激（excitement，25.1%）、竞争力（competence，17.5%）、 世故（sophistication，11.9%）和粗犷（ruggedness，8.8%）。 表展示了这五个因子的一些最高度相关的指标。 基于这个研究的结果， Aaker 继续构造并验证了 42 项测度用于测量者五个品牌特性的成分。

SincerityExcitementCompetenceSophisticationRuggednessHonestDaringReliableGlamorousToughGenuineSpiritedResponsiblePretentiousStrongCheerfulImaginativeDependableCharmingOutdoorsyDown-to-earthUp-to-dateEfficientRomanticMasculineFriendlyCoolIntelligentUpper classSuccessfulSmooth

使用因子得分分析依赖性

和主成分分析一样，减少维数往往是因子分析的主要目标。 一方面，这么做有助于对数据进行可视化；另一方面，也有助于增加模型简洁性。 例如，在一个关于新的豪华车概念的大型市场调研中，Roberts（1984）调查了 162 个目标消费者关于他们在汽车的认知。 他使用九个维度来计量他们在熟悉的汽车模型的认值：奢华、样式、可靠性、油耗、安全、维修成本、质量、续航以及道路偏好。 他的最终目标是建立一个模型，将认知和偏好联系起来；但是可用于拟合这个模型的自由维度数太有限。 因此他使用因子分析来看看他是否可以找到一组更少数目的潜在公因子可以替代。

Roberts 发现一个双因子解解释了这九个特性中 60% 的差异。Roberts 然后旋转了解（使用方差最大法）来使得它更容易解释。 指标和因子之间的相关系数被称为， 如下表所示；相关系数最高的是用下划线标出。 这种模式指示第一个因子（与奢华、样式、安全性、道路偏好等指标高度相关）反映了车的情感诉求， 而第二个指标（与可靠性、油耗、维修成本、质量和续航相关）反映了车的经济性。 Roberts 将这两个因子标记为吸引力和合理性。

AppealingSensibleLuxury0.884-0.051Style0.7480.153Reliability0.3960.691Fuel Economy-0.2020.786Safety0.7200.172Maintenance0.1490.756Quality0.5010.650Durable0.3860.677Performance0.6860.391

使用这个模型， Roberts 计算每个被打分的车模在每个因子得分的平均值，然后使用这些因子得分来回归前面所述的受访者喜好。 使用这两个因子，他能够解释 30% 的受访者喜好的差异（依据调整 ）；这两个因子都高度显著。 相反，当 Roberts 使用 9 个指标来回归受访者喜好时，拟合数据的能力仅有轻微的提高（调整 是 33%）， 而他参数估计值的标准差大幅增加，由于指标间的多重共线性（实际上，九个系数中只有两个在 0.05 等级下显著）。 使用这个简洁的因子模型， Roberts 能够评估新概念车的相对定位，并精确预测市场价值。

和主成分分析一样，对因子分析的直观感觉也最好是通过一个简单的例子进行。 考虑 Holzinger 和 Swineford 进行的针对儿童的心理学考试（1939）。 他们对七、八年级的儿童进行了一些不同的考试。 为了使问题简化，我们主要关注下面五个考试： 篇章理解（$PARA$）、句子完成（$SENT$）、单词含义（$WORD$）、加法（$ADD$）、数点（$DOTS$）。 我们使用变量 $X_1$到 $X_5$表示这五个不同的考试。 他们间的相关系数（基于 145 个儿童组成的样本）如下表所示。

$PARA$$SENT$$WORD$$ADD$$DOTS$$PARA$$1.000$$SENT$$0.722$$1.000$$WORD$$0.714$$0.685$$1.000$$ADD $$0.203$$0.246$$0.170$$1.000$$DOTS$$0.095$$0.181$$0.113$$0.585$$1.000$

在因子分析中，我们假设考试得分可以用一个潜在公因子和几个特殊因子（每个考试一个特殊因子）的函数来描述。 也就是说，例如，我们相信这些学生的考试得分背后都有一个公因子，记为 $\xi$ 。 这个因子可能反映了每个学生的智力或应试能力。 我们的但因子模型表示，对考试 $i$的得分 $X_i$是因子 $\xi$ （对所有五个考试来说都是相同的） 和考试 $i$的特有的因子——不妨记为 $\delta_i$——的函数。 在很多可以用于估计公因子模型参数的方法中，所有我们实际可以估计的是唯一方差（或称”唯一性”），即这个特殊因子和测量误差方差的和。 我们假设这个特殊因子方差完全由测量误差引起，反映考试在完美捕获背后共同因子能力的不足。 由于特殊因子仅影响他们特别针对的计量（即 $\delta_i$仅影响考试 $i$）， 我们的后续处理将在假设这些特殊因子 $\delta$互不相关 （即对于所有不同 [^1] 的 $i$和 $j$，$\delta_i$和 $\delta_j$之间的相关系数是 0）。 且与潜在的公因子 $\xi$也不相关的假设下进行。 这些都是公因子模型的标准假设。

这个单因子模型可以用图中的示意图所表示。

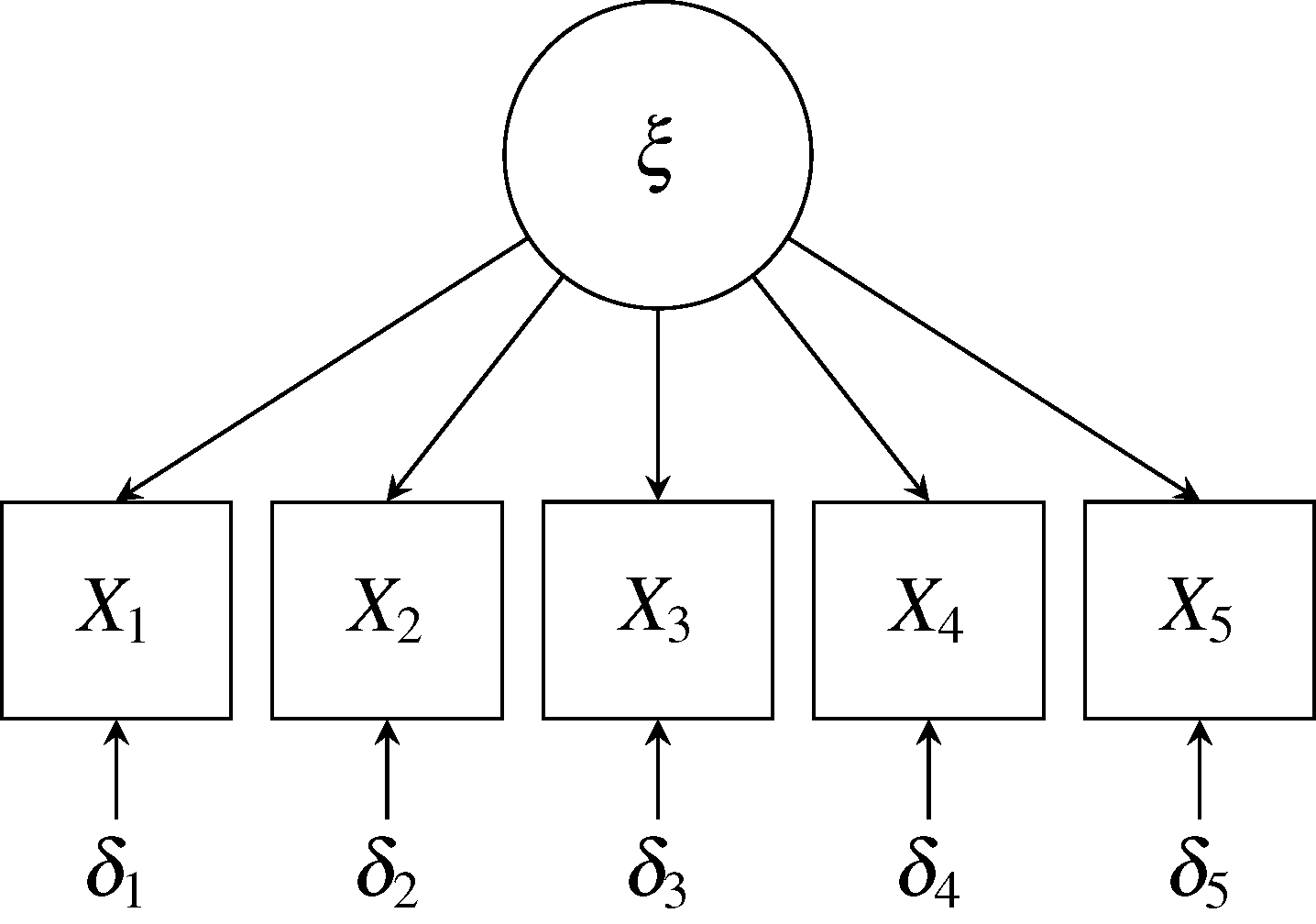
图中指向每个考试变量的箭头（即观测计量值，用盒形表示）指示测量中变异的贡献源。 这种情况下，每个测量值 $X_i$有两个变异的贡献源（都不可观测）：公因子 $\xi$和一个特殊因子 $\delta_i$。 用公式的形式，可以写作下式 $$\begin{aligned} X_1 & = \lambda_1\xi + \delta_1 \ X_2 & = \lambda_2\xi + \delta_2 \ X_3 & = \lambda_3\xi + \delta_3 \ X_4 & = \lambda_4\xi + \delta_4 \ X_5 & = \lambda_5\xi + \delta_5 \ \end{aligned}$$ 在这些公式中，系数 $\lambda$ 反映了潜在公因子 $\xi$体现在测量值 $X$中的程度。 假设 $X$和 $\xi$ 都是标准化的变量（即有零均值和单位方差）， $X_i$的方差可以被分解为： $$\mathrm{var}{X_i} = \mathrm{var}{\lambda_i\xi + \delta_i} = \lambda_i^2 + \mathrm{var}{\delta_i} = 1$$ 由于变量被标准化，$\lambda_i$可以解释为相关系数。 $\lambda_i^2$ 可被解释为 $X_i$中的变化在公因子 $\xi$反映的比例，被称作 $X_i$的。 $X_i$中剩余的变化可由特殊因子 $\delta_i$解释。 如果用 $\theta_{ii} = \mathrm{var}{\delta_i}$来表示特殊因子的方差（我们假设它反映了 $X_i$的计量误差）， 那么 $X_i$的共同度等于 $$1 - \theta_{ii}^2$$

如果 $X_i$的共同度接近 1 （即误差方差接近 0），表示 $X_i$是潜在公因子 $\xi$的一个几乎完美的度量。 反之，如果共同度接近 0，表示 $\xi$ 完全没有体现在 $X_i$中 （如果 $X_i$ 是一个对学生智力设计较差的考试，这种情况就可能发生）， 那么系数 $\lambda$可能接近零，并且几乎 $X_i$的所有方差都由特殊因子 $\delta_i$ 解释。

在这个特殊的示例中， 我们从一个潜在于 Holzinger 和 Swineford 的研究中考试得分的单共同因子假设开始（一种类似于通用智力的东西）。 但是，也有一种情况，即考试中的个人表现可能是多于一个潜在能力的函数。 例如，我们可能认为学生的考试表现有两个不同的内在能力所决定—— 文学天赋（记为 $\xi_1$）和计量天赋（记为 $\xi_2$）—— 并且这两种不同的因子在不同类型的考试中有不同程度的表现。 这个双因子模型如图所示。

在双因子模型中，在每个考试得分度量 $X_i$中有三个源贡献了变异： 两个公因子 $\xi_1$和 $\xi_2$以及一个特殊变量 $\delta_i$。 使用公式的形式，双因子模型可以写作： $$\begin{aligned} X_1 & = \lambda_{11}\xi_1 + \lambda_{12}\xi_2 + \delta_1 \ X_2 & = \lambda_{21}\xi_1 + \lambda_{22}\xi_2 + \delta_2 \ X_3 & = \lambda_{31}\xi_1 + \lambda_{32}\xi_2 + \delta_3 \ X_4 & = \lambda_{41}\xi_1 + \lambda_{42}\xi_2 + \delta_4 \ X_5 & = \lambda_{51}\xi_1 + \lambda_{52}\xi_2 + \delta_5 \ \end{aligned}$$

如前，系数 $\lambda$反映了潜在公因子 $\xi$体现在测量值 $X$中的程度。 如果 $X$和 $\xi$被标准化，参数 $\lambda$可以被解释为相关系数。 如果我们进一步假设潜在因子互不相关（公因子模型的另一个标准假设）， 那么每个考试度量的共同度由那个变量因子载荷的平方和给出； 因此，$X_i$ 的共同度由 $\lambda_{11}^2 + \lambda_{12}^2$给出。

考虑在双因子模型下，如果一个学生有较高的文学天赋（高 $\xi_1$）和较低的计量天赋（低 $\xi_2$），那会发生什么。 我们可以预期这个学生在那些比计量天赋更需要文学天赋的考试中表现良好。 如果学生在句子完成考试中的表现只依赖于他（她）的文学天赋，那么我们应该期望一个 接近于 1 的 $\lambda_{11}$的值和一个接近于 0 的 $\lambda_{12}$的值。

在没有较强的关于学生考试表现潜在因子结构的先验知识这个探索性设定中， 我们希望能够从数据中能够推到出潜在因子的合理数量以及公因子模型公式中的系数值。 这个方法（在下一节中会详细阐述）和主成分分析的方法相类似，都是尝试提取一个较少数量的因子组以充分代表观测值的相关矩阵。 不同的是，公因子模型中，我们必须解释特殊因子 $\delta$ ，而这没有在主成分分析中体现。

和主成分分析一样，探索性因子分析的求解过程主要关注于 $\mathbf{X}$ 的协方差矩阵或相关系数矩阵的分解。 这两种方法的不同之处在于，特殊因子是公因子模型的一部分。 由于这些特殊因子被认为彼此不相关，而且与潜在公因子独立，这些因子仅仅贡献于协方差矩阵的对角线元素。 这一点通过检查每个度量值 $X_i$协方差矩阵的对角线元素可以很容易发现： $$\mathrm{var}{X_i} = \mathrm{var}{\lambda_{i1}\xi_1 + \lambda_{i2}\xi_2 + \delta_i}$$

$X_i$方差表达式中有九个交叉项。 根据公因子模型加入的独立性假设（以及进一步的公因子被标准化为具有单位方差的假设）， 所有的协方差项都排除在模型之外，只剩 $$\mathrm{var}{X_i} = \lambda_{i1}^2 + \lambda_{i2}^2 + \theta_{ii}^2$$ 其中 $\theta_{ii}^2 = \mathrm{var}{\delta_i}$。 因此，特殊因子出现在 $\mathbf{X}$ 的协方差矩阵中的唯一位置就是对角线，也就是他们对每个度量贡献变异的地方。

如果我们实现直到每个特殊因子的变异呢？ 如果这样，那么我们可以在协方差矩阵中减去这些值。 然后我们剩下一个矩阵，仅由潜在公因子的方差和协方差构成。 然后我们可以使用主成分分析方法来分解这些矩阵，并寻找公因子。 这是我们在探索性因子分析中使用的求解过程的本质。 在主成分分析中，我们分解相关矩阵 $\mathbf{R}$（对角线元素都是 1）。 但是对于公因子模型，我们分解对角线元素为 $1 - \theta_{ii}^2$ 的相关矩阵。 实际上，我们通过在模型中减去由于特殊因子引起的变异开始 （回想一下，这些变异可以被解释为测量误差或其他针对于不同考试的变异源，而且和其他因子不相关）， 仅在对角线上保留共同度。 然后我们尝试使用公因子解释剩下的变异。 如果我们知道共同度，那么我们就可以使用与主成分分析相同的方法解决这个问题。 这有时被称为（或简单的被称为公因子模型的主成分方法）。 共同度的估计是这个求解过程中非平凡的部分，有许多不同的方法。

现在让我们假设我们不知道在我们这个解释性示例中由于特殊因子引起的变异的大小 （在后续章节中，我们讨论当我们不知道这些值时该怎么办）。 对于这个考试集合，我们假设每个考试中大约一半的变异都有特殊因子产生， 也就是说，我们开始时对所有 $i$设置 $\theta_{ii}^2 = 0.50$ 然后对这个修改的矩阵进行矩阵分解。 特征值如下所示： $$\begin{array}{ccccc} \lambda_1 = 2.187 & \lambda_2 = 1.022 & \lambda_3 = -0.135 & \lambda_4 = -0.089 & \lambda_5 = 0.015 \end{array}$$

首先值得注意的是，这些特征值和主成分分析的特征值有所不同。 并不是所有的特征值都是正的，并且他们的和也不是 $p$ （分析中变量的数目）。 原因是，通过减去由于特殊因子引起的变异，我们减少了需要由公因子解释的剩余的信息。 这个模型中已经由特殊因子解释的变异是 $0.50 + 0.50 + 0.50 + 0.50 + 0.50 = 2.5$， 即 $2.5/5.0 = 50\%$ 的原始五个考试得分的变异。 对角线元素的和也是 $2.5$，即由公因子解释的方差。

现在仍然存在问题：我们需要多少公因子？ 注意到选择提取的因子数量的标准与主成分分析相比多少有点不同变化。 由于有一些解释了一部分变异的特殊因子，我们的目标是使用公因子解释尽可能多的剩余变异。 因此我们寻找有意义地不同于零地特征值。 在这种情况下，是 2，表示我们提取 $c = 2$个公因子。

双因子解的矩阵（即有原始变量和公因子地相关系数组成地矩阵） 如表所示。 这种因子结构的模式表现出前三个考试（篇章理解、句子完成、单词含义）在第一个公因子上载荷更多（所有相关系数都接近0.8）， 而后两个考试（加法和计数）在第二个公因子上载荷更高（所有相关系数都接近0.6）。 这和第一个因子反映学生的文学天赋、第二个因子指示计量天赋的解释一致。

Factor 1Factor 2$PARA$$0.7722$$-0.2351$$SENT$$0.7838$$-0.1576$$WORD$$0.7562$$-0.2372$$ADD$$0.4293$$0.6017$$DOTS$$0.3476$$0.6506$

使用因子载荷，我们也可以通过这两个公因子计算每项考试解释的变异所占的比例。 这个比例被称为。 例如，对于篇章理解考试（$X_1$），公因子解释了考试中 $(0.77)^2 + (-0.24)^2 = 0.65$即 65% 的变异。 这个共同度值比我们一开始在分析中使用的 $1 - \theta_{11}^2 = 0.50$ 的值略高。 这是因为我们的起点是基于一些先验知识，只是近似的。 对于学生的特定样本，精确值更可能是不同的值。

通过跌多过程来修正我们初始估计值是可行的，最终我们会得到一个一致的结果。 我们用第一次因子分析的结果替代我们处是共同度估计值，并再次进行因子分析。 那么，我们将使用新的值 0.65 代替 $X_1$（篇章理解） 对应的对角线上的元素 0.50， 对于其他变量我们也这么做。 我们可以继续一次迭代、两次迭代这个过程，直到它收敛——也就是说，直到两次迭代之间共同度的变化足够小。 这个迭代过程经常被用于共同度的估计。 这个方法有时被称为。

如果我们没有足够的关于我们数据中测量误差的先验知识（即我们的测量中与潜在因子无关的非系统变异）呢？ 我们使用什么来设置共同度的初始估计值？ 一个被广泛使用的方法是， 即在数据集中一个变量中可被其他所有变量解释的方差的大小。 例如，如果我们想使用多元相关平方系数作为作为 $X_1$ （篇章理解）的初始估值， 我们将 $X_1$与其余的变量 $X_2, X_3, X_4, X_5$ 进行回归，并使用 值。

为什么多元相关平方系数是共同度的良好估值？ 因为共同度是由公因子 $\xi$ 所解释的 $X$中方差的占比。 尽管我们因此喜欢用公因子 $\xi$对 $X$ 进行回归，但也仍然存在公因子不可被观测的问题。 但是我们有其余变量 $X$，每个都反映了潜在变量 $\xi$（尽管并不完美）。 因为测量有误差，他们解释 $X$的能力被减弱了。 因此，多元相关平方系数可以作为共同度的下界。 一般地，测量越可靠（即特殊因子有较小的方差），多元相关平方系数作为共同度的估值越准确。

表展示了考试得分数据使用多元相关平方系数作为共同度估值的因子分析结果。 我们使用一个像上述的迭代过程：用修正的共同度估值代替初始值并继续，直到后续的共同度估计值没有明显改变。

表所示的初始的因子载荷和 表所示的最终结果的差异并不显著。 因子模式指向相同的因子本质的解释。 变异的划分也基本相同：由共同因子解释的变异的大小仍然大约是 66%。 对比两个初始估计值，最后两个考试（加法和计数）相关的共同度比前三个低： 对于 $X_4$和 $X_5$，共同度大约是 0.60，而对于 $X_1$，$X_2$和 $X_3$ 共同度大约是 0.70。 如果我们认为这种差异来自于测量误差，那么我们可能得出后两个考试比前两个考试更不可靠的结论。

关于这种共同度的估计方法，需要注意一点。 如果技术考试被省略，仅保留加法作为学生计量天赋的唯一度量，会怎么样？ 在这些情况下，基于多元相关平方系数计算的假发考试的共同度的估值会非常低 （因为前三个考试没有任何一个反映第二个共同因子）。 因此，我们更可能得出加法是一项非常不可靠的考试，但实际上它是一个重要潜在结构的唯一度量。 正是共同度估值的这个问题，导致有人更喜欢主成分分析法而不是因子分析法。

旋转因子解

在下面第严密推导节中我们会看到，公因子模型实际上拥有无穷多解， 每种解都有平等的能力再现观测到的协方差矩阵。 原因是因子解的方向（即描述坐标系统的基向量的选择）是非常随意的。 这被称为公因子模型的。 在主成分分析中，为了避免不确定性，我们将问题这样定义： 第一主成分是原始数据（经过合理缩放）具有最大方差的线性组合， 第二主成分是拥有次大方差（条件是与第一主成分不相关）的线性组合，等等。 这保证了唯一（尽管有些随意）解。

如果因子解的方向是非常随意的，那么为什么不选择一个可以更好地帮助我们理解并解释数据的解？ 使用因子载荷矩阵尝试提出潜在公因子的一个明确解释往往是比较头疼的。 如果我们可以通过旋转因子解选择一个不同的方向使载荷矩阵得到简化则是非常有利的。 问题就是，如何选择这个方向？ 如何使变化因子载荷矩阵的目标变得可操作，使我们可以找到让我们更接近那个目标的因子解的旋转方式？

寻找这个旋转矩阵 $\mathbf{T}$（我们暂时将讨论限制在正交旋转矩阵范围内，这保留了潜在公因子的独立性）最流行的方法 是基于 Thurstone （1947）描述简单结构原则。 Thurstone 认为大多数内容域可能涉及几个隐藏的（即潜在的或不可观测的）因子。 他同样假设任何一个观测到的变量可能和一个或几个潜在因子相联系，而且任何一个因子可能仅和几个变量相联系。 那么最一般的想法，只要可能，就是找到几个变量簇，每个簇仅明确一个因子。 更一般地，我们想要找到几个因子轴的方向，使得每项考试（或其他变量）尽在几个因子上有相对较高的载荷（正或负）， 而其他因子的载荷趋于零。

如果潜在简单结构的论证有效，那么因子载荷矩阵应该展现出一种特定的模式（Comery，1973）：

1. 大多数特殊因子（列）的载荷应当很小（尽可能接近于零），仅仅一些载荷的绝对值应该很大。
2. 载荷矩阵的某行，包括每个因子的给定变量的载荷，应当在一个或少数因子上表现出非零载荷。
3. 任何一对因子（列）应当展现出不同的载荷模式。否则，这两列所表示的因子无法区分。

一个可以表明简单结构概念的假设例子如表和图所示。 设想一个对消费者对止痛药的看法的研究，其中要求每个受试者根据六个属性评价他（她）的首选止痛药品牌：

1. 没有副作用
2. 能使人保持清醒
3. 适度依赖性[^2]

在表中第一部分所示的因子载荷矩阵是未经旋转的双因子分析的解。 （回想一下，这些未旋转的因子通过使第一个公因子解释最多变异、 第二个公因子在与第一个公因子物馆的条件下尽可能解释更多剩下的变异而定向。） 注意到所有载荷矩阵的 12 个元素都相对较大（绝对值都大于 0.4）。 有这么多重大交叉载荷，获得因子的简单解释就变得比较困难。

未旋转解旋转的解特性Factor 1Factor 2Factor 1Factor 2不反胃$0.579$$-0.452$$0.139$$0.721$没有副作用$0.522$$-0.572$$0.017$$0.774$能止痛$0.645$$0.436$$0.772$$0.097$起效快$0.542$$0.542$$0.764$$-0.051$能使人保持清醒$-0.476$$0.596$$-0.034$$-0.762$适度依赖性$-0.613$$-0.439$$-0.750$$-0.074$解释的方差解释的方差$1.921$$1.562$$1.765$$1.718$

图绘制出因子载荷， 并展示旋转因子空间使特性更接近地位于公因子附近如何成为可能。 想法是选择一个旋转角，使每个特性在公因子上地投影要么很大（即绝对值将近1）要么很小（绝对值接近 0）。 这实际上减小了交叉载荷并在简单结构方向上移动了载荷矩阵。

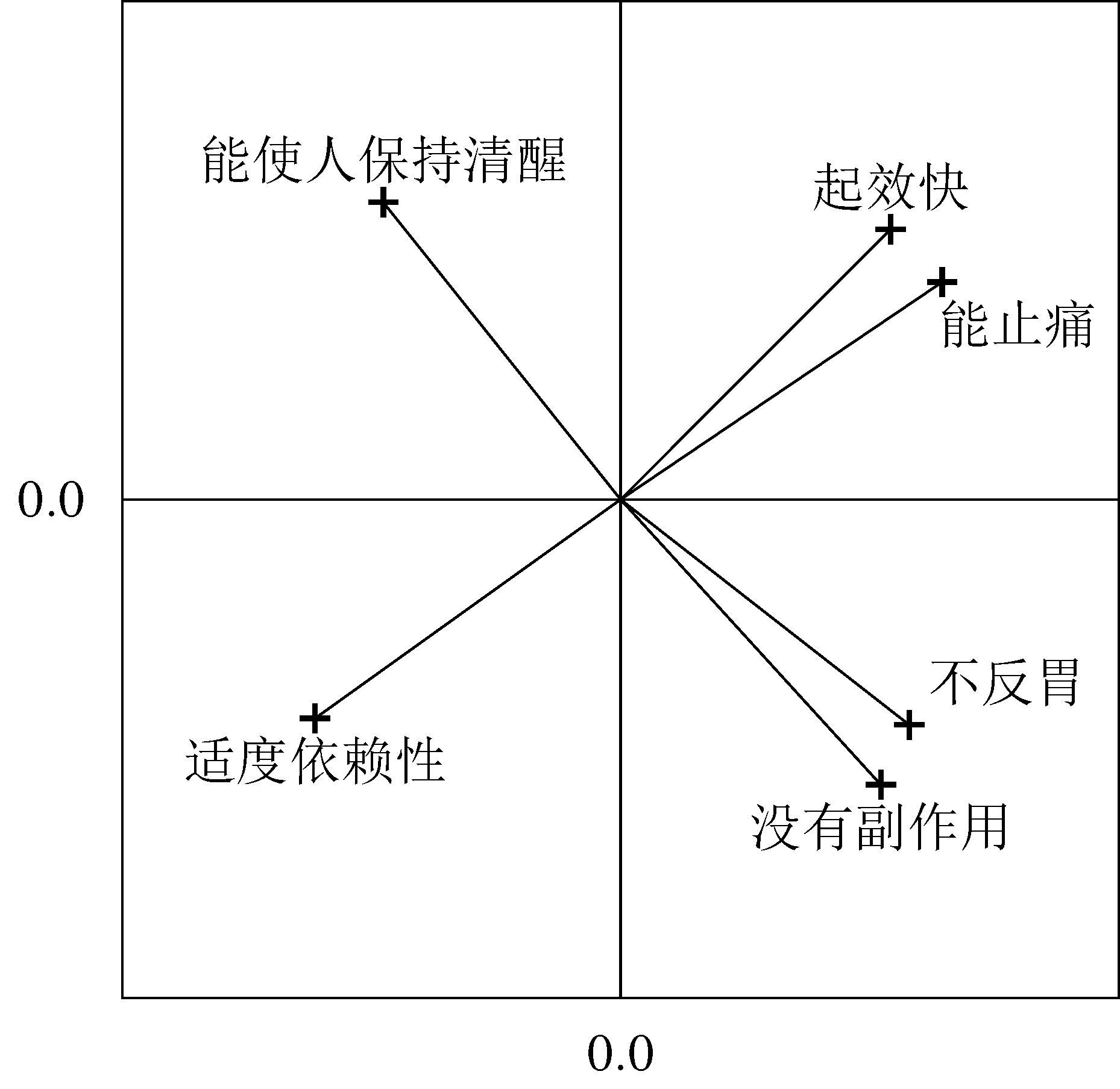
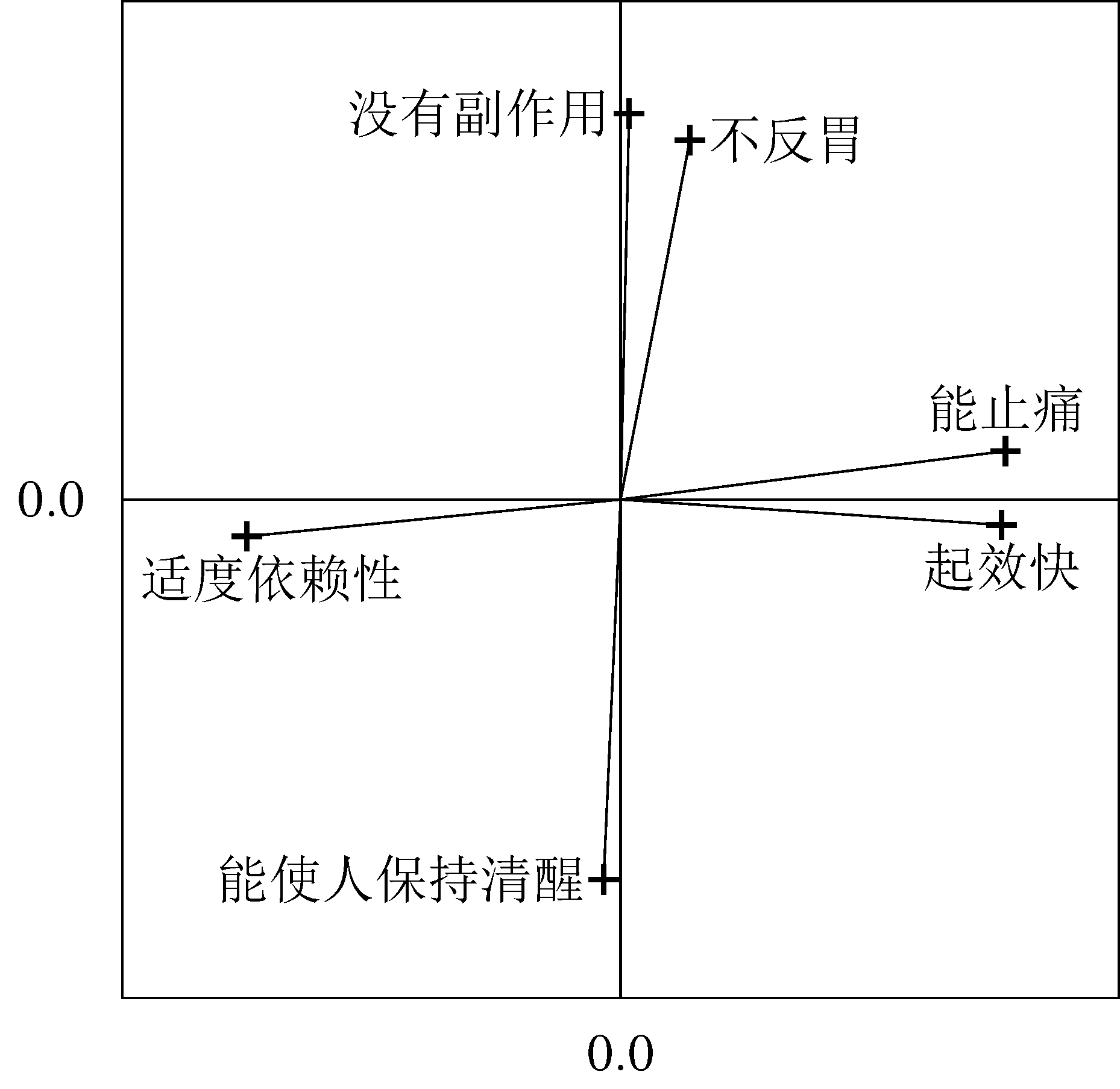
表所示的旋转的因子载荷矩阵展示了接近简单结构的东西。 特性 3 和 4（”能止痛”和”起效快”）在第一个公因子上有正载荷，特性 6（适度依赖性）有负载荷。 特性 1 和 2（”不反胃”和”没有副作用”）在第二个公因子上有正载荷， 特性 5（”能保持清醒”）有负载荷。 所有其他的载荷的绝对值都很小。 给定定义每个因子的属性簇，我们可以标记第一个因子为”有效性”和第二个因子”温和性”。 （负载荷反映负相关。例如，”能保持清醒”的得分越高，”温和性”得分越低。）

需要注意的是，旋转过后，初始因子方向方差最大化的性质就丢失了； 也就是说，虽然总体上保留的因子能够解释与原先的数据集中一样多的变异， 但这种变异现在在旋转配置的新维度上有所不同。 因此，第一个（旋转后的）因子解释最大的变异的情况不存在了。 由于每个因子解释的变异的大小通常并不是关心的主要目标， 如果旋转后的解更容易解释，那么这种取舍通常认为是值得的。

在这个更形式化的因子分析模型的处理中，回到主成分分析模型的建立过程中是非常有用的。 我们已经介绍了，对主成分分析问题的求解等同于对标准化的数据矩阵 $\mathbf{X}$ 进行奇异值分解，如下所示： $$\mathbf{X} = \mathbf{Z}{\mathrm{s}} \mathbf{D}^{\frac{1}{2}}\mathbf{U}^{\mathrm{T}}$$ 其中 $\mathbf{Z}{\mathrm{s}}$是标准化的主成分（全都互不相关）， $\mathbf{D}^{\frac{1}{2}}$是对角线元素全为主成分标准差的对角矩阵， $\mathbf{U}$ 是特征向量矩阵（全都互相正交）。 据此，我们可以将样本相关矩阵 $\mathbf{R}$ 重写为奇异值分解得到的特征值和特征向量的函数。 相关系数矩阵为 $$\mathbf{R} = \frac{1}{n-1} \mathbf{X}^{\mathrm{T}} \mathbf{X}$$ 带入式中的奇异值分解结果到式中并简化可得 $$\begin{aligned} \mathbf{R} & = \frac{1}{n-1}(\mathbf{Z}{\mathrm{s}} \mathbf{D}^{\frac{1}{2}}\mathbf{U}^{\mathrm{T}})^{\mathrm{T}}(\mathbf{Z}{\mathrm{s}} \mathbf{D}^{\frac{1}{2}}\mathbf{U}^{\mathrm{T}}) \ & = \frac{1}{n-1}\mathbf{U}\mathbf{D}^{\frac{1}{2}}(\mathbf{Z}{\mathrm{s}}^{\mathrm{T}}\mathbf{Z}{\mathrm{s}})\mathbf{D}^{\frac{1}{2}}\mathbf{U}^{\mathrm{T}} \ & = (\mathbf{U}\mathbf{D}^{\frac{1}{2}})(\mathbf{U}\mathbf{D}^{\frac{1}{2}})^{\mathrm{T}} \end{aligned}$$ 因为 $\frac{1}{(n-1)}\mathbf{Z}{\mathrm{s}}^{\mathrm{T}}\mathbf{Z}{\mathrm{s}}$正好是一个单位阵。 如果我们继续回忆，矩阵乘积 $\mathbf{U}\mathbf{D}^{\frac{1}{2}}$正好是因子载荷矩阵 $\mathbf{F}$（即原始数据矩阵 $\mathbf{X}$和主成分矩阵 $\mathbf{Z}$的相关系数矩阵）， 我们可以 $\mathbf{R}$的表达式简化为如下形式： $$\mathbf{R} = \mathbf{F}\mathbf{F}^{\mathrm{T}}$$

由于我们使用主成分分析的目标往往是降维，所以我们尝试提取由 $c$ 个成分组成的子集 （其中 $c < p$，$p$是 $\mathbf{X}$中变量的个数）以近似 $\mathbf{R}$。 因此，在主成分中有 $$\mathbf{R} \approx \mathbf{F}_c\mathbf{F}_c^{\mathrm{T}}$$ 其中 $\mathbf{F}_c$仅由因子载荷矩阵 $\mathbf{F}$ 的前几列组成。

在探索性因子分析中，我们同样尝试近似相关矩阵 $\mathbf{R}$，但是使用一个不同的模型。 在式中不是将 $\mathbf{X}$ 的奇异值分解代入，而是使用上述的公因子模型。 有 $c$ 个公因子的一般化模型写作： $$\begin{aligned} X_1 & = \lambda_{11}\xi_{1} + \lambda_{12}\xi_{2} + \cdots + \lambda_{1c}\xi_{c} + \delta_1 \ X_2 & = \lambda_{21}\xi_{1} + \lambda_{22}\xi_{2} + \cdots + \lambda_{2c}\xi_{c} + \delta_2 \ X_3 & = \lambda_{31}\xi_{1} + \lambda_{32}\xi_{2} + \cdots + \lambda_{3c}\xi_{c} + \delta_3 \ & \vdots \ X_p & = \lambda_{p1}\xi_{1} + \lambda_{p2}\xi_{2} + \cdots + \lambda_{pc}\xi_{c} + \delta_p \ \end{aligned}$$ 使用矩阵的形式，公因子模型表示为： $$\begin{aligned} \mathbf{X} = \mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}} + \mathbf{\Delta} \end{aligned}$$ 其中 $\mathbf{\Xi} = [\xi_1, \xi_2, \cdots, \xi_c]$，$\mathbf{\Delta} = [\delta_1, \delta_2, \cdots, \delta_n]$， $\mathbf{\Lambda}_c$是一个 $p \times c$的系数矩阵。 另外，我们使用下面三个关于公因子模型成分的假设

1. 公因子 $\xi$互不相关，且有单位方差 $$\frac{1}{n-1}\mathbf{\Xi}^{\mathrm{T}}\mathbf{\Xi} = \mathbf{I}$$
2. 特殊因子 $\delta$互不相关，且拥有对角化协方差矩阵 $$\mathbf{\Theta} = \frac{1}{n-1}\mathbf{\Delta}^{\mathrm{T}}\mathbf{\Delta} = \mathrm{diag}(\theta_{11}, \theta_{22}, \cdots, \theta_{pp})$$
3. 公因子 $\xi$和特殊因子 $\delta$互不相关 $$\mathbf{\Xi}^{\mathrm{T}}\mathbf{\Delta} = \mathbf{0}$$

现在我们将公式 $$\mathbf{R} = \frac{1}{n-1} \mathbf{X}^{\mathrm{T}} \mathbf{X}$$ 中的 $\mathbf{X}$ 用公式 $$\mathbf{X} = \mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}} + \mathbf{\Delta}$$ 代替， 来对相关系数矩阵 $\mathbf{R}$ 进行近似： $$\begin{aligned} \mathbf{R} & = \frac{1}{n-1}(\mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}} + \mathbf{\Delta})^{\mathrm{T}}(\mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}} + \mathbf{\Delta}) \ & = \frac{1}{n-1}( \mathbf{\Lambda}_c\mathbf{\Xi}^{\mathrm{T}}\mathbf{\Xi}\mathbf{\Lambda}_c + \mathbf{\Delta}^{\mathrm{T}}\mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}} + \mathbf{\Lambda}_c\mathbf{\Xi}^{\mathrm{T}}\mathbf{\Delta} + \mathbf{\Delta}^{\mathrm{T}}\mathbf{\Delta} ) \end{aligned}$$ 基于公因子模型的假设 3，上式圆括号中的第二项和第三项为零。 基于假设 1，第一项中的表达式 $\frac{1}{(n-1)}\mathbf{\Xi}^{\mathrm{T}}\mathbf{\Xi}$可以替换为单位矩阵 $\mathbf{I}$。 基于假设 2，最后一项的表达式变为 $\mathbf{\Theta}$。 通过这些简化，我们可以得到 $$\mathbf{R} = \mathbf{\Lambda}_c\mathbf{\Lambda}_c^{\mathrm{T}} + \mathbf{\Theta}$$ 或者 $$\mathbf{R} - \mathbf{\Theta} = \mathbf{\Lambda}_c\mathbf{\Lambda}_c^{\mathrm{T}}$$

将主成分分析模型的公式 $$\mathbf{R} \approx \mathbf{F}_c\mathbf{F}_c^{\mathrm{T}}$$ 和公因子模型的公式 $$\mathbf{R} - \mathbf{\Theta} = \mathbf{\Lambda}_c\mathbf{\Lambda}_c^{\mathrm{T}}$$ 进行对比，可以发现这两个方法之间的相似性以及本质区别。 两种情况下，我们都是对一个二次对称矩阵进行分解。 矩阵 $\mathbf{\Lambda}_c$ 事实上与矩阵 $\mathbf{F}_c$同构： 是因子载荷矩阵，其元素可被解释为原始变量 $\mathbf{X}$和提取的 $c$个公因子的相关系数。

旋转不确定性

在主成分分析中，我们按顺序方式选择每个成分，以解释原始数据中尽可能大的变异，条件是与所有先前选定的主成分不相关。 这确保了一个唯一解，虽然在选择的方向上有点武断。 但是在公因子模型中，我们没有强加这种约束。 结果是，事实上有无穷多解，他们对矩阵 $\mathbf{R} - \mathbf{\Theta}$ 能够近似的程度是相同的。 我们将这个属性称为公因子模型的。

我们首先通过一个例子来展示这种不确定性。 考虑表所示的考试的分数据的双因子解。 图展示了由该表中因子载荷矩阵所绘制的图表。 我们现在通过将他们顺时针旋转30°来改变因子的方向。 旋转（通过矩阵乘法进行）保留了两个因子的正交性。 由章节，我们知道进行正交旋转（二维）的矩阵具有以下形式： $$\mathbf{T} = \begin{pmatrix} \cos\alpha & -\sin\alpha \ \sin\alpha & \cos\alpha \end{pmatrix}$$ 当旋转角 $\alpha = -30$ 度时，我们得到下列正交旋转矩阵 $\mathbf{T}$ $$\mathbf{T} = \begin{pmatrix} 0.866 & 0.500 \ -0.500 & 0.866 \end{pmatrix}$$

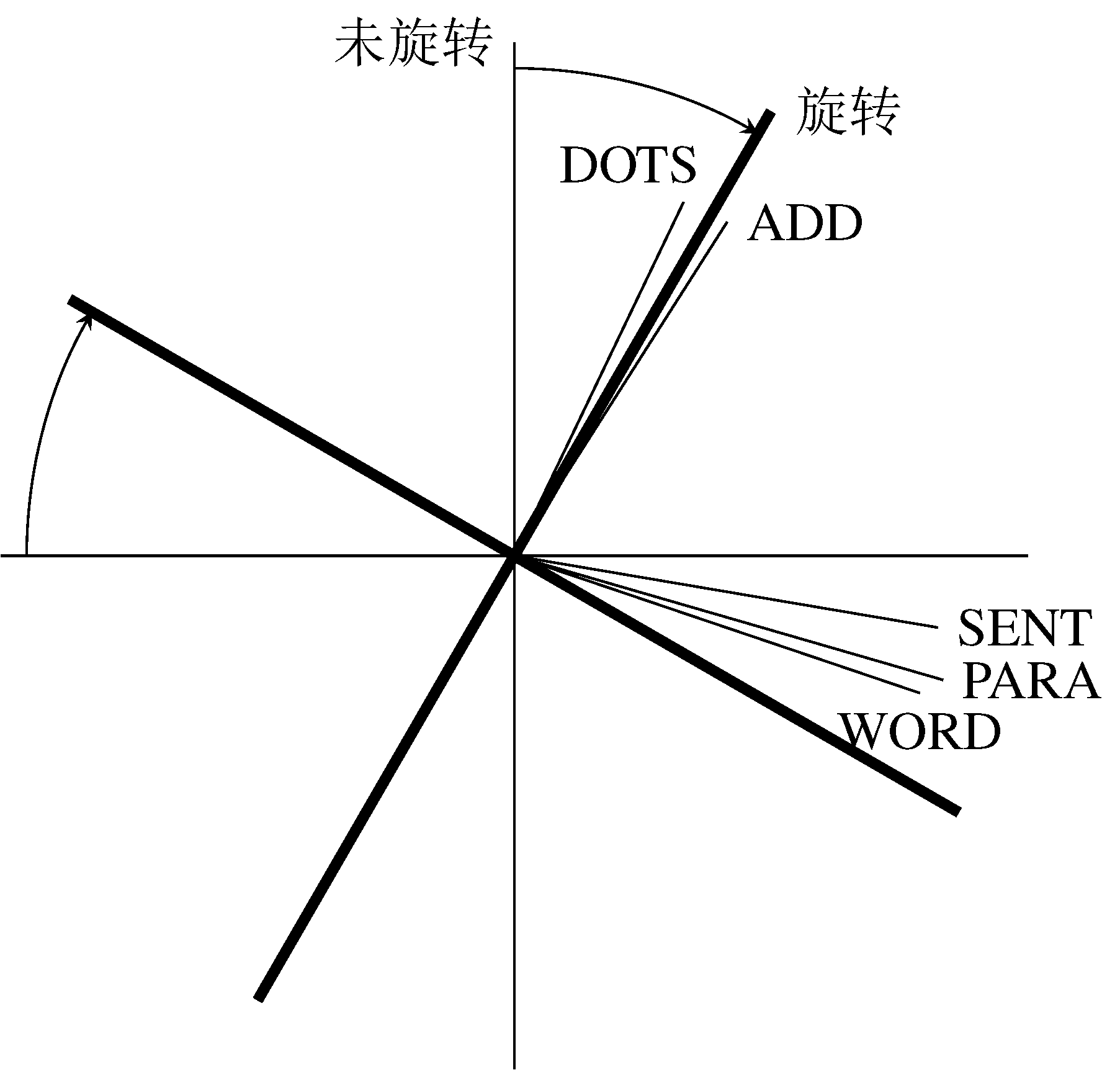
通过改变代表公因子的轴的方向，我们也改变了因子载荷的值。 我们可以计算新的载荷（记为 $\mathbf{\Lambda}_c^$），正好是旋转后的因子 $\mathbf{\Xi}\mathbf{T}$和原始变量 $\mathbf{X}$（由 $\mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}} + \mathbf{\Delta}$ 给出）的相关系数，简化为 $$\mathbf{\Lambda}_c^ = \frac{1}{n-1}(\mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}}+\mathbf{\Delta})^{\mathrm{T}}\mathbf{\Xi}\mathbf{T}$$ 由于 $\frac{1}{(n-1)}\mathbf{\Xi}^{\mathrm{T}}\mathbf{\Xi} = \mathbf{I}$且 $\mathbf{\Delta}^{\mathrm{T}}\mathbf{\Xi} = 0$。 旋转后的因子载荷 $\mathbf{\Lambda}_c^*$ 如表中原始未旋转载荷的旁边所示。 正如之前所说的，矩阵中的主要载荷（即那些拥有高绝对值的载荷）并没有发生显著改变： 前三项考试在第一个因子的载荷和后两个在第二个因子的载荷。 但是注意旋转后的解的交叉载荷改变了。 前三项考试现在在第二个因子上由正载荷（而不是负载荷）， 而后两项考试则几乎完全负载在第二个因子上（而不是在两个因子上都有正载荷）。

关于旋转因子解有两个重要的性质。 第一，尽管每个因子解释的方差发生了变化，两个因子解释的总方差仍然相同。 因为未旋转的解由分解矩阵 $\mathbf{R} - \mathbf{\Theta}$获得， 这个解的方向使第一个因子能够解释最多的变异、第二个因子能够解释剩下的变异。 旋转改变了方向，使得由第一个因子解释的变异变小了。 但是旋转仅改变公因子空间轴的方向，所以并不影响解释的总方差。

第二个旋转解的性质使共同度没有改变。通过从旋转的因子载荷重构矩阵 $\mathbf{R} - \mathbf{\Theta}$可以很容易发现这一性质。 我们有 $$\begin{aligned} \mathbf{R} - \mathbf{\Theta} & = \mathbf{\Lambda}_c^{\mathbf{\Lambda}_c^}^{\mathrm{T}} \ & = \mathbf{\Lambda}_c\mathbf{T}(\mathbf{\Lambda}_c\mathbf{T})^{\mathrm{T}} \ & = \mathbf{\Lambda}_c\mathbf{T}\mathbf{T}^{\mathrm{T}}\mathbf{\Lambda}_c^{\mathrm{T}} \ \end{aligned}$$ 进行矩阵乘法，很容易发现 $\mathbf{T}\mathbf{T}^{\mathrm{T}} = \mathbf{I}$ ： $$\begin{pmatrix} \cos^2\alpha + \sin^2\alpha = 1 & -\cos\alpha\sin\alpha + \sin\alpha\cos\alpha = 0 \ \sin\alpha\cos\alpha - \cos\alpha\sin\alpha = 0 & \cos^2\alpha + \sin^2\alpha = 1 \ \end{pmatrix}$$ 更一般地，任何维度的任何正交旋转矩阵都有 $\mathbf{T}\mathbf{T}^{\mathrm{T}} = \mathbf{I}$。 这是因为矩阵转置实际上将轴按照反方向转了回去，得到了最初的方向。

共同度和被公因子解释的变异以及公因子模型的拟合都不受正交旋转的影响， 这一重要结论在后面我们考虑增强因子解的可解释性时会非常有用。

为了找到最合适的旋转，我们必须找到一种方法以目标函数的形式定量化表达通过简化结构我们想要什么。 然后我们搜索所有可能的旋转角度，然后选择矩阵 $\mathbf{T}$ 使满足旋转后的因子载荷矩阵 $\mathbf{A} = \mathbf{\Lambda}_c\mathbf{T}$ 对于简化的结构展现出高的目标函数的值。 有许多不同的方法来量化最简结构，我们只讨论两个： Kaiser 的最大方差正交旋转法和四次方最大旋转法。

Kaiser 的最大方差正交旋转法

回忆旋转后的载荷矩阵每个元素 $a_{ik}$可以被解释为变量 $i$和公因子 $k$ 间的相关系数。 载荷的平方 $a_{ik}^2$是变量 $i$中由公因子 $k$ 引起的变异的比例。 由于我们所选择的公因子互不相关，所有公因子所能解释的变异大小之和——即所谓的共同度——可以由载荷平方和给出， 也就是 $h_i^2 = \sum_k a_{ik}^2$。 为了实现最简结构，我们想要找到一个旋转使得平方载荷 $a_{ik}^2$要么接近 1，要么接近 0。

最大方差过程通过关注 $\mathbf{A}$的列来尝试实现这一目的：它选择旋转矩阵 $\mathbf{T}$ 来最大化 $a_{ik}^2$的列方差之和。 第 $k$个列方差由下式给出 $$V_k = \frac{1}{p} \sum_{i=1}^{p}\left(a_{ik}^2\right)^2 - \frac{1}{p^2}\left(\sum_{i=1}^{p}a_{ik}^2\right)^2$$ 对所有因子 $k$最大化列方差 $V_k$之和等同于最大化下式 $$V = \sum_{k=1}^{c}\sum_{i=1}^{p}a_{ik}^4 - \frac{1}{p}\sum_{k=1}^{c}\left(\sum_{i=1}^{p}a_{ik}^2\right)^2$$ 注意到当 $a_{ik}^2$的值趋向于 0 或 1 时可以得到最大方差； 根据定义，对于某些因子 $k$，当 $a_{ik}^2$的值趋向于 1，所有其他在矩阵中同一行上的项都趋于 0。

对于最大方差正交旋转法使用归一化平方载荷（$\frac{a_{ik}^2}{h_i^2}$）建立目标函数也是可能的。 如果使用这种方式归一化载荷，$\frac{a_{ik}^2}{h_i^2}$可以被解释为 变量 $i$由于公因子 $k$引起变异大小的比例。 使用这种归一化确保在选择旋转时所有矩阵由相同的权重 （当一些变量有较低共同度时对于没有归一化的平方载荷则不是这种情况）。

四次方最大旋转法

与最大方差正交旋转法关注旋转的因子载荷矩阵 $\mathbf{A}$ 的列不同，四次方最大旋转法关注行。 四次方最大旋转法的目标函数依赖于正交旋转前后变量的共同度不变这一事实； 因此，表达式 $\sum_k a_{ik}^2$是常数，与旋转矩阵 $\mathbf{T}$无关。 对于所有变量，共同度的平方和 $\sum_i(\sum_k a_{ik}^2)^2$也是一个常数。 扩展这个表达式得到 $$\sum_{i=1}^{p}\sum_{k=1}^{c} a_{ik}^4 + \sum_{i=1}^{p}\left(\sum_{k=1}^{c}\sum_{j\neq k}a_{ik}^2a_{ij}^2\right)$$

上式的第二项是平方载荷的交叉积。当矩阵具有简单结构时，该积应当尽可能小 （即当一个变量在因子 $k$上有高载荷，对其他所有因子 $j$载荷应当接近 0）。 因为上式对于所有旋转矩阵 $\mathbf{T}$ 是常数，一种保证交叉积项最小的方法是最大化表达式的第一项。 因此，四次方最大旋转法选择一个正交旋转矩阵 $\mathbf{T}$使 $$Q = \sum_{i=1}^{p}\sum_{k=1}^{c} a_{ik}^4$$ 最大。与最大方差正交旋转法相同，在进行旋转之前，可以对平方载荷通过除以变量的共同度进行归一化。

我们在下面的章节中讨论倾斜旋转（旋转不能保持因子的相互正交性）的问题。

通常，因子分析本身并不是目的，而是进一步分析数据的中间步骤。 对于后续分析，我们需要获得在缩减的因子空间中每个原始观测的位置。 这个值被称为。

从公因子模型中得到因子得分并不像从主成分分析中得到成分得分一样容易。 回想一下，主成分得分是原始变量的线性组合，可以使用来自相关矩阵的特征向量的系数直接计算。 在公因子分析中，由于特定因素引入的不确定性，得分无法准确计算。 换句话说，在公因子模型中我们不能将 $\xi$在不知道 $\delta$的情况下写成 $X$的函数。

因此，有必要估计我们将在计算因子得分时使用的因子得分系数。 我们用下述线性表达式近似 $\mathbf{\Xi}$ $$\mathbf{\Xi} = \mathbf{X}_s\mathbf{B}$$ 其中 $\mathbf{B}$时因子得分系数矩阵。由于 $\mathbf{\Xi}$ 的值不能直接被观测到，我们不能使用最小二乘回归计算 $\mathbf{B}$。 但是，如果我们对上式两边同时乘以 $\frac{1}{(n-1)}\mathbf{X}_s^{\mathrm{T}}$我们可以得到 $$\frac{1}{n-1}\mathbf{X}_s^{\mathrm{T}}\mathbf{\Xi} = \frac{1}{n-1}\mathbf{X}_s^{\mathrm{T}}\mathbf{X}_s\mathbf{B}$$ 或 $$\mathbf{\Lambda}_c = \mathbf{R}\mathbf{B}$$

在保证等式不变的情况下，我们将两边同时乘以 $\mathbf{R}^{-1}$，对于因子得分系数有 $$\mathbf{B} = \mathbf{R}^{-1}\mathbf{\Lambda}_c$$ 将这个式子中的 $\mathbf{B}$ 代入式中得到用于估计因子得分的下式 $$\mathbf{\Xi} = \mathbf{X}_s \mathbf{R}^{-1} \mathbf{\Lambda}_c$$

注意到由于载荷矩阵 $\mathbf{\Lambda}_c$ 满足旋转不确定性，式得到的因子得分 并不唯一，并且具有相同的旋转不确定性。但是乘积 $\hat{\mathbf{X}}_c = \mathbf{\Xi}\mathbf{\Lambda}_c^{\mathrm{T}}$是不变的， 其中 $\hat{\mathbf{X}}_c$由 $c$ 个潜在因子拟合的 $\mathbf{X}$的一部分。

[^1]: 译者注：原文中没有明确表示”不同”的 $i$和 $j$，但此处确实应不相同。 若相同，则 $\mathrm{corr}(\delta_i,\delta_j) = 1$ 而不是 $0$。

[^2]: 原文：Provides limited relief.