一元函数自动求解器 – 牛顿法的实现

在阅读本文之前，请先看一道题：求解x，使得 e−x−x=0e−x−x=0

如果你能用纸笔解出这道题的话，请务必留言告知我方法，谢谢。

如果你不能用纸笔解出这道题的话，那么我们可以完全借助代码来对其进行求解。

以下就是我写的求解器，它几乎能够对所有的一元函数进行自动求解。

你可以在输入框内尝试任意一元函数，按Enter键或点击求解按钮进行求解。如有bug请留言，谢谢。

它的原理有一点复杂，下面将会一一讲到。

牛顿法是求解的核心方法，它的维基百科的定义为：

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数fxx的泰勒级数的前面几项来寻找方程fxx=0的根。

简言之，牛顿法就是对x进行迭代，直至x收敛于某个很小的范围。

其迭代的公式为：

xn+1=xn–f(xn)f′(xn)xn+1=xn–f(xn)f′(xn)

其中f′(xn)f′(xn)为f(xn)f(xn)的导函数。

要理解牛顿法，你就要了解泰勒展开。牛顿法其实是利用了一阶的泰勒展开：

f(x)=f(x0)+(x−x0)⋅f′(x0)f(x)=f(x0)+(x−x0)⋅f′(x0)

对上述方程 f(x)=0f(x)=0 进行求解，得到：

x=x0–f(x0)f′(x0)x=x0–f(x0)f′(x0)

这就是牛顿迭代公式的逼近原理。

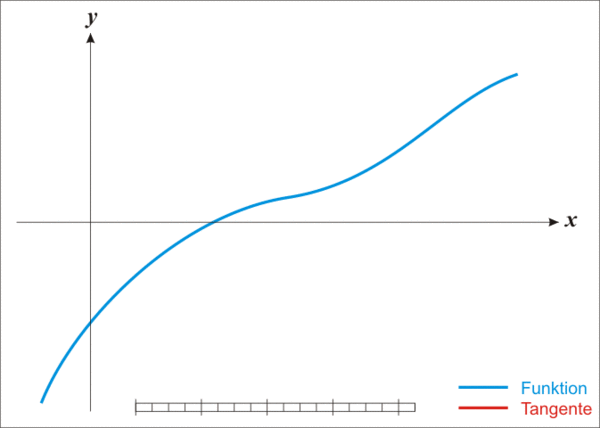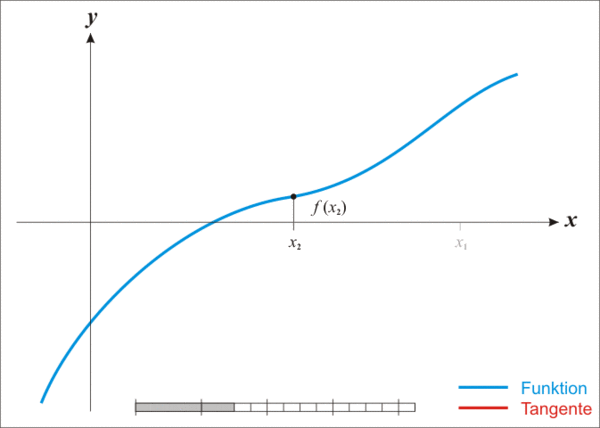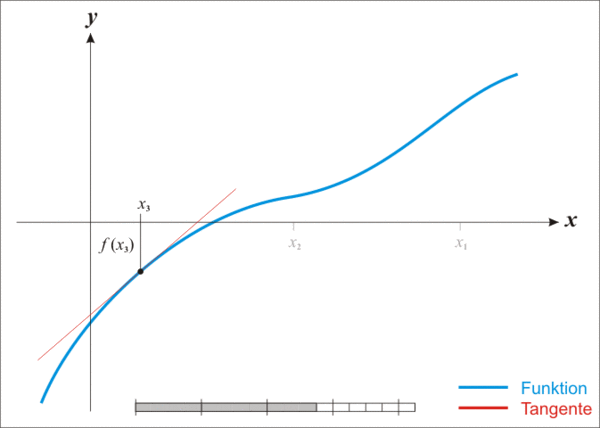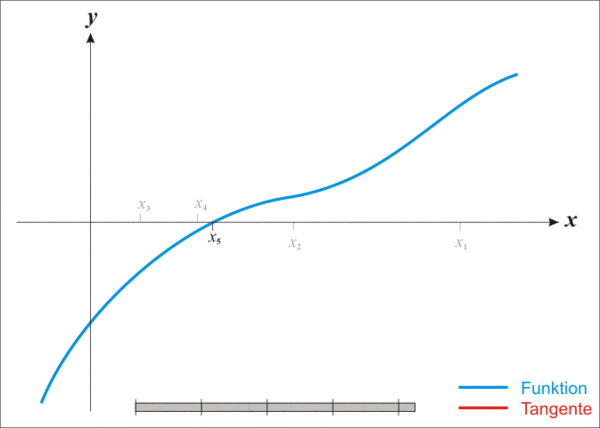
你可以通过这幅图直观的看到x逼近的过程：

所以，对于任意的一元函数，我们都可以尝试用牛顿法来求得其近似解，一个简单伪代码如下：

声明 x0, x1, i

//当误差小于10^-9时，或者迭代步数超过10^5时，迭代结束

while (Math.abs(x0 - x1) > 10E-9) {

//进行迭代

x0 = x1

x1 = x0 - (f(x0) / f'(x0))

//若步数过长，终止迭代

if( i < 10E5) {

break

以下，我们将根据牛顿法，来构建自动求解器。

构建求解器

在构建求解器时，有几个关键问题需要解决：解析输入的表达式，表达函数，求导函数方程，对函数进行代入求值。

其中，最优先的一个问题是：我们怎么储存（表达）函数?

《SICP》的第一章提到了一种表示法：二分表达树。

以下是表达式((5 + z) / -8) * (4 ^ 2)的二分表达树的图例：

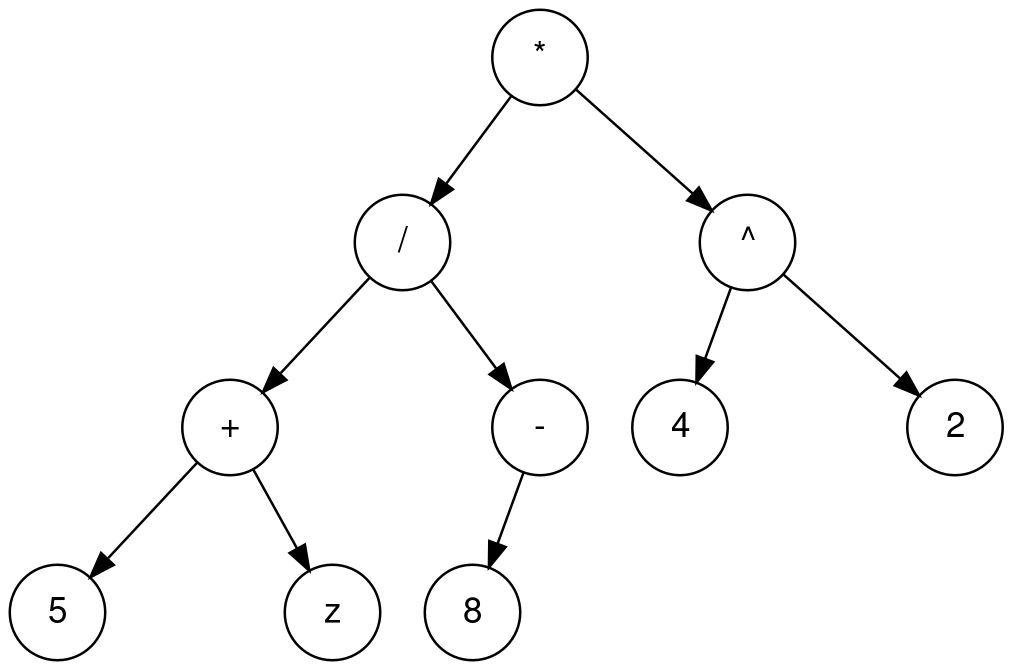
为什么选择这种表达方式呢？

主要是因为它是树形结构，方便递归处理节点，而我们之后求导函数其实就是用的递归思路，包括代入求值也是递归的思路。

预处理表达式

首先，我们需要预处理输入的表达式字符串。因为在数学中有一些简略或者多余的写法需要在此规范化。

5x表示5*x，通常都省略了乘号
.5+x表示0.5+x，省略了小数点前的0
-x中的-其意思是取负操作，是一个单目运算符。为了不与减法冲突，我们也需要将其预处理为(0-x)
+5-x的加号完全没有意义，我们需要将其省去

比如，输入串 .5e^-x-2x，经过预处理后将变成 0.5e^(0-x)-2x。

自然的输入串经过预处理后，就应该是一个中缀的表达式字符串，这是人类能够自然理解的表达式形式。

但是为了将表达式储存成二叉表达树，我们还需要将中缀表达式转换成后缀表达式。

由迪杰斯特拉提出的调度场算法可以解决这个问题。

调度场算法

调度场算法基本和我们在栈递归汉诺塔文中提到的利用栈来计算表达式的方法类似。

它用队列表达输出的后缀表达式，利用了栈来储存操作符和函数。

其详细算法过程为（摘录自维基百科）:

当还有记号可以读取时：
- 读取一个记号。
- 如果这个记号表示一个数字，那么将其添加到输出队列中。
- 如果这个记号表示一个函数，那么将其压入栈当中。
- 如果这个记号表示一个函数参数的分隔符（例如，一个半角逗号 , ）：
  - 从栈当中不断地弹出操作符并且放入输出队列中去，直到栈顶部的元素为一个左括号为止。如果一直没有遇到左括号，那么要么是分隔符放错了位置，要么是括号不匹配。
- 如果这个记号表示一个操作符，记做o1，那么：
  - 只要存在另一个记为o2的操作符位于栈的顶端，并且
    - 如果o1是左结合性的并且它的运算符优先级要小于或者等于o2的优先级，或者
    - 如果o1是右结合性的并且它的运算符优先级比o2的要低，那么
    - 将o2从栈的顶端弹出并且放入输出队列中循环直至以上条件不满足为止循环直至以上条件不满足为止；
  - 然后，将o1压入栈的顶端。
如果这个记号是一个左括号，那么就将其压入栈当中。
如果这个记号是一个右括号，那么：
- 从栈当中不断地弹出操作符并且放入输出队列中，直到栈顶部的元素为左括号为止。
- 将左括号从栈的顶端弹出，但并不放入输出队列中去。
- 如果此时位于栈顶端的记号表示一个函数，那么将其弹出并放入输出队列中去。
- 如果在找到一个左括号之前栈就已经弹出了所有元素，那么就表示在表达式中存在不匹配的括号。
当再没有记号可以读取时：
- 如果此时在栈当中还有操作符：
- 如果此时位于栈顶端的操作符是一个括号，那么就表示在表达式中存在不匹配的括号。将操作符逐个弹出并放入输出队列中。
退出算法。

其分支逻辑比较繁琐，需要细细阅读和小心实践。

构建二叉表达式树

假设输入表达式为：(a+b) * (c * (d+e))，经过调度场算法，我们得到a b + c d e + * *的后缀表达式。

此时我们便可以利用后缀表达式的特点，快速的构建出一颗二叉表达树来。

构建的算法很简单：

新建一个栈
从头到尾遍历后缀表达式，
- 当发现操作数时，我们将其存为操作数节点，入栈；
- 当发现操作符时，我们将其存为操作符节点，
  - 若是二元操作符，我们将栈顶的两个节点弹出，作为该操作符的节点左右节点，然后将该节点入栈
  - 若是一元操作符，我们将栈顶节点弹出，作为该操作符的右节点，然后将该节点入栈

整个过程如果用图来说明，会十分容易理解。

首先我们遍历到a，它是操作数，入栈，b也是操作数，也入栈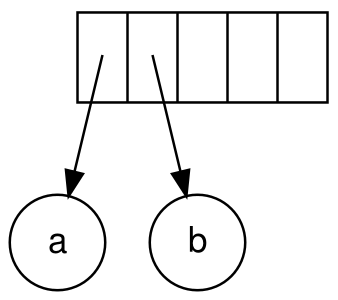
遍历到+，它是二元操作符，弹出两个节点，然后添加至左右节点，入栈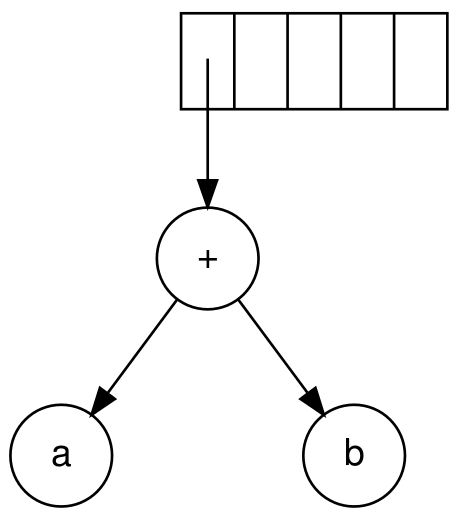
接下来三个都是操作数，将它们都入栈
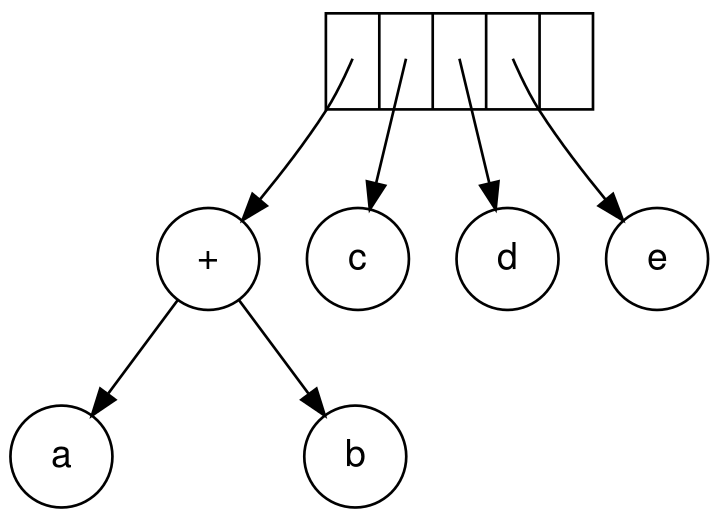
然后遍历到+，同2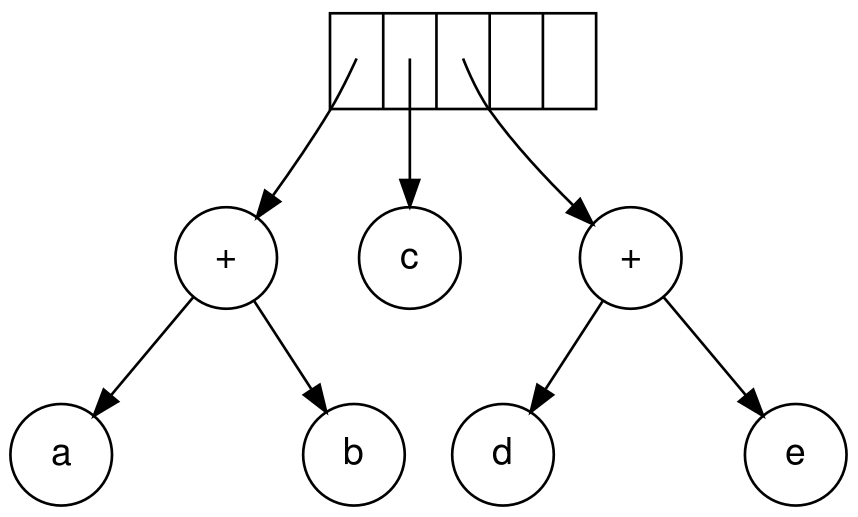
接下来是*，同2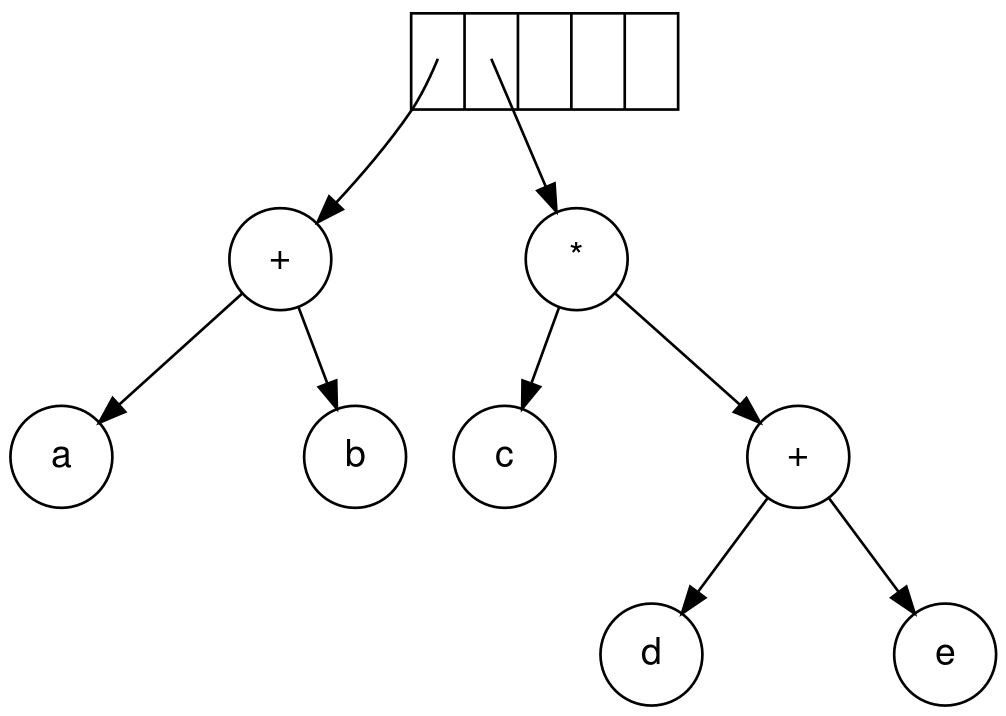
仍然是*，同2；遍历完毕，我们得到如下的二叉表达树：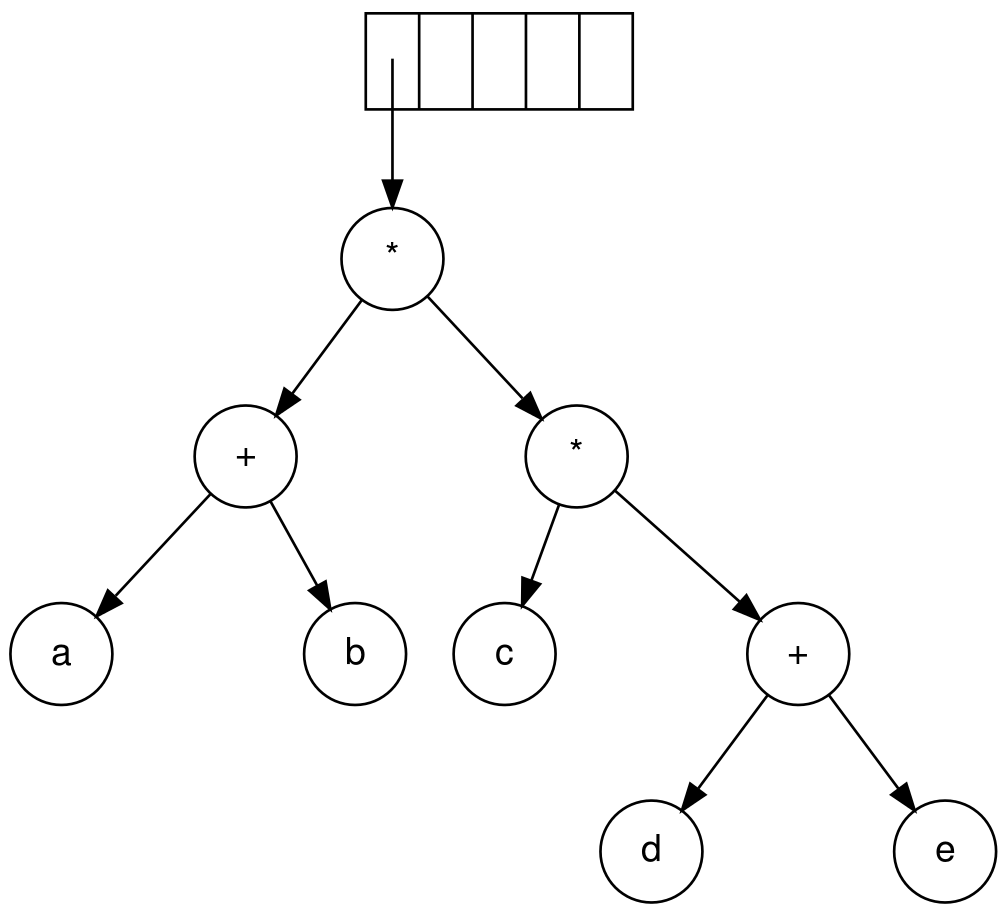

我们定义二叉表达树为如下：

/**二叉表达树*/

function ExpTree(key) {

//根节点

this.root = null;

//未知量的表达形式，默认为x

this.key = key || 'x';

//中序遍历的字符串

this.infix = '';

//后续遍历的字符串

this.postfix = '';

定义树的节点如下：

/**二叉表达树节点*/

function ExpTreeNode(key, left, right) {

//节点值

this.key = key;

//左子树，默认为空

this.left = left || null;

//右子树，默认为空

this.right = right || null;

对二叉表达树进行代入求值的算法应该很容易就能想到。

利用二叉树的递归特性，根为操作符或函数，左子树右子树是递归定义。我们只需要将左右子树的值递归求出，然后在进行操作符运算即可。

代码如下：

/**递归计算表达式的值*/

ExpTree.prototype.cal = function(node, x) {

if(!node) {

return;

//有子树，进行递归运算

if(node.left || node.right) {

//进行操作符运算

return this.op( node.key, this.cal(node.left, x), this.cal(node.right, x) );

//否则，直接返回节点值

switch(node.key) {

case 'x':

return x;

case 'e':

return Math.E;

case 'pi':

return Math.PI;

default:

return node.key;

/**执行原子计算*/

ExpTree.prototype.op = function(opr, left, right) {

switch(opr) {

case '+':

return left + right;

case '-':

return left - right;

case '*':

if(left == 0 || right == 0) {

return 0;

return left * right;

case '/':

return left / right;

case '^':

return Math.pow(left, right);

case 'sin':

return Math.sin(right);

case 'cos':

return Math.cos(right);

case 'tan':

return Math.tan(right);

case 'cot':

return 1 / Math.tan(right);

case 'arcsin':

return Math.asin(right);

case 'arccos':

return Math.acos(right);

case 'arctan':

return Math.atan(right);

case 'ln':

return Math.log(right);

case 'log':

return Math.log(right) / Math.log(left);

default:

//error!

console.log(opr, 'error!');

return 0;

构建导函数树

至此，我们只剩下了求解导函数的步骤。这一步也是比较复杂的操作，因为导函数的规则实在是很多。

请参见导函数的维基百科的定义。

但是重点是，我们用什么方法来求解导函数，又该如何表达导函数呢？

首先，表达导函数应该用二叉表达树来进行表示，因为可以直接对其进行代入求值，而且二叉表达树具有递归的特性；

其次，由于二叉表达树的根节点总是操作符或函数的特性，左右子树也是表达式，我们可以用递归的思路来求解导函数。

主要思路为：对于一个二叉表达树，根节点为操作符或函数，左右子树则为操作符或函数的运算的参数。

比如根节点为+操作，左右子树为a,b：

具体的表达式则为 a+ba+b，我们对加法求导法则是(a+b)′=a′+b′(a+b)′=a′+b′。我们可以发现求导也可以递归表达。即上面那颗二叉树的导函数为根为+，左子树为a的导函数的树，右子树为b的导函数的树。

所以我们可以用递归来表示求导的过程，下面是完全规则的求导代码：

ExpTree.prototype.dao = function(node) {

if(!node) {

return;

var t;

switch(node.key) {

case '+':

case '-':

//l+rl+r' = l' + r'

//l−rl−r' = l' - r'

t = new ExpTreeNode(node.key, this.dao(node.left), this.dao(node.right));

break;

case '*':

//l∗rl∗r' = l'*r + l*r'

t = new ExpTreeNode('+');

t.left = new ExpTreeNode('*', this.dao(node.left), node.right);

t.right = new ExpTreeNode('*', node.left, this.dao(node.right));

break;

case '/':

//l/rl/r' = l′∗r−l∗r′l′∗r−l∗r′ / r∗rr∗r

t = new ExpTreeNode('/');

t.left = new ExpTreeNode('-');

t.left.left = new ExpTreeNode('*', this.dao(node.left), node.right);

t.left.right = new ExpTreeNode('*', node.left, this.dao(node.right));

t.right = new ExpTreeNode('*', node.right, node.right);

break;

case '^':

t = new ExpTreeNode('*');

if(node.right._containParam(node.right)) {

//lrlr' = lrlr * ln(lln(l*r)'

t.left = node;

t.right = this.dao(new ExpTreeNode('*', new ExpTreeNode('ln', null, node.left), node.right));

else {

//lclc' = l′∗cl′∗c * l^c−1c−1

t.left = new ExpTreeNode('*', this.dao(node.left), node.right);

t.right = new ExpTreeNode('^', node.left, new ExpTreeNode('-', node.right, new ExpTreeNode(1)));

break;

case 'sin':

//sinrr' = cosrr*r'

t = new ExpTreeNode('*');

t.left = new ExpTreeNode('cos', null, node.right);

t.right = this.dao(node.right);

break;

case 'cos':

//cosrr' = 0-sinrr*r'

t = new ExpTreeNode('-', new ExpTreeNode(0));

t.right = new ExpTreeNode('*', new ExpTreeNode('sin', null, node.right), this.dao(node.right));

break;

case 'tan':

//tanrr' = r' / cos(rcos(r * cosrr)

t = new ExpTreeNode('/', this.dao(node.right));

t.right = new ExpTreeNode('*', new ExpTreeNode('cos', null, node.right), new ExpTreeNode('cos', null, node.right));

break;

case 'cot':

//cotrr' = 0-r'/sin(rsin(r*sinrr)

t = new ExpTreeNode('-', new ExpTreeNode(0));

t.right = new ExpTreeNode('/', this.dao(node.right));

t.right.right = new ExpTreeNode('*', new ExpTreeNode('sin', null, node.right), new ExpTreeNode('sin', null, node.right));

break;

case 'arcsin':

//arcsinrr' = r' / 1−r∗r1−r∗r^0.5

t = new ExpTreeNode('/', this.dao(node.right))

t.right = new ExpTreeNode('^', null, new ExpTreeNode(0.5));

t.right.left = new ExpTreeNode('-', new ExpTreeNode(1), new ExpTreeNode('*', node.right, node.right));

break;

case 'arccos':

t = new ExpTreeNode('/', this.dao(node.right))

t.right = new ExpTreeNode('^', null, new ExpTreeNode(0.5));

t.right.left = new ExpTreeNode('-', new ExpTreeNode(1), new ExpTreeNode('*', node.right, node.right));

t = new ExpTreeNode('-', new ExpTreeNode(0), t);

//arccosrr' = 0 - r′/(1−r∗rr′/(1−r∗r^0.5)

break;

case 'arctan':

t = new ExpTreeNode('/', this.dao(node.right))

t.right = new ExpTreeNode('+', new ExpTreeNode(1), new ExpTreeNode('*', node.right, node.right));

//arcsinrr' = r' / 1+r∗r1+r∗r

break;

case 'ln':

//lnrr' = r'/r

t = new ExpTreeNode('/', this.dao(node.right), node.right);

break;

case 'log':

//logl,rl,r = r'/r∗ln(lr∗ln(l)

t = new ExpTreeNode('/', this.dao(node.right));

t.right = new ExpTreeNode('*', node.right, new ExpTreeNode('ln', null, node.left));

break;

case 'x':

//x' = 1

t = new ExpTreeNode(1);

break;

default:

//常量的导数为0

t = new ExpTreeNode(0);

break;

return t;

我们把导函数表达成了二叉表达树的形式，至此，我们已经把所有问题全部解决。

求解表达式解的过程将十分清晰：

将输入的表达式构建成表达式树t，同时构建其导函数的表达式树dt
利用牛顿法，进行迭代求解

开放源码

源码地址为：https://github.com/iWoz/DSinJS/blob/master/ExpressionTree/ExpTree.js。

源码集成在JavaScript的算法与数据结构系列中，托管于GitHub:

Demo托管于JsFiddle。

欢迎讨论！

Posted in Alogrithm, DataStructure, DS_in_JS, JavaScript Tagged JavaScript, 数据结构, 求解器, 牛顿法, 算法, 表达树, 递归

关注微信公众号：timind

8 responses

krator

2014/04/25 02:19

有点意思，如果有求解析解的就霸气了。
求微分的英文单词是derivation

回复
- Tim
  
  2014/04/25 10:06
  
  开个玩笑，如果我能求解析解，我将会获得图灵奖或菲尔兹奖。
  
  举个栗子，一元高阶方程至今没有解析解的解法。
  
  你看文章很仔细，估计你也有强迫症。。但是我人比较懒，所以就写成了dao
  
  BTW，微分的英文是Differential，导数的英文是derivative。这两者是不同的概念。
  
  回复
尚吾网

2014/04/25 10:11

坚持更新博客就像坚持写日记一样，不仅是习惯，也是耐力，表示支持

回复
我是来围观的

2014/05/06 13:48

猩猩，赞一个！怎么开始研究数值计算了- –

回复
在线工具

2015/10/22 12:58

很赞，我收录到工具里面来了。
最后附有贵博客地址：http://www.atool.org/function_solver.php

回复
fl

2018/01/16 10:18

你好，2个bug

1. x=0
说是格式不对

2. x^x+1x+1=0
这个解不了

回复
fll

2018/06/20 09:42

最好增加一个功能：求解范围的指定，例如仅求解a,ba,b开区间内的解。
当然不指定求解区间的功能还是保留下来。

回复