完美迷宫生成算法

Perfect maze

Perfect maze又称standard maze，指没有回路，没有不可达区域的迷宫。用图论的语言来说，就是可以用spanning tree表示的迷宫，保证迷宫中任意两个格子间都有唯一的路径。本文旨在探讨如何随机生成棋盘状perfect maze。迷宫格子的邻居的定义采用von Neumann neighborhood，即水平竖直方向相邻的四个格子。

变形Kruskal算法

说得通俗点，就是“随机拆墙”。

一开始假设所有墙都在。如果当前不满足“任意两个格子间都有唯一路径”，那么就随机选择一堵墙，要求墙两端的格子不连通，即它们对应的两个顶点不在一个connected component里。

把这堵墙拆掉，即在后墙两端的格子对应的顶点间建立一条边，此时connected component数就减少一了。不断地找墙、拆墙，最后就能形成一个看上去挺随机的迷宫。

W = 所有墙
T = {}
number_of_components = N*N
while number_of_components > 1
  (u, v) = W.pop
  if component(u) != component(v)
    T << (u, v)
    merge component(u) and component(v)

最后T集合就是spanning tree中的边，即所需拆除的墙。

考虑转化为图论模型后我们需要的操作，只有两个，即：

判断两个元素是否在一个集合中(两个顶点是否在同一个connected component里)，
合并两个集合(合并两个connected component)。

对于这个问图，有经典的disjoin-set forest算法可以在近似线性的时间复杂度里解决这个问题。

Aldous-Broder算法

很简单，随机选择一个格子作为起点，每次随机选择一个邻居格子走过去，如果目标格子不与当前格子连通则打通它们之间的墙。

Haskell实现

以下代码改编自某个Haskell的recursive backtracking算法：

import Control.Applicative

import Control.Monad

import Control.Monad.Cont

import Control.Monad.ST

import Data.Array

import Data.Array.ST

import Data.STRef

import System.Random

import Debug.Trace

data Maze = Maze { rightWalls, belowWalls :: Array (Int, Int) Bool }

rand :: Random a => (a, a) -> STRef s StdGen -> ST s a

rand range g = do

(a, g') <- liftM (randomR range) $ readSTRef g

a <$ writeSTRef g g'

maze :: Int -> Int -> StdGen -> ST s Maze

maze w h gen = do

let mk = newArray ((0,0), (w-1,h-1)) :: Bool -> ST s (STArray s (Int, Int) Bool)

visited <- mk False

right <- mk True

bottom <- mk True

gen <- newSTRef gen

walk 1 (x,y) = return ()

walk c u@(x,y) = do

writeArray visited u True

let ns = [(x-1,y) | x > 0] ++ [(x+1,y) | x+1 < w] ++ [(x,y-1) | y > 0] ++ [(x,y+1) | y+1 < h] :: [(Int,Int)]

i <- rand (0, length ns - 1) gen

let v@(x', y') = ns !! i

wall = if x == x' then bottom else right

g = (min x x', min y y')

hasWall <- readArray wall g

seen <- readArray visited v

if seen

walk c v

writeArray wall g False >> walk (c-1) v

(,) <$> rand (0, w-1) gen <*> rand (0, h-1) gen >>= walk (w*h)

Maze <$> freeze right <*> freeze bottom

maze :: Int -> Int -> StdGen -> ST s Maze

maze w h gen = do

let mk = newArray ((0,0), (w-1,h-1)) :: Bool -> ST s (STArray s (Int, Int) Bool)

visited <- mk False

right <- mk True

bottom <- mk True

gen <- newSTRef gen

walk 1 gen (x,y) = return ()

walk c gen u@(x,y) = do

writeArray visited u True

let ns = [(x-1,y) | x > 0] ++ [(x+1,y) | x+1 < w] ++ [(x,y-1) | y > 0] ++ [(x,y+1) | y+1 < h] :: [(Int,Int)]

i <- rand (0, length ns - 1) gen

let v@(x', y') = ns !! i

wall = if x == x' then bottom else right

g = (min x x', min y y')

hasWall <- readArray wall g

seen <- readArray visited v

if seen

walk c gen v

writeArray wall g False >> walk (c-1) gen v

(,) <$> rand (0, w-1) gen <*> rand (0, h-1) gen >>= walk (w*h) gen

Maze <$> freeze right <*> freeze bottom

printMaze :: Maze -> IO ()

printMaze (Maze right bottom) = do

putStrLn $ concat (replicate (maxX + 1) "._") ++ "."

forM_ [0..maxY] $ \y -> do

putStr "|"

forM_ [0..maxX] $ \x -> do

putStr $ if bottom ! (x, y) then "_" else " "

putStr $ if right ! (x, y) then "|" else "."

putChar '\n'

where

(maxX, maxY) = snd $ bounds right

main = getStdGen >>= stToIO . maze 12 13 >>= printMaze

该算法的优点是能等概率地生成每一棵spanning tree。

Recursive backtracking算法

上述随机拆墙使用到的Kruskal算法是求minimum spanning tree问题最广为人知的两个算法之一，另一个就是Prim算法，那么后者能不能解决这个问题呢？有种类似变形Prim的算法。

和变形Kruskal算法一样，一开始假设所有墙都存在，伪代码如下：

S = {(0,0)}
T = {}
while visited.size != n * n
  u = S.pop
  for v in neighbors(u).random_shuffle
    if component(v) != component(u)
      T << (u, v)
      S << v

最后T集合就是spanning tree中的边，即所需拆除的墙。

如果经典的Prim算法实现看作是维护了一个priority queue来维护connected component中的点，那么这里S可以用比priority queue简单的stack或queue来实现。原因是我们求的不是minimum spanning tree，所有顶点的权值可以看作是相同的；所有边的权值也可以看作是相同的。

如果用stack代替priority queue，那么我们就甚至无需显示维护一个stack了，直接使用程序函数调用时系统维护的栈。

随机选择一个顶点作为起点
对于当前点的每一个邻点，如果这个邻点和当前点不在同一个connected component，
那么就在它们之间建立一条边，即把它们之间的墙拆掉，并且递归调用该步骤，当前点设置为这个邻点。

Haskell实现

下面实现来自http://megasnippets.com/source-codes/haskell/maze_generation

import Control.Monad

import Control.Monad.ST

import Data.Array

import Data.Array.ST

import Data.STRef

import System.Random

rand :: Random a => (a, a) -> STRef s StdGen -> ST s a

rand range gen = do

(a, g) <- liftM (randomR range) $ readSTRef gen

gen `writeSTRef` g

return a

data Maze = Maze {rightWalls, belowWalls :: Array (Int, Int) Bool}

maze :: Int -> Int -> StdGen -> ST s Maze

maze width height gen = do

visited <- mazeArray False

rWalls <- mazeArray True

bWalls <- mazeArray True

gen <- newSTRef gen

liftM2 (,) (rand (0, maxX) gen) (rand (0, maxY) gen) >>=

visit gen visited rWalls bWalls

liftM2 Maze (freeze rWalls) (freeze bWalls)

where visit gen visited rWalls bWalls here = do

writeArray visited here True

let ns = neighbors here

i <- rand (0, length ns - 1) gen

forM_ (ns !! i : take i ns ++ drop (i + 1) ns) $ \there -> do

seen <- readArray visited there

unless seen $ do

removeWall here there

visit gen visited rWalls bWalls there

where removeWall (x1, y1) (x2, y2) = writeArray

(if x1 == x2 then bWalls else rWalls)

(min x1 x2, min y1 y2)

False

neighbors (x, y) =

(if x == 0 then [] else [(x - 1, y )]) ++

(if x == maxX then [] else [(x + 1, y )]) ++

(if y == 0 then [] else [(x, y - 1)]) ++

(if y == maxY then [] else [(x, y + 1)])

maxX = width - 1

maxY = height - 1

mazeArray = newArray ((0, 0), (maxX, maxY))

:: Bool -> ST s (STArray s (Int, Int) Bool)

printMaze :: Maze -> IO ()

printMaze (Maze rWalls bWalls) = do

putStrLn $ '+' : (concat $ replicate (maxX + 1) "---+")

forM_ [0 .. maxY] $ \y -> do

putStr "|"

forM_ [0 .. maxX] $ \x -> do

putStr " "

putStr $ if rWalls ! (x, y) then "|" else " "

putStrLn ""

forM_ [0 .. maxX] $ \x -> do

putStr "+"

putStr $ if bWalls ! (x, y) then "---" else " "

putStrLn "+"

where maxX = fst (snd $ bounds rWalls)

maxY = snd (snd $ bounds rWalls)

main = getStdGen >>= stToIO . maze 11 8 >>= printMaze

##include <stdbool.h>

##include <stdio.h>

##include <stdlib.h>

##include <string.h>

##define N 92

bool R[N][N], D[N][N], v[N][N];

int m, n;

void dfs(int r, int c)

int d = rand() % 4, dd = rand()%2 ? 1 : 3;

v[r][c] = true;

for (int i = 0; i < 4; i++) {

int rr = r + (int[]){-1,0,1,0}[d],

cc = c + (int[]){0,-1,0,1}[d];

if ((unsigned)rr < m && (unsigned)cc < n && ! v[rr][cc]) {

if (d % 2)

R[r][c - (d == 1)] = true;

D[r - (d == 0)][c] = true;

dfs(rr, cc);

d = (d + dd) % 4;

int main()

scanf("%d%d", &m, &n);

dfs(0, 0);

for (int c = 0; c < n; c++)

printf("._");

printf(".\n");

for (int r = 0; r < m; r++) {

printf("|");

for (int c = 0; c < n; c++) {

putchar(D[r][c] ? ' ' : '_');

putchar(R[r][c] ? '.' : '|');

printf("\n");

Eller算法(以行为单位的随机拆墙)

对于直接输出的算法来说，上述算法额外数据结构的空间复杂度都是和迷宫大小同阶的，其实我们只需要和迷宫宽(或高)同阶的额外空间就够了。

这个算法我所了解的出处是某届IOCCC的一个作品。http://homepages.cwi.nl/~tromp/maze.html给出了该作品的描述，后文我给出的实现也借鉴了链接中给出的代码。

先考虑第一行，随机拆掉一些格子的右墙。维护若干双线循环链表，每个链表表示这行连通的格子。所以拆墙后，如果第一行有x堵墙，那么就有x-1条链表。之后要决定哪些格子和下面一行相连。

._._._._._._.
|_. |_._. | |

在上图中，有2堵墙，有三个格子被决定和下面一行相连。最右边的格子没有和左边相连，但是只要它的下墙被拆除，那么它最终还是会和所有格子连通。因此这堵下墙的拆除是必需的。

接下来要处理第二行了，依旧是决定哪些格子的右墙须要被拆除。但要注意如果格子i的右墙即格子i和i+1之间的墙被拆除了，那么必须保证在上面各行格子i和i+1不连通。到这里为什么要使用链表维护连通性就明显了，我们需要快速判断格子i和i+1在当前行之前有没有连通来决定它们俩之间的墙能否被拆除，用union-find算法当然可行，但链表更方便。

在决定完拆除第二行一些格子的右墙后，考虑哪些格子需要和下一行(即第三行)相连，假设我们的决定是这样的：

._._._._._._.
|_. |_._. | |
| |_._._. . |

这里注意到第二行最左边的格子，它的右墙没有被拆除，所以它的下墙必须被拆除以保证最终它会和其他格子连通。

然后考虑第三行哪些格子的右墙要被拆除：

._._._._._._.
|_. |_._. | |
| |_._._. . |
|_._. | |_| |

注意上图第三行最后两个格子，它们之间有墙，这堵墙不能被拆除，理由是第二行时它们已经连通了。

之后几行如法炮制：

._._._._._._.
|_. |_._. | |
| |_._._. . |
|_._. | |_| |
|_._._. | | |
| | ._._. | |
| |_._._| ._|

然后开始处理最后一行。最后一行的任务有点特殊，因为下墙不能被拆除(迷宫边界)，需要拆除若干右墙使得最后一行的几个连通分支并在一起。发现不得不写成这样：

._._._._._._.
|_. |_._. | |
| |_._._. . |
|_._. | |_| |
|_._._. | | |
| | ._._. | |
| |_._._| ._|
|_._._._._._|

Disjoin-set forest的删除元素操作

之前的例子中我们发现每一行我们做了两步决策，拆右墙和拆下墙。有些时候右墙不能被拆除，是因为墙两边的格子在之前行已经被连通了。拆右墙就相当于合并两个集合。

右墙决策产生之后，有些下墙是必须拆的，即当它自成一个集合时。如果不拆下墙，那么在下一行，这个格子就和其他不连通了，所以得自成一个集合。

推敲我们需要实现的操作：并、查、从集合中删除一个元素，如果只有连两个操作，那么很简单，直接套用 disjoin-set forest 就好了。难点就在于如何支持“从集合中删除一个元素”这一操作。删除其实也是更新，引入时间因素后，就可以用一条更新记录来代替一个删除操作，但要注意把被删除的记录置为无效状态。删除一个元素，可以看作：引入一个新顶点，改变格子指向顶点的映射。

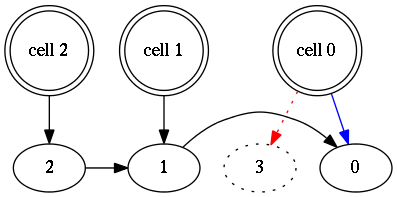
删除元素

如图，在格子0删除下墙前没有虚线边以及虚线顶点3。删除格子0的下墙后，需要让格子0对应的元素(顶点0)自成一个集合。做法是把蓝线(格子指向顶点的映射)换成红色虚线。尽管有顶点1和2在disjoin-set forest中已经指向顶点3，但是我们做的这个删除操作不会影响到它们。

用linked list实现disjoin sets

上一节通过改造disjoin-set forest使其支持删除元素的操作，但是改造后空间复杂度就没有吸引力了，因为所有产生的顶点数目可能是迷宫大小级别。

仔细研究我们用到的操作：

合并：只有相邻格子所对应集合会合并；
比较两个格子是否在一个集合中：只有相邻格子会被比较。

用一个链表表示一个connected component，并且让链表的元素按编号排序。那么对于格子i，查找其对应的链表中节点的后继是否对应格子i+1就能知道格子i和i+1是否在同一个connected component。对于合并操作，以及让一个格子自成一个集合的操作，链表也都能出色地完成任务。

._._._._._._.
|_. |_._. | |

行间有两堵墙，需要三个链表：

L[0] = 1, L[1] = 0; R[0] = 1, R[1] = 0
L[2] = 4, L[3] = 2, L[4] = 3; R[2] = 3, R[3] = 4, R[4] = 2
L[5] = 5; R[5] = 5

现在考虑第二行，上面的链表状态代表的迷宫如下：

._._._._._._.
|_. |_._. | |
| | | | | | |

决定拆除一些墙后：

._._._._._._.
|_. |_._. | |
| | . . . . |

相应地，链表状态变成：

L[0] = 0; R[0] = 0
L[1] = 5, L[2] = 1, L[3] = 2, L[4] = 3, L[5] = 4; R[1] = 2, R[2] = 3, R[3] = 4, R[4] = 5, R[5] = 1

接着决定拆掉一些下墙：

._._._._._._.
|_. |_._. | |
| |_._._. . |

那么格子1 、2、3都得自成一个集合，链表状态变成：

L[0] = 0; R[0] = 0
L[1] = 1; R[1] = 2
L[2] = 2; R[2] = 2
L[3] = 3; R[3] = 3
L[4] = 5, L[5] = 4; R[4] = 5, R[5] = 4

目前第三行尚未考虑拆墙，由上面的链表状态得出的连通信息：格子0、1、2、3互不连通，格子4、5连通，恰好能反应下图：

._._._._._._.
|_. |_._. | |
| |_._._. . |
| | | | | | |

OCaml实现

let eller m n =

let l = Array.create (n+1) 0 in

let r = Array.create (n+1) 0 in

for i = 0 to n-1 do

print_string "._";

l.(i) <- i;

r.(i) <- i

done;

l.(n) <- n-1;

print_string ".\n|";

for y = 0 to m-2 do

for x = 0 to n-1 do

let w = l.(x+1) in

let pat1 =

if x <> w && Random.int 3 <> 0 then begin

r.(w) <- r.(x);

l.(r.(w)) <- w;

r.(x) <- x+1;

l.(x+1) <- x;

end else

let pat0 =

if x <> l.(x) && Random.int 3 <> 0 then begin

l.(r.(x)) <- l.(x);

r.(l.(x)) <- r.(x);

l.(x) <- x;

r.(x) <- x;

end else

print_char pat0;

print_char pat1

done;

print_string "\n|"

done;

for x = 0 to n-1 do

let w = l.(x+1) in

let pat1 =

if x <> w && (x == l.(x) || Random.int 3 <> 0) then begin

r.(w) <- r.(x);

l.(r.(w)) <- w;

r.(x) <- x+1;

l.(x+1) <- x;

end else

l.(r.(x)) <- l.(x);

r.(l.(x)) <- r.(x);

l.(x) <- x;

r.(x) <- x;

print_char '_';

print_char pat1

done;;

Scanf.scanf "%d %d" eller

##include <stdio.h>

##include <stdlib.h>

##define N 92

int L[N], R[N];

int main()

char pat[3] = {};

int m, n;

scanf("%d%d", &m, &n);

for (int i = 0; i < n; i++) {

printf("._");

L[i] = R[i] = i;

L[n] = n - 1;

printf(".\n|");

while (m--) {

for (int i = 0; i < n; i++) {

int j = L[i + 1];

if (i != j && rand() % 3) {

L[R[j] = R[i]] = j;

L[R[i] = i + 1] = i;

pat[1] = '.';

} else

pat[1] = '|';

if (i != L[i] && rand() % 3) {

L[R[i]] = L[i];

R[L[i]] = R[i];

L[i] = R[i] = i;

pat[0] = '_';

} else

pat[0] = ' ';

printf(pat);

printf("\n|");

pat[0] = '_';

for (int i = 0; i < n; i++) {

int j = L[i + 1];

if (i != j && (i == L[i] || rand() % 3)) {

L[R[j] = R[i]] = j;

L[R[i] = i + 1] = i;

pat[1] = '.';

} else

pat[1] = '|';

L[R[i]] = L[i];

R[L[i]] = R[i];

L[i] = R[i] = i;

printf(pat);

Maze Generation: Eller’s Algorithm给出了关于Eller算法的详细描述。

Maze Classification给出了非常详细的迷宫生成算法和解法列表。

Perfect maze

变形Kruskal算法

Aldous-Broder算法

Haskell实现

Recursive backtracking算法

Haskell实现

Eller算法(以行为单位的随机拆墙)

Disjoin-set forest的删除元素操作

用linked list实现disjoin sets

OCaml实现

Recommend

DEFCON 25 CTF参赛记

使用cquery：C++ language server

Android微信数据导出

ImagePy解析：23 -- ROI操作

(转载)Harris角点检测原理

wxPython知识点

胞状物体通用分割算法Cellpose解析：开发篇

如何编写一个简单地内核模块

如何实现进程代码段的分页度量

线段树笔记

About Joyk