

内功修炼-线段树(一) | Redmaple1的博客
source link: http://redmapleren.com/2020/03/30/%E5%86%85%E5%8A%9F%E4%BF%AE%E7%82%BC-%E7%BA%BF%E6%AE%B5%E6%A0%91%EF%BC%88%E4%B8%80%EF%BC%89/?
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

前一阵子朋友换工作,去了新公司的一个基础服务的部门。对数据结构和算法的要求着实不低,不是平常的CRUD,而是通过各种巧妙的数据结构去完成对应的业务需求。我发现是时候夯实一下基础了,这次来看一下树结构中的线段树。
一、什么是线段树
有一种很经典的线段树问题:区间染色。
讲的是有一面长度为 n 的墙,每次选择一段儿墙进行染色。
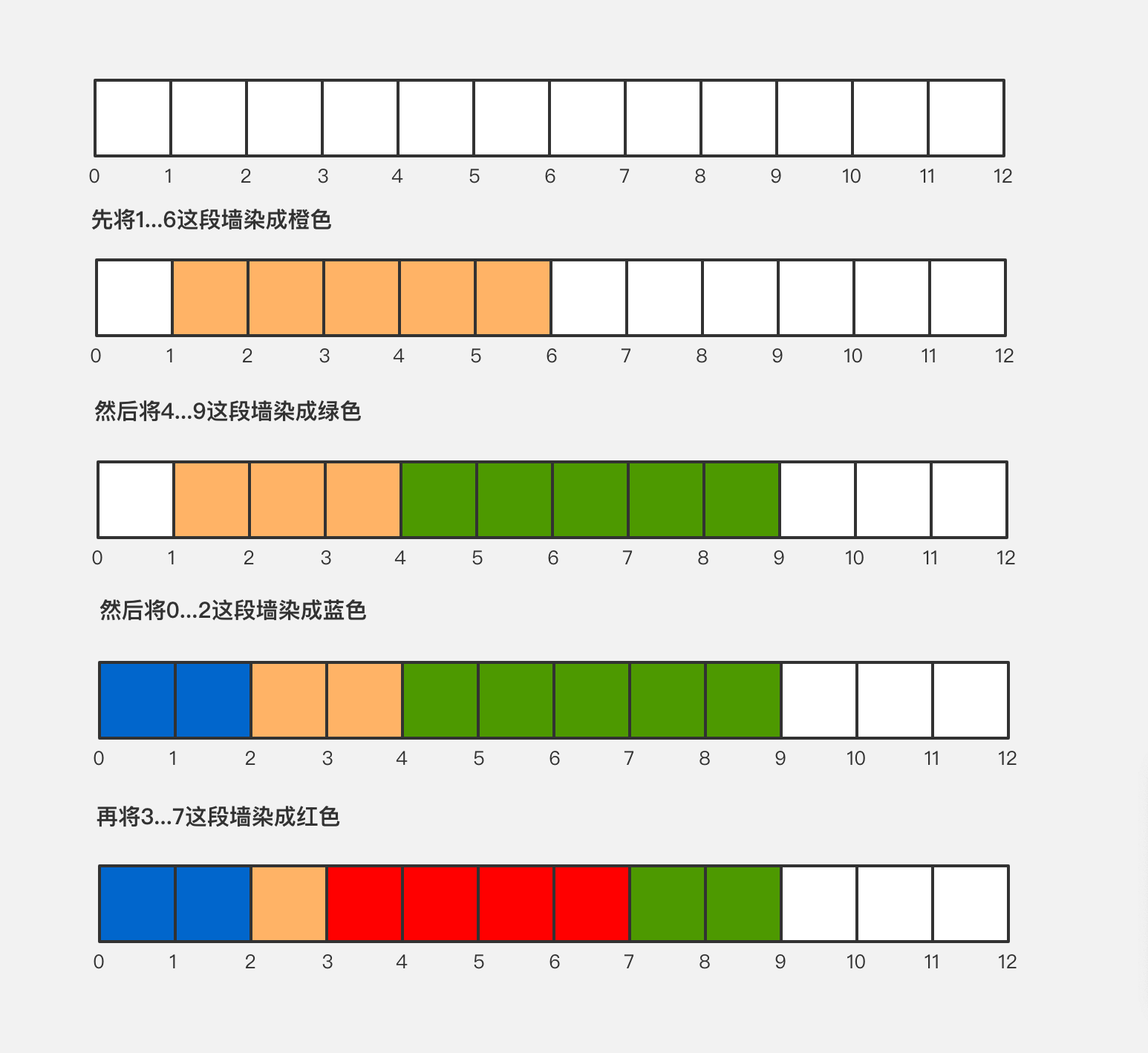
在染色的过程中,会有一部分被重复染色,那么 m 次操作后,我们可以看见多少种颜色呢?在 [i,j] 区间内可以看见多少种颜色呢?
我们可以知道上述的问题是对区间进行以下的操作:
- 更新区间(染色操作)
- 查询区间(查询操作)
通过上面的图片描述,我们很容易可以想到利用数组来实现,对于染色操作和查询操作时间复杂度均是是 O(n)。
其实更普遍一点,这一类问题的实质,是基于区间的统计查询。比如一个电商网站,需要看2019年的注册用户消费额最高的用户。这里需要注意,我们关注的是动态的情况,是看在2019年注册的用户在到现在为止消费额的统计量,并不是说在单单在2019年消费最高的。如果是单单2019年消费最高的统计,直接拿出2019年的数据进行统计即可,因为2019年的数据已经是定值了。我们考虑的是动态的情况,是伴随更新的同时进行查询,即既有更新又有查询的操作,此时,使用线段树是一种好的选择。当然依然可以使用普通数组进行实现,只不过使用线段树的时间复杂度会低一些。
| 使用数组实现 | 使用线段树 | |
|---|---|---|
| 更新 | O(n) | O(logn) |
| 查询 | O(n) | O(logn) |
我们总结以上讨论的问题场景:
对于给定的区间,支持以下两种操作。
更新: 更新区间中一个元素或者一个区间的值
查询一个区间 [i,j] 的最大值、最小值,或者区间数字和等。
那么我们怎么抽象出线段树的数据结构呢?
通过上面的说明,我们是不会像线段树中进行添加和删除元素的,即区间的长度是固定不变的,只是区间中的元素可能会发生变化。所以我们可以使用一个静态数组来表示,线段树具体就是下面的样子。
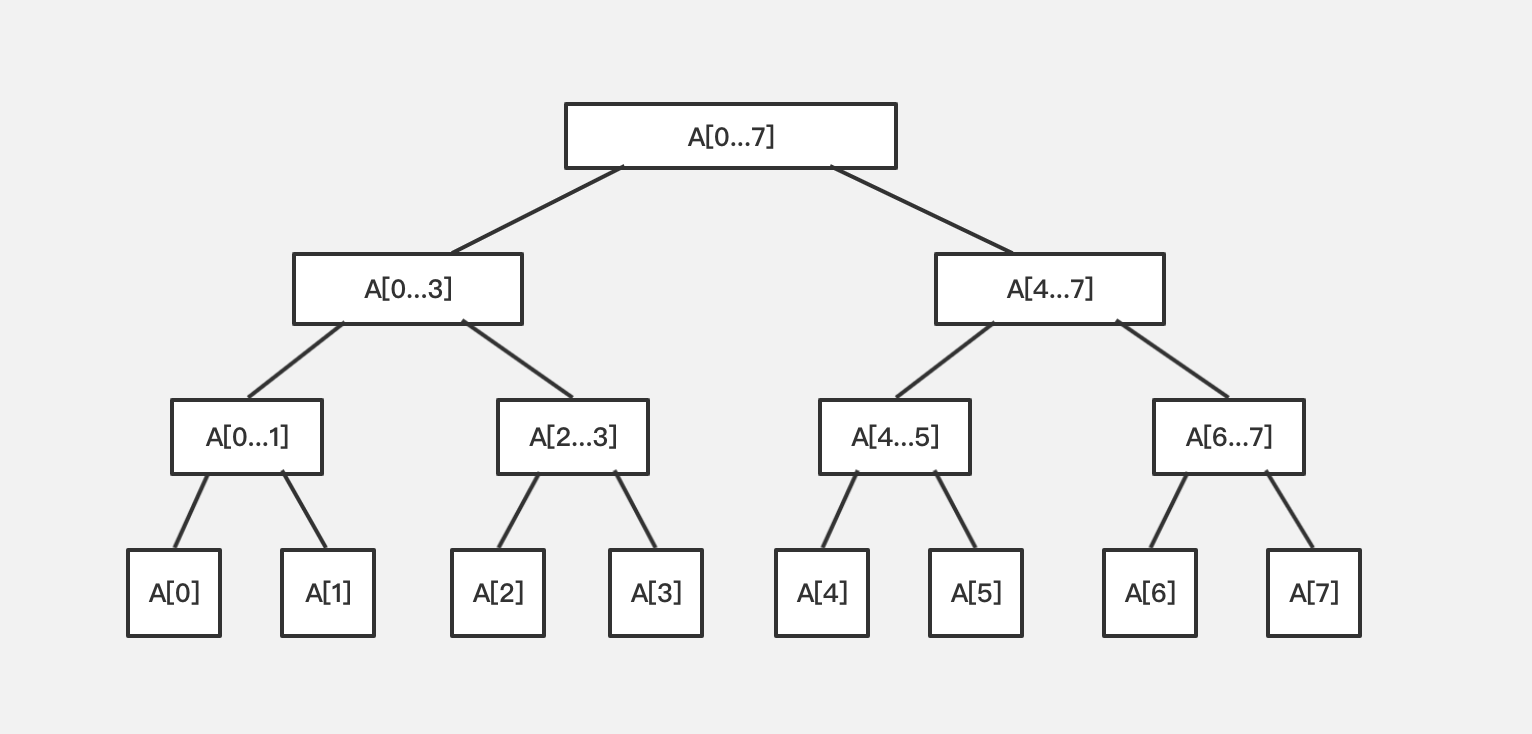
和普通二叉树的区别是,每一个节点所表示的是一个区间内的信息。以求合为例,每一个节点存储的是每个区间相应的数字和,根节点是整个区间的数字和,之后往下分成两个子区间,以此类推,直到最后叶子节点是单个的数字。
当我们需要求[4…7]区间的和,可以很方便的从树中找到,并不需要对数组进行挨个遍历。
二、线段树的表示
在上面线段树有8个叶子节点,比较特殊,正好是一个满的二叉树,如果有10个元素,线段树是下面的情况:
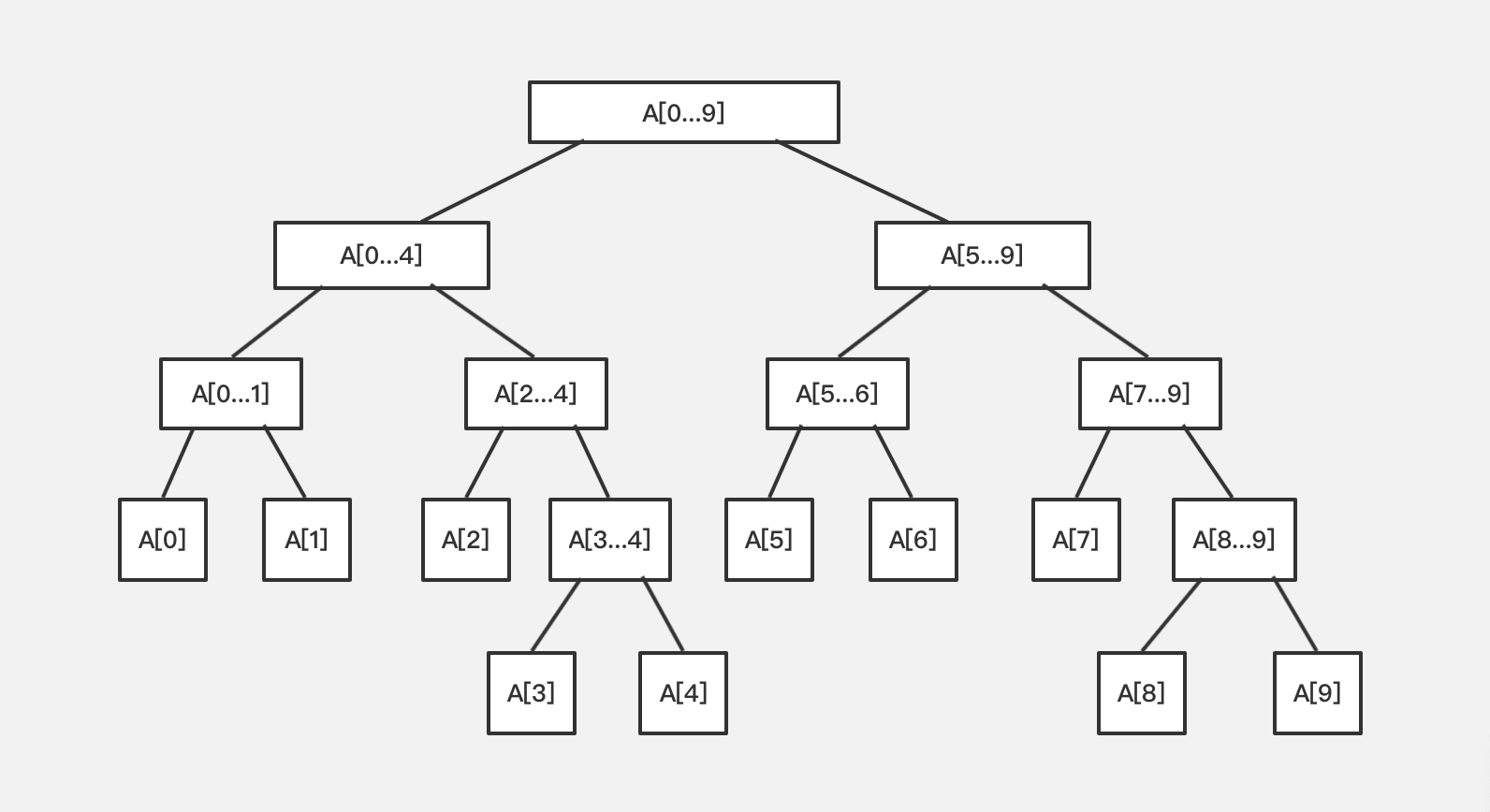
当一个节点不能平均分的时候,这里把这个节点分成一个节点少一点,一个节点多一点。
所以,线段树不是完全二叉树,但是是平衡二叉树。
为了简便,其实我们可以把线段树看作是一棵满的二叉树,只不过最后一层的叶子点有些是空的。满的二叉树我们可以很方便的用数组来表示,那么问题来了,我们需要多少节点来表示这课树呢?
根据满二叉树的节点规律,我们可以看到每一层的节点和层数是有如下的关系的:
- 3层:4
… - h-1层:2^(h-1)
根据等比数列求合公式,可得出,对满二叉树,h 层,一共有 2^h - 1 个节点,大约是 2^h,这里富裕一个节点,肯定可以放下 2^h - 1 个节点。
最后一层(h-1层),有 2^(h-1) 个节点。
可以看到,最后一层的节点数大致等于前面所有层节点之和。
有了上面的结论,如果区间有 n 个元素,用数组描述线段树需要有多少节点呢?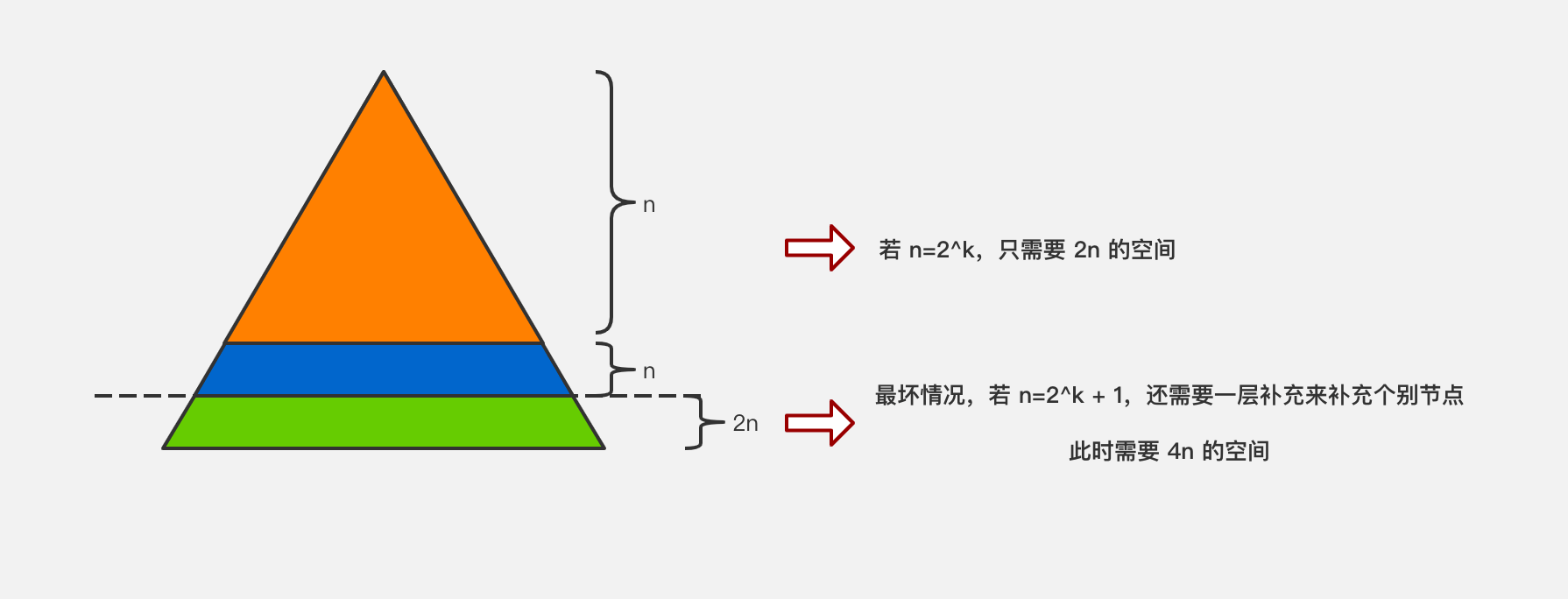
通过上面的推导,如果区间有 n 个元素,需要 4n 的空间来存储整个线段树。由于我们不考虑添加元素,即区间是固定的,所以使用 4n 的静态空间即可。
当然 4n 是一个估计值,这 4n 的空间并不是都被占满的,我们留有空余。比如下图的情况,最后一层大部分的节点是 null。
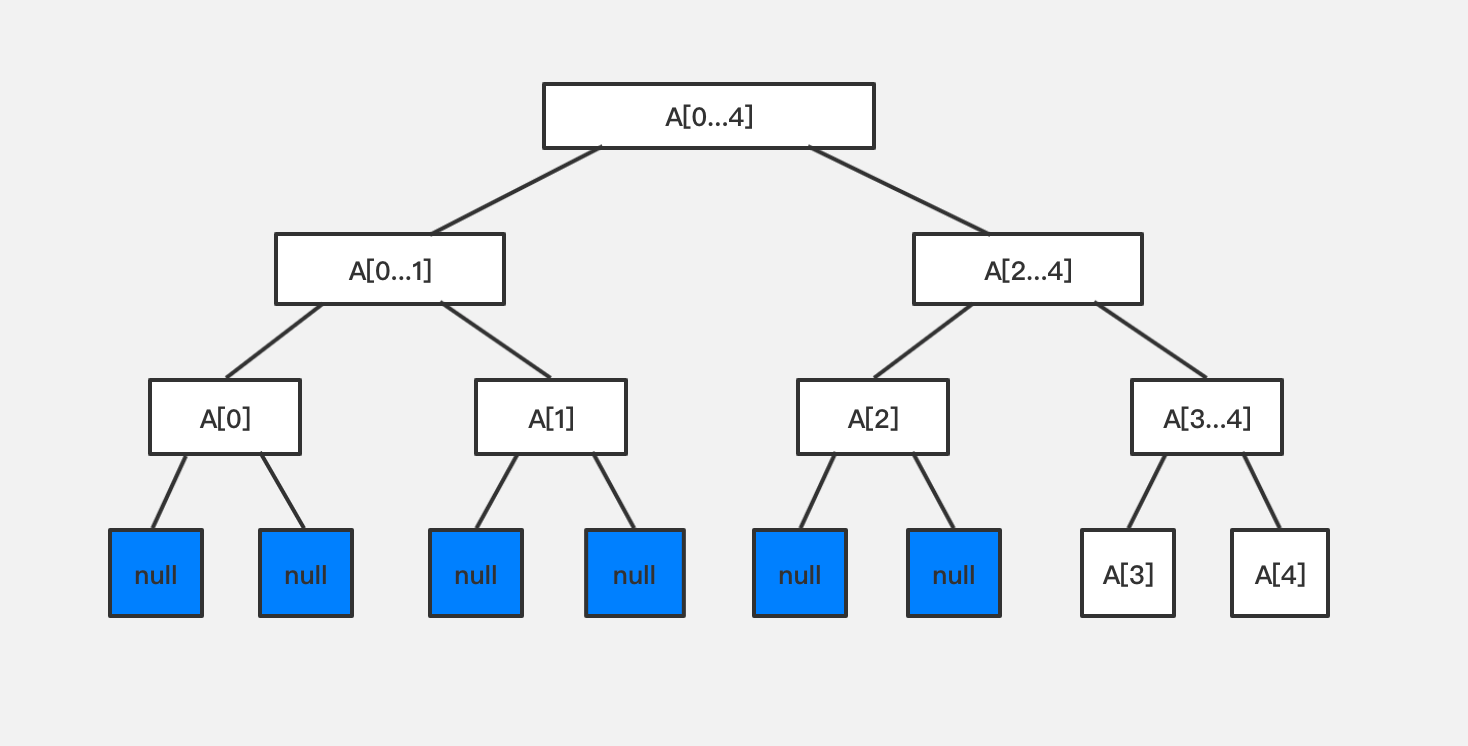
我们暂不考虑这种浪费的问题。对于现代计算机来说,多出来的这些节点基本是不影响空间的,这里就是算法的空间换时间的体现。
三、创建线段树
有了上面的分析,具体的代码实现其实很简单。data 是存储元素的数组,tree 是树结构使用的数组。
1 | public class SegmentTree<E> { |
下面具体分析一下如何 build 线段树的节点。
我们利用树的递归结构来创建,treeIndex 表示正在创建的线段树的根节点的索引,l 表示区间的左边界,r 表示区间的右边界。递归终止的条件就是当左边界等于右边界(l == r)时,这时要构建的树 tree[treeIndex] 就是 元素数组对应的索引的值(data[l] 或 data[r])。之后找到当前线段树的左右子树的根节点索引和索引中间值 mid,接下来就是递归调用该方法,先创建左子树,后创建右子树,之后合并两棵子树得到正在创建的树的根节点数据。代码如下:
1 | /** |
代码中的 merger 是对于合并这个操作的抽象,因为我们的线段树结构是一个通用的结构,不可能仅支持求合或求积的操作,这里就利用 java 的多态性,使用接口来抽象这个合并操作。具体的业务可以通过实现这个接口来实现自己的逻辑。
public interface Merger<E> {
E merge(E a, E b);
}
以上,我们就完成了线段树的创建。
在下篇文章中,我们将看如何在线段树中进行查询和更新操作。
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK